
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Бесконечно большие функции и их связь с бесконечно малыми функциями
Функция F(x) называется бесконечно большой (сокращенно б.б.) при x → +∞ Функция F(x) называется бесконечно большой при x → x0 (при x → x0–0 или Очевидно, что всякая бесконечно большая функция не является ограниченной при Если F (x) – б.б. функция при x → a, то говорят, что F (x) стремится к бесконечности и пишут: Пример 1. F1(x) = x2 является б.б. при x → +∞ и x → -∞, причем F1(x) > 0, поэтому можно записать: Следующие две теоремы устанавливают связь между бесконечно большими и бесконечно малыми функциями. Теорема 1. Если функция F(x) является б.б при x → a, то функция Теорема 2. Если a(x) – б.м. при x → a и a(x) ≠ 0, то Свойство 1. Если F1(x), F2(x) – б.б. при x → a, то функция F1(x), F2(x) – б.б. при x → a. Свойство 2. Если F1(x), F2(x) – б.б. функции при x→a, причем F1(x) > 0 и Свойство 3. Если F(x) – б.б. при x → a и число C≠ 0, то CF(x) – б.б. при x → a. Замечание. Если F1(x) и F2(x) – б.б. функции при x → a, но имеют разные знаки, то F1(x) + F2(x) может быть как б.б., так и б.м. при x → a, как иметь предел при x → a, так и не иметь его.
Основные теоремы о пределах Теорема 1. Если Теорема 2. Если функцию f(x) можно представить в виде: f (x) = b + a(x), где b – число, a(x) – б.м. функция при x → a, то Теорема 3. Предел суммы (разности) двух функций равен сумме (разности) их пределов, т.е. если Теорема 4. Предел произведения двух функций равен произведению их пределов, т.е. если Следствие 2. Если n – натуральное число, то Теорема 5. Предел дроби равен пределу числителя, деленному на предел знаменателя при условии, что предел знаменателя не равен нулю. Иначе, если
Пример. Найти Теорема 6. Если Теорема 8. (теорема о сжатой переменной). Если
Первый замечательный предел Рассмотрим функцию Второй замечательный предел Рассмотрим возрастающую последовательность: a1,a2,...,an,... Для нее an+1>an для любого натурального n. Если эта последовательность не является ограниченной, то она не имеет предела, так как ее члены неограниченно возрастают. Если же возрастающая последовательность ограничена, то она имеет предел. Этот факт доказывается в полных курсах математического анализа [6], мы приведем лишь его полную формулировку.
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 746; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.173.112 (0.006 с.) |

 не существует.
не существует. Если при этом F (x) > 0, то пишут:
Если при этом F (x) > 0, то пишут:  ; если же F(x) < 0, то пишут:
; если же F(x) < 0, то пишут:  .
.
 является б.б. при x → 0, причем
является б.б. при x → 0, причем 
 – б.м. при x → a.
– б.м. при x → a. – б.б. при x → a.
– б.б. при x → a. ), то функция F1(x) + F2(x) – б.б. при x → a.
), то функция F1(x) + F2(x) – б.б. при x → a. , где a(x) – б.м. при x → a.
, где a(x) – б.м. при x → a. .
.
 .
. 
 .
.

 .
.  . Аналогично,
. Аналогично,  Используя теорему 5, получим:
Используя теорему 5, получим: 
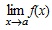 существует и f(x) ≥ 0 для всех x из области определения функции, то
существует и f(x) ≥ 0 для всех x из области определения функции, то 
 существуют, то
существуют, то 
 и
и 
 , аргумент x (как всегда в математическом анализе) выражается в радианах. При x = 0 функция
, аргумент x (как всегда в математическом анализе) выражается в радианах. При x = 0 функция  не определена.
не определена. 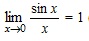 (первый замечательный предел).
(первый замечательный предел). 


