Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отбор фактора в модель парной регрессии
Фактор, который будет использован в парной модели, должен отвечать следующим требованиям: его влияние на результат должно быть таким, что влиянием всех остальных факторов можно пренебречь, но он не должен находиться в функциональной зависимости с результатом. Число наблюдений фактора
Спецификация модели парной регрессии В парной регрессии используют линейные и нелинейные функции: · · · · · · Выбор вида функции в модели парной регрессии может быть осуществлен следующими методами: 1. Графический метод. В его основу положено построение и исследование графика «корреляционное поле», на основании которого делается вывод о виде функции описывающей взаимосвязь между явлениями. 2. Аналитический метод. Опирается на изучение природы взаимосвязи между исследуемыми явлениями. 3. Экспериментальный метод. Вид функции подбирается экспериментально через анализ качества подбора функции, путем сравнения остаточной дисперсии рассчитанной для разных моделей. Парная линейная регрессия
Парная линейная регрессия наиболее часто применяется в регрессионных моделях, в силу простоты расчета и интерпретирования результатов. Расчет регрессионной модели данного вида заключается в нахождении уравнения вида:
или где;
Показывает влияние не учтенных в модели факторов, а также случайных ошибок.
Решение уравнения регрессии заключается в расчете его параметров. Наибольшее распространение из методов расчета параметров уравнения получил метод наименьших квадратов (МНК). МНК позволяет получать такие значения
При расчете параметров уравнения при помощи МНК необходимо решить систему из двух нормальных уравнений.
Также используют и готовые уравнения. Для расчета параметра
где:
Для расчета параметра
Параметр Параметр
где Геометрически это тангенс угла наклона прямой регрессии
Пример 7. Имеются данные о средней прибыли Построить линейное уравнение регрессии. Таблица 21.
Решение. Для расчета параметров уравнения регрессии
1. Рассчитаем, в таблице 22, все возможные значения и подставим в систему. После подстановки данных получим систему:
1) Решим систему методом исключения параметра
Далее из второго уравнения вычтем первое
Рассчитаем коэффициент регрессии:
Подставим значение
Таблица 22
2. Рассчитаем параметры уравнения
Небольшие расхождения в расчете параметров Подставим полученные значения (возьмем значения полученные в Microsoft Excel, как наиболее точные. см. далее) в уравнение регрессии
Коэффициент парной линейной регрессии Далее подставляя значения фактора
2) Рассмотрим решение данной задачи в Microsoft Excel. Первое. В новой книге Microsoft Excel внесем исходные данные (рис 1).
Рисунок 1. Далее нажимаем кнопку Сервис и в открывшейся панели нажимаем кнопку Анализ данных. В панели Анализ данных нажимаем Регрессия: В панели регрессия вводим входной интервал
Рисунок 2. Нажимаем ОК. Появится таблица, содержащая результаты регрессионного анализа (рис 3).
Рисунок 3. Параметр Парная линейная корреляция
Простейшим методом определения наличия и формы взаимосвязи является построения корреляционной таблицы и графика «корреляционное поле». Корреляционная таблица – таблица, в которой записываются частоты сочетаний результативного и факторного показателей. В настоящее время корреляционная таблица не используется для вычисления уравнения связи. Пример 8. Имеются данные о себестоимости единицы продукции Таблица 23.
Составим корреляционную таблицу (табл. 24). Таблица 24.
По корреляционной таблице можно сделать следующие выводы. Если
Корреляционное поле (графический метод изучения взаимосвязей) – точечный график, характеризующий единицу наблюдения по двум признакам. Факторный признак откладывается по оси абсцисс, результативный признак по оси ординат. По данным примера 8 построим корреляционное поле (рис. 4).
Рисунок 4 Анализ корреляционного поля показывает, что имеется прямая связь. Если связь между признаками обратная, то корреляционное поле будет иметь примерно такой вид (рис. 5).
Рисунок 5 Если корреляционное поле имеет следующий вид (рис. 6) можно сделать вывод об отсутствии выраженной взаимосвязи.
Рисунок 6 Корреляционная таблица и корреляционное поле показывают лишь наличие, отсутствие и направление связи. Но они не дают представления о тесноте, интенсивности связи между признаками. Тесноту связи в парной линейной модели определяют, рассчитывая линейный коэффициент парной корреляции
или где:
где
Коэффициент корреляции также можно рассчитать через значение признаков в стандартизованном масштабе:
где:
Коэффициент корреляции может принимать значения от · меньше 0,3 (-0,3) - связь положительная (отрицательная) слабая; · от 0,3 до 0,7 (от -0,3 до -0,7) - связь положительная (отрицательная) средняя; · свыше 0,7 (-0,7) - связь положительная (отрицательная) сильная; · равен 1 (-1) - связь функциональная положительная (отрицательная); · равен 0 – связь отсутствует.
Другой показатель тесноты связи – коэффициент парной детерминации. Он показывает часть вариации результативного признака, которая сложилась под влиянием включенного в парную модель фактора. Коэффициент парной детерминации
Коэффициент парной детерминации позволяет определять тесноту связи не только в линейных, но и в нелинейных моделях. Коэффициент парной детерминации может принимать значения от
Пример 9. Имеются данные о средней прибыли Таблица 25.
Рассчитать коэффициент парной линейной корреляции Решение. 1) Так, как из примера 7 известно, что уравнение регрессии
Коэффициент парной корреляции Возведя коэффициент корреляции в квадрат, получим коэффициент детерминации.
Коэффициент детерминации показывает, что 52% от всей вариации результативного признака обусловлено влиянием включенного в модель фактора, а 48% вариации вызвано влиянием всех остальных, не исследуемых в данной модели факторами.
2) Рассмотрим решение данной задачи в Microsoft Excel. В новой книге Microsoft Excel внесем исходные данные (рис 7). Далее нажимаем кнопку Сервис и в открывшийся панели нажимаем кнопку Анализ данных В панели Анализ данных нажимаем корреляция: В панели корреляция вводим входной интервал, выделяя все столбики, содержащий и данные результативного признака и данные фактора. Ответ можно поместить на новом рабочем листе, в новой рабочей книге, или на листе, содержащем условия выбирая выходной интервал, для чего указываем графа-клетку начала размещения ответа (рис. 7).
Рисунок 7. Нажимаем ОК. Появится таблица парных линейных коэффициентов корреляции (рис. 8).
Рисунок 8. На пересечении столбца 1 и столбца 2 и будет искомый коэффициент парной линейной корреляции.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 529; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.89.85 (0.07 с.) |
 должно превышать число параметров при переменной
должно превышать число параметров при переменной  необходимо не менее 6-7 наблюдений, а для модели
необходимо не менее 6-7 наблюдений, а для модели  потребуется не менее 12-14 наблюдений.
потребуется не менее 12-14 наблюдений. – линейная функция
– линейная функция – полином второй степени
– полином второй степени – полином третьей степени и т.д.
– полином третьей степени и т.д. – равносторонняя гипербола
– равносторонняя гипербола – степенная функция
– степенная функция – показательная функция и т.д.
– показательная функция и т.д. (30)
(30) - теоретическое значение результативного признака, рассчитанное по уравнению регрессии, показывающему взаимосвязь между
- теоретическое значение результативного признака, рассчитанное по уравнению регрессии, показывающему взаимосвязь между 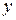 и
и 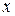 .
. - случайная величина (возмущение, шум)
- случайная величина (возмущение, шум) (31)
(31) - параметры уравнения.
- параметры уравнения. .
. (32)
(32) (33)
(33) :
: ; так как
; так как 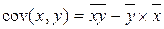 получим:
получим: или
или  (34)
(34) (35)
(35) (36)
(36) :
: (37)
(37) и только в этом случае имеет экономический смысл, если
и только в этом случае имеет экономический смысл, если  параметр
параметр  с осью ординат.
с осью ординат.
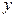 прибыль млн. руб. в месяц, а
прибыль млн. руб. в месяц, а 



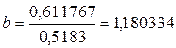 .
.






 , используя готовые уравнения.
, используя готовые уравнения.


 показывает, что при увеличении фактора – «затраты на рекламу» на 1 единицу (1 млн. руб.), результат – «средняя прибыль» увеличится, в среднем на 1,180332 млн. руб.
показывает, что при увеличении фактора – «затраты на рекламу» на 1 единицу (1 млн. руб.), результат – «средняя прибыль» увеличится, в среднем на 1,180332 млн. руб.


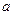 в данной таблице находится на пересечении столбика «Коэффициенты» и строки «Y-пересечение», параметр
в данной таблице находится на пересечении столбика «Коэффициенты» и строки «Y-пересечение», параметр 




 или просто коэффициент корреляции. Существуют формулы расчета:
или просто коэффициент корреляции. Существуют формулы расчета: (38)
(38) (39)
(39) - среднее квадратическое значение факторного признака;
- среднее квадратическое значение факторного признака;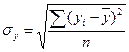 - среднее квадратическое значение результативного признака;
- среднее квадратическое значение результативного признака; (40)
(40) - сумма квадратов отклонений обусловленная влиянием фактора
- сумма квадратов отклонений обусловленная влиянием фактора  - общая сумма квадратов отклонений признака
- общая сумма квадратов отклонений признака  (41)
(41) – значения признаков в стандартизованном масштабе.
– значения признаков в стандартизованном масштабе.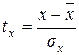 (42)
(42) (43)
(43) до
до  . В статистике говорят, что если значения коэффициента парной корреляции:
. В статистике говорят, что если значения коэффициента парной корреляции: рассчитывают, возводя в квадрат коэффициент парной корреляции
рассчитывают, возводя в квадрат коэффициент парной корреляции  (44)
(44) до
до 
 показывает, что между исследуемыми признаками существует тесная положительная связь.
показывает, что между исследуемыми признаками существует тесная положительная связь.