
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача восстановления функции по её производным
Основной задачей дифференциального исчисления является отыскание производной заданной функции. Разнообразные задачи математического анализа и его многочисленные приложения в геометрии, физике, технике приводят к обратной задаче: по данной функции f (x) найти функцию F (x), производная которой равна f (x). Определение. Функция F (x) называется первообразной для функции f (x) на некотором множестве X, если для всех значений x Î X справедливо равенство: F '(x) = f (x). Пример №1. Функция F(x) = sin x есть первообразная для функции Пример №2. Функция F (x) = x 3 есть первообразная для функции Пример №3. Функция
Задача отыскания по данной функции f (x) её первообразной F (x) решаются неоднозначно. Действительно, если F (x) – первообразная для функции f (x), т.е. F' (x) =f (x), то и функция F (x) +С, где С – произвольная постоянная, также является первообразной для функции f (x), так как производная постоянной равна нулю, и Пример. Для функции Теорема. Всякие две первообразные одной и той же функции отличаются друг от друга на постоянную, определённую на одном и том же множестве X. Доказательство 1) Пусть F1 (x) и F2 (x) – некоторые первообразные функции f (x), определенные на промежутке X. 2) Введем вспомогательную функцию Ψ(x) = F2 (x)- F1 (x), и Ψ(x) – дифференцируема на X как производная разности двух дифференцируемых функций. 3) Причем, Ψ 4) На основании следствия к теореме Лагранжа функция Ψ(x) будет являться постоянной, так как её производная равна нулю на X, следовательно, Ψ(x) =C. 5) Поэтому Ψ(x) можно представить в виде Ψ(x) = F2 (x) - F1 (x) = C, следовательно, F2 (x) = F1 (x) + C. ч.т.д. Следствие. Если F (x) – какая-либо первообразная функции f (x)на промежутке X, то совокупность всех первообразных функции f (x)на промежутке X совпадает со множеством функции { F (x) +C }, C Î ℝ, C – const. Множество первообразных функции { F (x) +C } обозначается F (x) +C, C – const. Чтобы выделить определенную первообразную Ф (x) для f (x)из { F (x) +C }, необходимо наложить некоторое дополнительное условие на функцию Ф (x). Обычно это начальное условие, т.е. требование, чтобы функция Ф (x) имела в какой-либо фиксированной точке x0 наперед заданное значение y0:
F (x0) +C = Ф (x0) + y0.
Неопределенный интеграл Равенство F' (x) = f (x) можно записать
Определение №1. Если функция F (x) –первообразная функции f (x) на промежутке X, то множество функции F (x) +C, где C – произвольная постоянная, называется неопределенным интегралом от функции f (x)на этом промежутке X и обозначается символом Символ Определение №2. Восстановлением функции по её производной или, что то же, отыскание неопределенного интеграла по данной подынтегральной функции, называется интегрированием этой функции. Интегрирование представляет собой операцию обратную дифференцированию. Для того, чтобы проверить, правильно ли выполнено интегрирование, достаточно, продифференцировать результат и получить при этом подынтегральную функцию. Пример №1. Пример №2.
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 1927; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.137.218 (0.005 с.) |
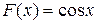 , так как " x Î ℝ: (sin x)'x = cos x.
, так как " x Î ℝ: (sin x)'x = cos x. .
. есть первообразная для функции
есть первообразная для функции  , на интервале (-1;1), так как в любой точке этого интервала
, на интервале (-1;1), так как в любой точке этого интервала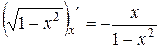 .
.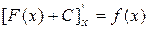 для любого числа С.
для любого числа С. первообразной является не только sin
первообразной является не только sin  , но и функция
, но и функция  , так как
, так как  .
.
 .
.
 имеет место тогда и только тогда, когда dF (x) = f (x) dx. Поэтому первообразную функции f (x) называют первообразной дифференциальной формы,
имеет место тогда и только тогда, когда dF (x) = f (x) dx. Поэтому первообразную функции f (x) называют первообразной дифференциальной формы,  , т.е.
, т.е. .
. = F (x) +C (читают: интеграл эф икс дэ икс), где f (x) – подынтегральная функция, f (x) dx – подынтегральное выражение, x – переменная интегрирования, C – постоянная интегрирования.
= F (x) +C (читают: интеграл эф икс дэ икс), где f (x) – подынтегральная функция, f (x) dx – подынтегральное выражение, x – переменная интегрирования, C – постоянная интегрирования. =
=  , неопределенный интеграл
, неопределенный интеграл 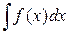 можно записать в других эквивалентных формах
можно записать в других эквивалентных формах  .
. . Утверждение верно на любом промежутке из
. Утверждение верно на любом промежутке из 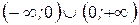 .
. , верно на любом промежутке из
, верно на любом промежутке из 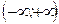 .
.


