
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предел суммы, произведение и частного функций, имеющих предел в точкеСтр 1 из 2Следующая ⇒
Теорема. Если существуют конечные пределы
причем они соответственно равны:
Доказательство 1. Эта теорема доказывается при помощи соответствующих утверждений относительно последовательностей и на основании определения предела функции в точке по Гейне. 2. Пусть 3. Соответствующие последовательности значений функций будут иметь вид 4. В силу теоремы о пределе суммы, произведения, частного двух сходящихся последовательностей
5. Тогда согласно определению предела функции в точке по Гейне существуют и конечные пределы в точке у функций соответственно:
ч.т.д. Следствие №1. Если существует предел функции Следствие №2. Предел сложной функции (замена переменных для пределов функций)
Теорема. Пусть существуют конечные (или бесконечные) пределы функции Доказательство 1. Из условий теоремы следует, что существуют такие проколотые окрестности 2. Так как 3. Следовательно, значения функции 4. Последнее утверждение можно записать 5. Возьмем произвольную последовательность значения аргумента 6. Тогда соответствующая последовательность значений функций будет иметь вид: 7. Так как по условию теоремы
8. Так как предел функции 9. Последнюю запись можно представить так:
10. Так как для произвольной последовательности значений аргумента ч.т.д. Неравенство Лемма. При любом действительном Доказательство I. 1. Рассмотрим окружность радиуса 2. Пусть радиус
3. Опустим из точки 4. Тогда 5. Проведем радиус 6. Тогда 7. Известно из курса школьной геометрии, что длина дуги окружности равна 8. Поэтому длина дуги 9. Очевидно, что длина отрезка
II. 1. Пусть теперь 2. Умножим на 3. Тогда неравенство 4. Так как угол 5. Функция Следовательно, записанное неравенство Итого: если обобщить результаты, полученные в I и II, то получим III. 1. Если 2. Таким образом, для ч.т.д. Первый замечательный предел
Доказательство 1. Рассмотрим дугу окружности радиуса
2. Проведем касательную 3. Так как 4. 5. Очевидно, что площадь треугольника 6. Или 7. Разделим все части неравенства на 8. Найдем обратные величины от каждой части неравенства:
9. Так как функция Замечание Так как функции Следствие№1. Доказательство
ч.т.д. Следствие№2. Доказательство 1. Функция 2. Обозначим 3. Функция 4. Поскольку 5. Вычислим предел 6. Итак, ч.т.д. Следствие№3. Доказывается аналогично Следствию№2. Доказать самостоятельно. Теорема о необходимом и достаточном условии существования предела функции при (Критерий Коши существования предела функции в точке) Теорема. Для того чтобы функция Доказательство необходимости 1. Пусть 2. Так как 3. Пусть также по заданному 4. Сложим неравенства п.2 и п.3: 5. Воспользуемся свойством модуля разности двух действительных величин:
Доказательство достаточности 1. Пусть 2. Возьмем произвольную последовательность значений аргумента 3. По определению предела последовательности найдется такой номер 4. Наряду с номером 5. Тогда по условию теоремы будет выполняться неравенство: 6. Это неравенство выполняется при единственном требовании, что их номера были больше 7. Неравенство 8. Так как Замечание. Если
Модуль Тема №3
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 483; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.72.224 (0.06 с.) |
 , то существуют и конечные пределы
, то существуют и конечные пределы 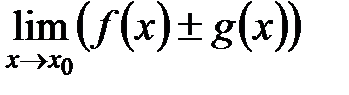 ;
; 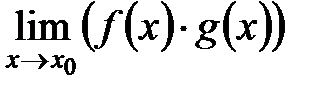 ;
;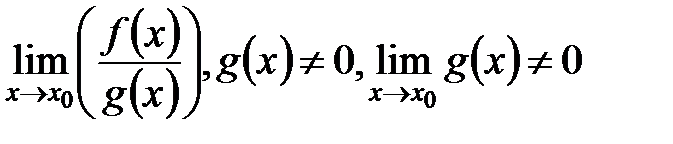 ,
,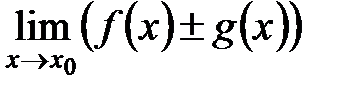 =
= 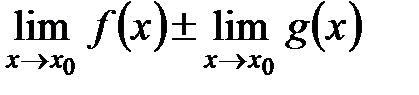 ;
;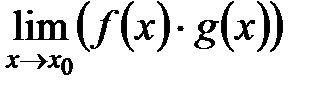 =
= 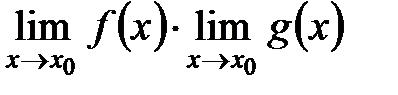 ;
; 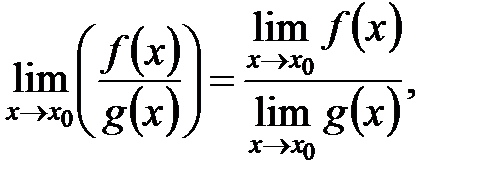
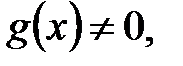
 .
.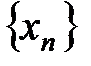 - произвольная последовательность значений аргумента для функций
- произвольная последовательность значений аргумента для функций 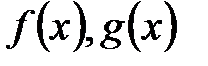 , и пусть
, и пусть 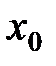 при
при  .
. и
и 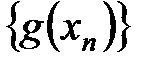 , будут иметь конечный пределы, так как по условию теоремы функции
, будут иметь конечный пределы, так как по условию теоремы функции 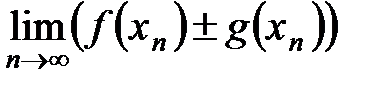 =
= 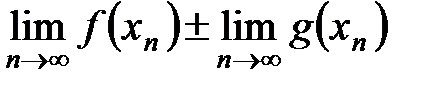 ;
; 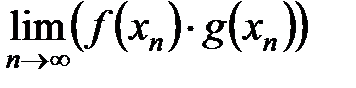 =
=  ;
;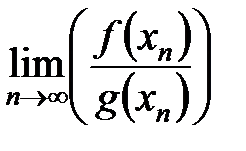
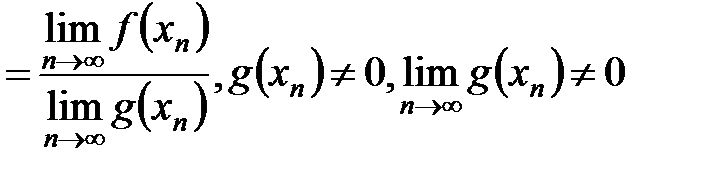 .
.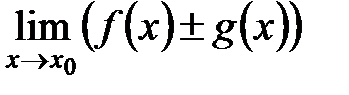 =
= 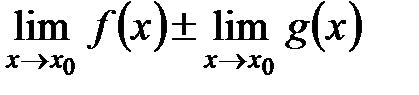 ;
; 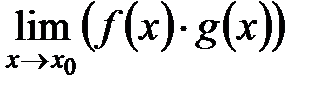 =
= 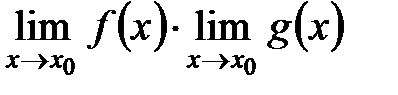 ;
;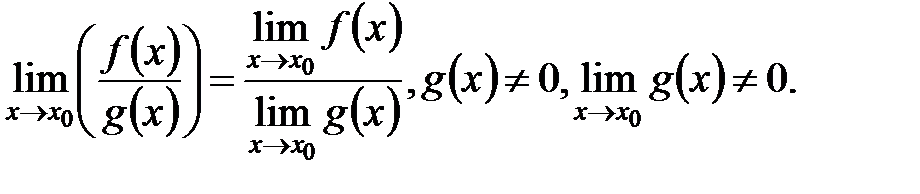
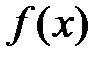 в точке
в точке 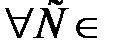 R справедливо равенство
R справедливо равенство 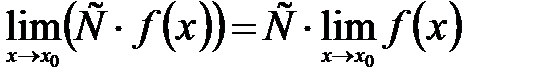 (т.е. const можно выносить за знак предела).
(т.е. const можно выносить за знак предела). (предел степени равен степени предела),
(предел степени равен степени предела), 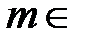 N.
N. и
и  :
:  и
и 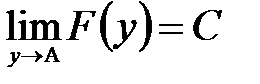 . Кроме того, пусть в некоторой проколотой
. Кроме того, пусть в некоторой проколотой 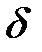 - окрестности точки
- окрестности точки 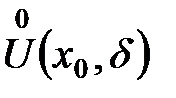 ) определена функция
) определена функция  . Тогда в точке
. Тогда в точке 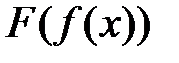 и
и  .
. и
и 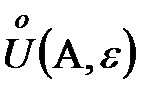 , при
, при 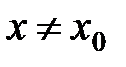 и
и 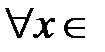
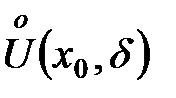 и
и 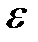 - окрестности точки
- окрестности точки 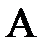 , т.е.
, т.е. 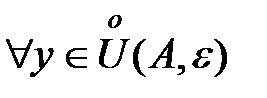 и
и 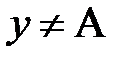 .
.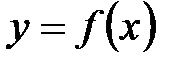 , то значения функции
, то значения функции 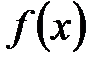 являются областью определения функции
являются областью определения функции 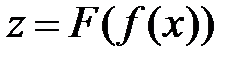 .
.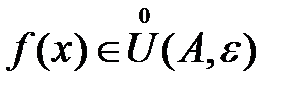 .
.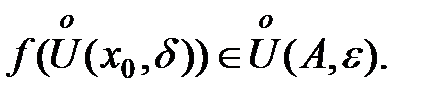
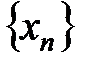 , сходящуюся к
, сходящуюся к 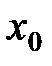 . Причем, такую последовательность
. Причем, такую последовательность 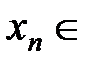
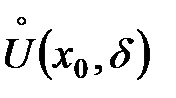 при
при 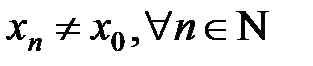 и
и  .
.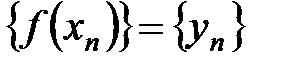 .
. , то предел последовательностей значений функции
, то предел последовательностей значений функции 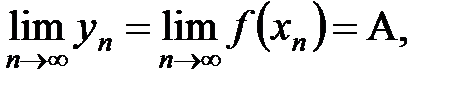
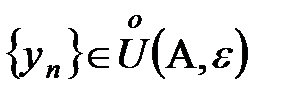 (при
(при  существует и равен
существует и равен 
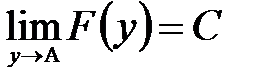 и
и  , то в соответствии с определением предела функции в точке по Гейне
, то в соответствии с определением предела функции в точке по Гейне  .
.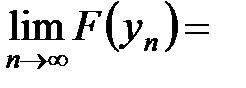
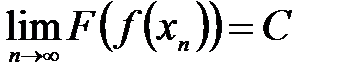 .
.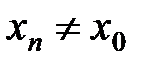 (
( соответствующая последовательность значений функции
соответствующая последовательность значений функции  , то по определению предела функции в точке по Гейне функция
, то по определению предела функции в точке по Гейне функция  при
при 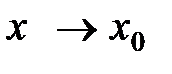 :
: 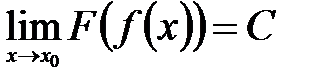 .
.
 при
при 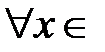 R
R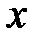 справедливо неравенство
справедливо неравенство 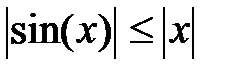 .
. с центром в точке
с центром в точке  .
. образует угол
образует угол  с радиусом
с радиусом  и угол
и угол 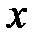 – острый, т.е.
– острый, т.е. 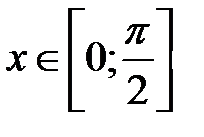 .
.
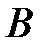 перпендикуляр
перпендикуляр 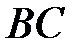 на радиус
на радиус  .
.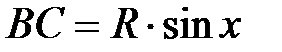 .
. симметрично радиусу
симметрично радиусу 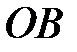 относительно радиуса
относительно радиуса  и поэтому
и поэтому 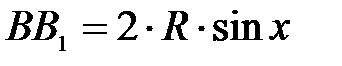 .
. 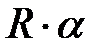 ,
, 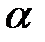 -центральный угол в радианах.
-центральный угол в радианах.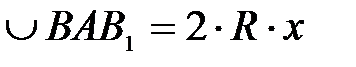 .
.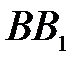 не превышает длины дуги
не превышает длины дуги  , т.е.
, т.е. 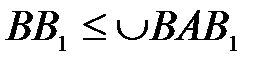 или
или 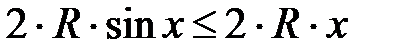 или
или 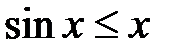 ,
, 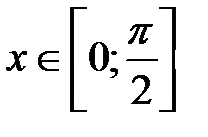 . Так как
. Так как 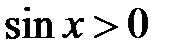 в
в 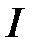 четверти, то справедливо
четверти, то справедливо 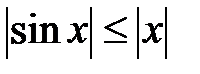 для
для  .
.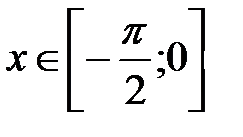 , т.е.
, т.е. 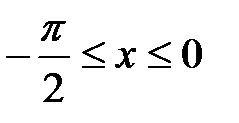 .
.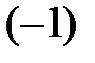 все части неравенства п.1:
все части неравенства п.1: 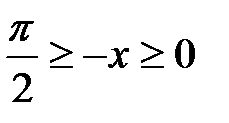 или
или 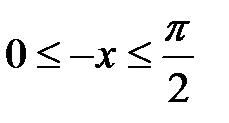 .
.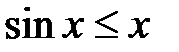 примет вид:
примет вид: 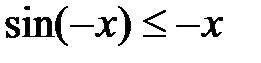 .
.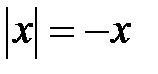 .
.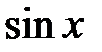 нечетная:
нечетная:  и
и 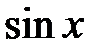 в 4-й четверти отрицательный.
в 4-й четверти отрицательный.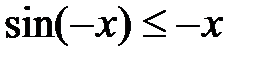 можно заменить на
можно заменить на 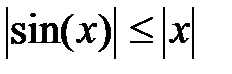 при
при  .
. при
при 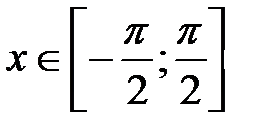 , т.е.
, т.е. 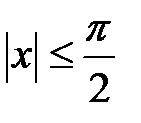 .
.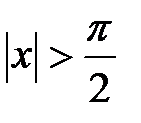

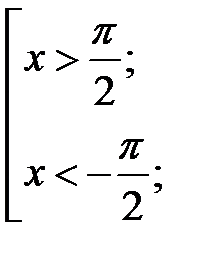 , то
, то 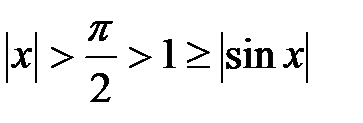 ,
, 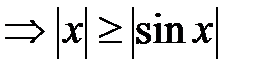 при
при 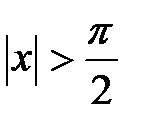 .
. R
R 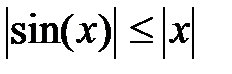 .
.
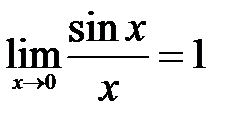
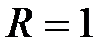 с центральным углом, радианная мера которого равна
с центральным углом, радианная мера которого равна 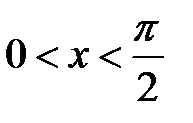 .
.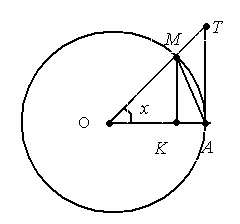

 к точке
к точке  , т.е.
, т.е. 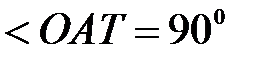 .
. то
то 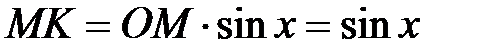 .
.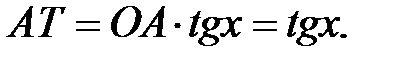
 меньше площади сектора
меньше площади сектора 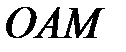 . А площадь сектора
. А площадь сектора 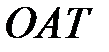 или можно записать:
или можно записать: 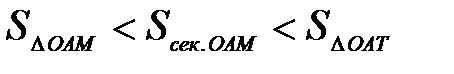 или
или 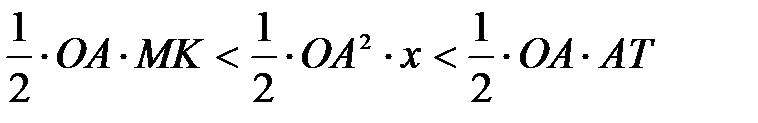 , так как известно, что площадь сектора вычисляется по формуле
, так как известно, что площадь сектора вычисляется по формуле 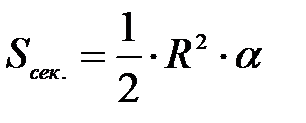 , а длина дуги
, а длина дуги 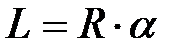 , где
, где  центральный угол.
центральный угол. или (
или (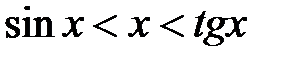 ).
). , так как
, так как 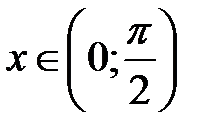 , получим
, получим 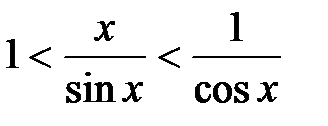 .
.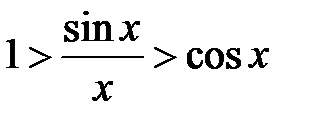 или
или 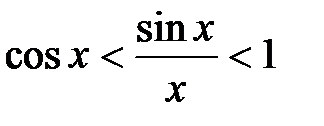 ,
, 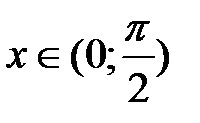 .
.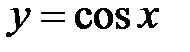 при
при 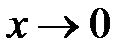 имеет предел, равный
имеет предел, равный 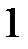 , т.е.
, т.е.  , то в соответствии с теоремой о сжатой переменной
, то в соответствии с теоремой о сжатой переменной 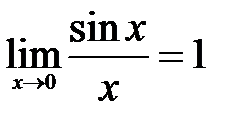 . ч.т.д.
. ч.т.д.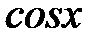 и
и 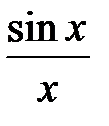 четны, то неравенство
четны, то неравенство  справедливо и при
справедливо и при 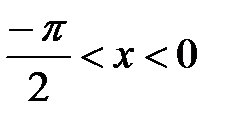 .
.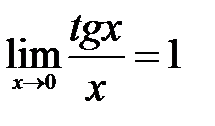
 .
.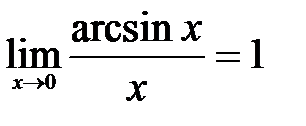
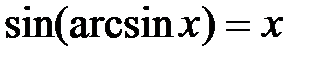 строго монотонна и непрерывна на
строго монотонна и непрерывна на 
 , тогда
, тогда 
 , обратная функции
, обратная функции 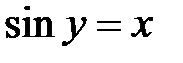 также строго монотонна и непрерывна на отрезке
также строго монотонна и непрерывна на отрезке  .
. , а
, а 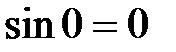 , то записи
, то записи 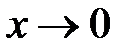 и
и 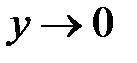 эквивалентны.
эквивалентны.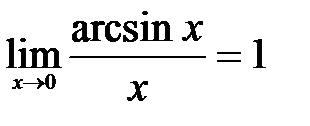 , для этого применим правило замены переменных для пределов непрерывных функций.
, для этого применим правило замены переменных для пределов непрерывных функций.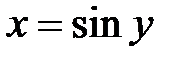 , тогда
, тогда 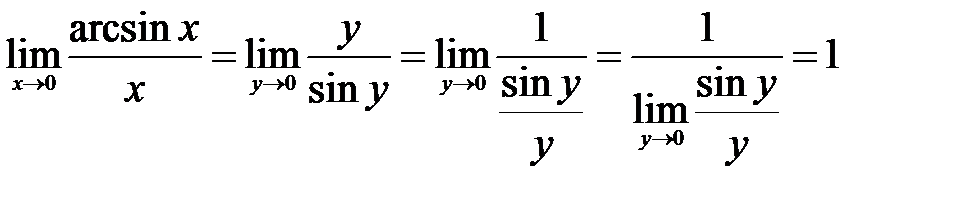 .
.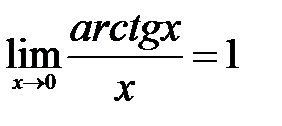 .
.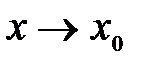
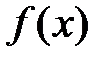 имела в точке
имела в точке 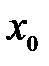 конечный предел, необходимо и достаточно, чтобы для любого
конечный предел, необходимо и достаточно, чтобы для любого 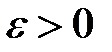 существовало такое
существовало такое 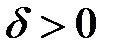 , что для всех
, что для всех 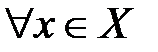 , таких, что
, таких, что 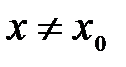 , и
, и  , таких, что
, таких, что 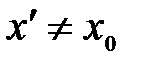 , удовлетворяющих неравенствам
, удовлетворяющих неравенствам 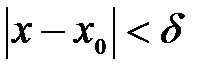 и
и 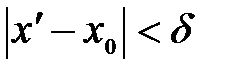 , выполнялось бы неравенство:
, выполнялось бы неравенство: 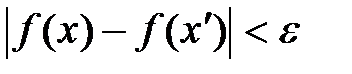 .
. , т.е.
, т.е.  . Надо доказать, что будут выполняться неравенства:
. Надо доказать, что будут выполняться неравенства: 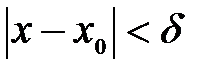 ,
, 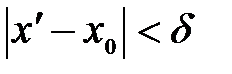 ,
, 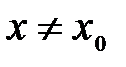 ,
, 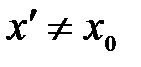 и
и 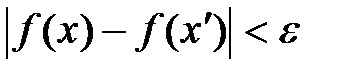 .
. , то на основании определения предела функции в точке по Коши можно записать:
, то на основании определения предела функции в точке по Коши можно записать: 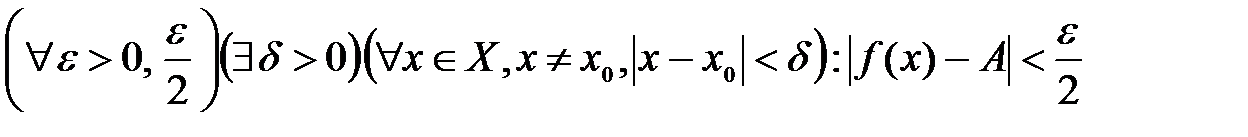 .
.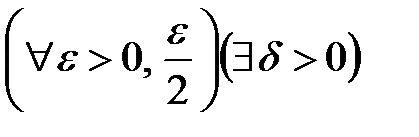 , что для
, что для  ,
,  ,
, 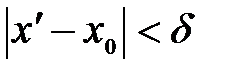 будет выполняться неравенство
будет выполняться неравенство 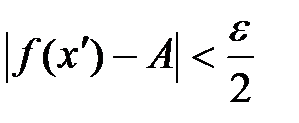 .
.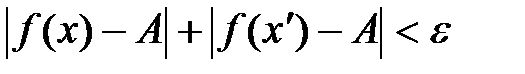 .
. .
.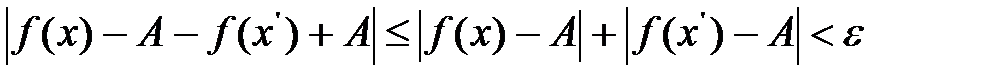 или
или 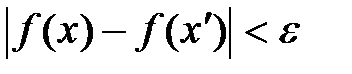 . ч.т.д.
. ч.т.д.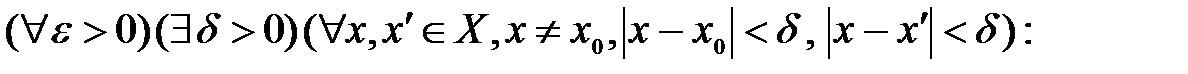
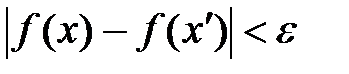 . Требуется доказать, что
. Требуется доказать, что 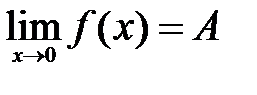 ,
,  R.
R.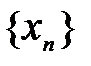 , сходящуюся к
, сходящуюся к 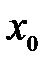 ,
, 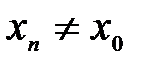 ,
, 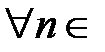 N.
N.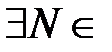 N, что при
N, что при  будет выполняться неравенство
будет выполняться неравенство 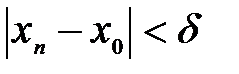 .
.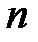 , возьмем другой номер
, возьмем другой номер 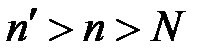 , чтобы одновременно выполнялись неравенства:
, чтобы одновременно выполнялись неравенства: 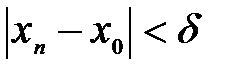 и
и 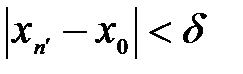 .
.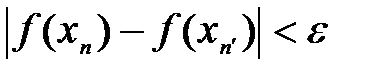 .
.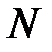 :
: 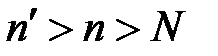 .
.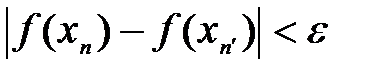 говорит о том, что последовательность значений функций
говорит о том, что последовательность значений функций 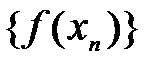 имеет конечный предел на основании критерия Коши сходимости последовательности, т.е.
имеет конечный предел на основании критерия Коши сходимости последовательности, т.е.  .
.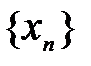 - произвольная сходящаяся к
- произвольная сходящаяся к  последовательность значений аргумента при
последовательность значений аргумента при 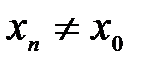 ,а
,а 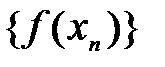 - соответствующая ей последовательность значений функции, сходящаяся к конечному числу
- соответствующая ей последовательность значений функции, сходящаяся к конечному числу 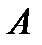 , то на основании определения предела функции
, то на основании определения предела функции 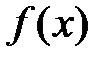 в точке
в точке 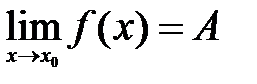 . ч.т.д.
. ч.т.д.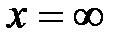 , то критерию Коши можно придать следующий вид:
, то критерию Коши можно придать следующий вид: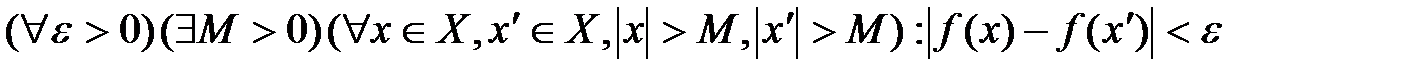 .
.


