
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ограниченность сходящейся последовательности
Определение. Последовательность {xn} называется ограниченной свер-ху, если существует число М такое, что для всех элементов последователь-ности выполняется неравенство:
Рис.5. Все элементы последовательности Пример. Определение. Последовательность {xn} называется ограниченной сни-зу, если существует число т такое, что для всех элементов последователь-ности выполняется неравенство:
Рис.6. Все элементы последовательности Пример. Определение. Последовательность
Рис.7. Все элементы последовательности Пример. Определение. Последовательность Неограниченная последовательность сверху (снизу) может быть ограни-чена снизу (сверху). Теорема. Если последовательность имеет предел, то она ограниче-на. Доказательство. 1. Пусть 2. Выберем 3. Тогда существует такое натуральное число N, что 4. Прибавим к левой и правой частям неравенства по положительному числу 5. Воспользуемся свойством модуля суммы двух действительных чи-сел 6. Тогда левая часть неравенства пункта 4 примет вид: 7. Примем за Ч.т.д. Переход к пределу в неравенствах (Теорема о предельном переходе в неравенствах) Теорема. Если элементы сходящейся последовательности Доказательство. 1.Пусть все элементы сходящейся последовательности некоторого номера, удовлетворяют неравенству 2. Предположим обратное, то есть что а < b.
3.Так как а — предел последовательности существует такой номер последовательности N, что при 4. Последнее неравенство равносильно следующему двойному неравен-ству 5.Рассмотрим правую часть неравенства 6. Полученное противоречие доказывает теорему [29]. Ч.т.д. Замечание. Случай Следствие. Если для двух последовательностей Доказательство. 1. Будем доказывать методом от противного, т.е. пусть 2. Возьмем число 3. Рассмотрим левую часть двойного неравенства: 4. Рассмотрим правую часть двойного неравенства: 5. Если за N обозначить наибольший из номеров
6. А по условию теоремы следствие к теореме [28]. Ч.т.д.
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 544; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.144.197 (0.006 с.) |
 .
.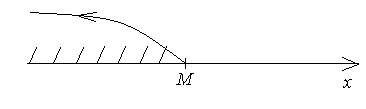
 (лежат левее точки М).
(лежат левее точки М). ограничена сверху
ограничена сверху  ,
, 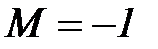 .
. .
.
 (лежат правее точки т) [28].
(лежат правее точки т) [28]. ограничена снизу
ограничена снизу  ,
,  .
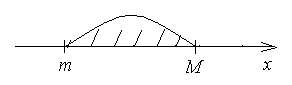
. называется ограниченной, если она ограничена и сверху, и снизу, т.е. существуют числа т и М такие, что любой элемент xn этой последовательности удовлетворяет неравенствам
называется ограниченной, если она ограничена и сверху, и снизу, т.е. существуют числа т и М такие, что любой элемент xn этой последовательности удовлетворяет неравенствам  .
.
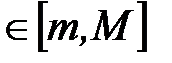 .
. ограничена, так как для любого элемента последовательности выполняется неравенство
ограничена, так как для любого элемента последовательности выполняется неравенство  ,
,  ,
,  .
. .
.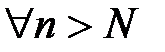 будет выполняться неравенство
будет выполняться неравенство  .
.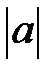 :
:  .
. .
.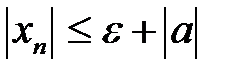 .
. , тогда
, тогда 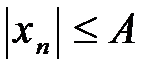 ,
, 
 - условие ограниченности последовательности. Значит последовательность
- условие ограниченности последовательности. Значит последовательность 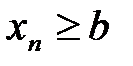 (
(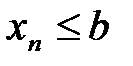 ), то и пре-дел а этой последовательности удовлетворяет неравенству
), то и пре-дел а этой последовательности удовлетворяет неравенству  (
(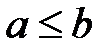 ).
). . Требуется доказать, что
. Требуется доказать, что  , где а – предел последовательности.
, где а – предел последовательности. , то для
, то для  (
( )
) n>N выполняется неравенство
n>N выполняется неравенство  или
или  .
.

 .
. . А по условию теоремы
. А по условию теоремы  доказывается аналогично.
доказывается аналогично. и
и 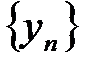 всегда вы-полняется неравенство
всегда вы-полняется неравенство  , причем каждая из них имеет конечный пре-дел,
, причем каждая из них имеет конечный пре-дел,  и
и  , то
, то  .
. при
при  между а и b в силу непрерывности действительных чисел, т.е.
между а и b в силу непрерывности действительных чисел, т.е.  .
.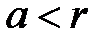 . Так как по усло-вию теоремы
. Так как по усло-вию теоремы  , то в силу теоремы о предельном переходе в неравенствах найдется такое
, то в силу теоремы о предельном переходе в неравенствах найдется такое  , что
, что 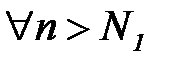 будет выполняться неравен-ство
будет выполняться неравен-ство  .
. . Так как по ус-ловию теоремы
. Так как по ус-ловию теоремы  и
и  , то в силу теоремы о предельном переходе в неравенствах найдется такое
, то в силу теоремы о предельном переходе в неравенствах найдется такое  , что
, что  будет выполняться неравен-ство
будет выполняться неравен-ство  .
. и
и  , то есть
, то есть , то для
, то для 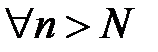 будут одновременно выполняться оба нера-венства:
будут одновременно выполняться оба нера-венства:  .
.


