
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Монополии: классификация, характеристика, особенности. Антимонопольная политика государства.
Крайней противоположностью рынка совершенной конкуренции является чистая монополия. Монополия предполагает, что одно предприятие является единственным производителем продукции, не имеющей аналогов. Покупатели при этом не имеют возможности выбора: они вынуждены приобретать продукцию предприятия-монополиста. Предположим, что структура издержек фирмы-монополиста задана кривыми АТС и МС и ТС, а предельный доход определяется кривой спроса. Каковы будут оптимальные уровни цен и объема монополиста? В условиях совершенной конкуренции текущая цена устанавливается рынком, и фирма не может воздействовать на нее, являясь ценополучателем. Для максимизации прибыли (или минимизации своих потерь, если получение прибыли невозможно) фирма должна определить оптимальный в данных рыночных и технологических условиях объем выпуска. При чистой монополии фирма может максимизировать прибыль, выбирая либо соответствующий объем, либо цену. К отраслям чистой монополии принято относить отрасли коммунального хозяйства: тепло-, водо-, газо-, электроснабжение. Практика показывает, что чистая монополия, как правило, существует в теории. Однако многие рыночные структуры по основным параметрам очень близки к ситуации чистой монополии, чем к какой-либо другой рыночной модели. Общественные издержки монопольной власти заставляют государство регулировать деятельность монополий. Антимонопольная политика — это система мер, направляемых на усиление и защиту конкуренции путем ограничения монопольной власти фирм. Среди основных направлений антимонопольной политики государства выделяют: - прямое регулирование цен; - налогообложение; - регулирование естественных монополий. Блок № 3. Теория вероятности и математическая статистика, математические методы в экономике Основные понятия алгебры множеств. Законы алгебраических множеств. Примеры. Математическим анализом называется раздел математики, занимающийся исследованием функций на основе идеи бесконечно малой функции. Основными понятиями математического анализа являются величина, множество, функция, бесконечно малая функция, предел, производная, интеграл. Величиной называется все что может быть измерено и выражено числом.
Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п. Множества обозначаются прописными буквами, а элементы множество строчными буквами. Элементы множеств заключаются в фигурные скобки. Если элемент x принадлежит множеству X, то записывают x ∈ Х (∈ — принадлежит). Если множество А является частью множества В, то записывают А ⊂ В (⊂ — содержится). Множество может быть задано одним из двух способов: перечислением и с помощью определяющего свойства. Два множества А и В равны (А=В), если они состоят из одних и тех же элементов. Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств. Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В. Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В. Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА). Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = {1,2} ∪ {5,6} = {1,2,5,6} Пример: Множество точек катета ВС и гипотенузы АС треугольника АВС являются равномощными.
Основные понятия отношений, графическое представление, свойства отношений. Часто в вычислениях необходимо выбирать элементы множеств, которые удовлетворяют некоторому " отношению ". Это понятие довольно общее, поэтому широко применимо. При соответствующем выборе отношения его аргументы могут быть связаны какой-либо формулой, иногда достаточно простой, если возможно найти удачное описание. Рассмотрим пример, иллюстрирующий понятие отношения:
Предположим, что
Если мы выберем конкретное значение из Можно рассматривать данные, приводящие к остановке, или результаты, которые не могут быть получены из Определение. Другими словами, элементы Наиболее часто встречаются отношения при Отношения не являются чем-то новым. Можно построить отношения, которые несомненно будут знакомы вам.
|
||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.142.146 (0.005 с.) |


 - множество программ;
- множество программ;  - конечное множество данных;
- конечное множество данных;  - множество результатов.
- множество результатов. , представляющие интерес. Аналогично, если мы сведем рассмотрение к
, представляющие интерес. Аналогично, если мы сведем рассмотрение к  , то
, то  связывает соответствующие данные из
связывает соответствующие данные из  .
. -местным отношением
-местным отношением  называется подмножество прямого произведения
называется подмножество прямого произведения  .
. (где
(где  ) связаны отношением
) связаны отношением  , а (
, а (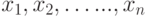 ) - упорядоченный набор из
) - упорядоченный набор из  ; в этом случае они называются бинарными отношениями. Следовательно, бинарные отношения между множествами
; в этом случае они называются бинарными отношениями. Следовательно, бинарные отношения между множествами 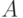 и
и  являются просто подмножеством
являются просто подмножеством  . Если эти множества эквивалентны (скажем, равны
. Если эти множества эквивалентны (скажем, равны  определяет отношения на
определяет отношения на 


