
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятность произведения событий. ⇐ ПредыдущаяСтр 2 из 2
Условной вероятностью РВ(А) события А называетсявероятность появления события А, при условии, что событие В уже произошло. События А и В независимы, если Р(А)=РВ(А) и Р(В)=РА(В). Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого Вероятность произведения двух независимых событий равна произведению их вероятностей Условная вероятность РВ(А) равна отношению вероятности совместного наступления событий А и В к вероятности события В. .– Теоремы сложения вероятностей – Теорема сложения вероятностей несовместных событий. Вероятность суммы несовместных событий равна сумме их вероятностей.
Доказательство проведём для испытания с конечным числом n равновозможных исходов. Пусть m1 – число исходов благоприятствующих событию A, а m2 – число исходов благоприятствующих событию В. Тогда вероятность события А = m1/n; а Р(В)= m2/n. Т.к. эти события несовместные, то число исходов благоприятствующих событию А + В = m1 + m2, тогда Р(А + В) = (m1 + m2)/n = m1/n + m2/n = Р(А) + Р(В). Следствие 1: Вероятность суммы нескольких попарно несовместных событий = сумме их вероятностей Р() = Р(А1) + Р(А2) +…+ Р(Аn) События А1,А2, …, Аn образуют полную группу, если они попарно несовместны и в результате испытания обязательно произойдёт хотя бы одно из них. Следствие 2: Сумма вероятностей событий, образующих полную группу, равна 1. Следствие 3. Сумма вероятностей противоположных событий равна 1. Общая теорема сложения вероятностей Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления. Р(А+В) = Р(А) + Р(В) - Р(АВ) – вероятность суммы совместных событий. Доказательство: из опр. суммы возможны три несовместных варианта: А и В произошли вместе - А۰В, произошло А, но не В – Лекция 3 Основные теоремы теории вероятности. СС-3 Формула полной вероятности. Пусть появление некоторого события А возможно лишь при наступлении одного n из попарно несовместных событий Вi, образующих полную группу и называемых гипотезами.
Тогда вероятность события А равна сумме попарных произведений вероятности каждой из этих гипотез Вi на соответствующую условную вероятность появления события А.
Формулы Байеса. Пусть появление в некотором испытании события А возможно лишь при наступлении одного n из попарно несовместных событий Вi, образующих полную группу и называемых гипотезами. Тогда, зная вероятности гипотез Р(Вi) до проведения испытания, мы можем переоценить их после проведения испытания, в результате которого появилось событие А.
где Р(Вi) – вероятности гипотез, известные до испытания (априорные вероятности гипотез),
Теорема Байеса — одна из основных теорем элементарной теории вероятностей, которая определяет вероятность наступления события в условиях, когда на основе наблюдений известна лишь некоторая частичная информация о событиях. По формуле Байеса можно более точно пересчитывать вероятность, принимая во внимание как ранее известную информацию (априорные данные), так и данные новых наблюдений (апостериорные данные). Вычисление вероятностей событий в серии независимых испытаний. Схема Бернулли - последовательность независимых испытаний (т.е. таких испытаний, вероятность исходов которых не зависит ни от номера испытания, ни от результатов предшествующих испытаний) с двумя возможными исходами. Вероятность первого исхода - А, называемого успехом, в каждом испытаний равна р, тогда вероятность второго исхода – неуспеха, равна разности единицы и р: Р(А)=р Р( Формула Бернулли Вероятность, что в серии из n испытаний по схеме Бернулли,событие А, произойдёт ровно k раз:
р – вероятность наступления события А в одном испытании,
Теорема Лапласа: применяется при больших значениях n, когда формулу Бернулли использовать сложно. Пусть Р(А)=р – вероятность проявления события А в одном испытании, тогда вероятность, что в серии из n независимых испытаний событие А произойдёт точно k раз приблизительно вычисляется по формуле Лапласа:
Интегральная теорема Лапласа. – позволяет определить вероятность того, что событие А в n независимых испытаниях произойдёт не менее
Значения функций Закон Пуассона распределения вероятностей массовых и редких событий.
где Формула Пуассона применяется, когда n – очень велико, а р – достаточно мало. Лекция 4. Случайные величины. СВ-1. Случайная величина это функция, определённая на множестве случайных событий. Случайная величина в результате эксперимента принимает те или иные числовые значения, зависящие от случайных причин. Примеры: кубик, 2 монеты, рост, вес, количество успехов и т.д.. Различают дискретные и непрерывные случайные величины. Дискретная случайная величина это случайная величина, все возможные значения которой изолированы друг от друга. Множество значений ДСВ – конечное или счётное множество. Непрерывная случайная величина – это СВ, возможные значения которой заполняют некоторый конечный или бесконечный интервал. Множество её значений имеет мощность континуума. Дискретные СВ. Закон распределения дискретной случайной величины – соответствие между всеми возможными значениями данной случайной величины и их вероятностями. Способы задания: графический, аналитический (
Значения СВ
Функция распределения случайной величины – равна вероятности, что случайная величина примет значение меньше, чем данное. График – ступенчатая возрастающая функция.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 302; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.238.76 (0.011 с.) |
 .
.
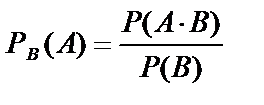
 - вероятность суммы несовместных событий
- вероятность суммы несовместных событий
 , произошло только В -
, произошло только В -  . Для независимых событий вероятность первого варианта –
. Для независимых событий вероятность первого варианта –  ; Р(
; Р( - вер. третьего. Сложив эти вероятности, получим вероятность суммы совместных независимыхсобытий
- вер. третьего. Сложив эти вероятности, получим вероятность суммы совместных независимыхсобытий
 ,
, - вероятности гипотез, вычисленные после проведения испытания, при условии, что событие А произошло (апостериорные вероятности гипотез); Р(А) – полная вероятность события А,
- вероятности гипотез, вычисленные после проведения испытания, при условии, что событие А произошло (апостериорные вероятности гипотез); Р(А) – полная вероятность события А, — вероятность наступления события А при истинности гипотезы Вi.
— вероятность наступления события А при истинности гипотезы Вi.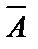 )=1-р=q.
)=1-р=q. , где
, где  число сочетаний из “n” элементов по “k” элементов в каждом.
число сочетаний из “n” элементов по “k” элементов в каждом. –вероятность не наступления события А в одном испытании, n – общее число испытаний, k – число успехов в серии из n испытаний.
–вероятность не наступления события А в одном испытании, n – общее число испытаний, k – число успехов в серии из n испытаний. , где
, где  ; где
; где  ,
,  .
. и не более
и не более  раз.
раз. , где
, где  ,
,  ;
; 
 и
и  приводятся в таблицах (см тб. 1 и 2)
приводятся в таблицах (см тб. 1 и 2) -вероятность того, что в серии из n испытаний «успех» произойдёт ровно k раз.
-вероятность того, что в серии из n испытаний «успех» произойдёт ровно k раз. , n – общее число независимых испытаний, р – вероятность «успеха» в одном испытании.
, n – общее число независимых испытаний, р – вероятность «успеха» в одном испытании. ) и табличный.
) и табличный.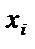



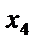







 ,
, =1. (при n
=1. (при n 
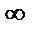 , этот ряд сходится к единице)
, этот ряд сходится к единице)
 ,
, 



