
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скорости и ускорения точек тела при сферическом движении
1. Вектор скорости. Зная вектор мгновенной угловой скорости
где
Пример 4.2. Коническое зубчатое колесо 1, насаженное с помощью шарикового подшипника на кривошип Решение. Колесо 1 совершает сферическое движение относительно точки
сферическое движение, то есть по оси собственного вращения зубчатого колеса 2 (рис. а) к примеру 4.2). Лини узлов
2. Векторы ускорения точек тела при сферическом движении. Зная вектор мгновенного углового ускорения 4.7. Теорема Ривальса: Вектор полного ускорения
где Действительно, дифференцируя по времени (4.4) по аналогии с формулой (2.22) получим формулу (4.6). Здесь
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.10.246 (0.006 с.) |
 можно определить вектор линейной скорости любой точки тела. По теореме Эйлера и формуле (2.21) для вектора скорости точки
можно определить вектор линейной скорости любой точки тела. По теореме Эйлера и формуле (2.21) для вектора скорости точки 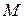 можно записать (см. рис. 4.4):
можно записать (см. рис. 4.4):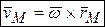 , (4.4)
, (4.4)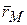 - радиус – вектор точки. Эта формула носит название формулы Эйлера. Вектор
- радиус – вектор точки. Эта формула носит название формулы Эйлера. Вектор 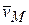 направлен по касательной к траектории точки перпендикулярно к плоскости
направлен по касательной к траектории точки перпендикулярно к плоскости 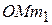 , проходящей через радиус – вектор точки
, проходящей через радиус – вектор точки 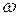 . При этом
. При этом 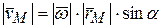 (рис.4.4). Или
(рис.4.4). Или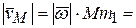
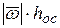 (4.5)
(4.5)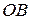 , катится по неподвижному коническому зубчатому колесу 2 (рис. а) к примеру 4.2). Угловая скорость кривошипа
, катится по неподвижному коническому зубчатому колесу 2 (рис. а) к примеру 4.2). Угловая скорость кривошипа 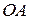 , известна и равна
, известна и равна 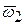 . Определить скорости точек
. Определить скорости точек  , лежащих на диаметральном сечении колеса 1, проходящем через ось кривошипа
, лежащих на диаметральном сечении колеса 1, проходящем через ось кривошипа  с некоторой угловой скоростью
с некоторой угловой скоростью  и подвижную систему координат
и подвижную систему координат 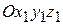 . Как и прежде подвижную ось
. Как и прежде подвижную ось 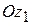 направим по оси вращения тела, совершающего
направим по оси вращения тела, совершающего
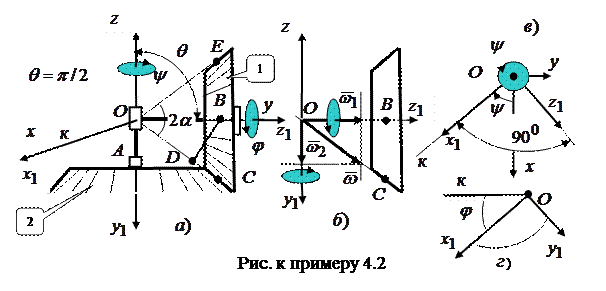
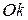 в начальный момент времени совпадает с осями
в начальный момент времени совпадает с осями 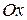 и
и 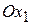 , а в процессе движения она будет над или под подвижной осью
, а в процессе движения она будет над или под подвижной осью 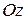 . На рис. г) к примеру 4.2 показано для произвольного момента времени положение осей координат при наблюдении с положительного конца оси
. На рис. г) к примеру 4.2 показано для произвольного момента времени положение осей координат при наблюдении с положительного конца оси 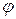 и
и 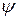 меняются. Угол
меняются. Угол 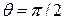 . Модули соответствующих угловых скоростей
. Модули соответствующих угловых скоростей 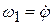 ,
, 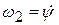 ,
,  . По (4.2) имеем
. По (4.2) имеем 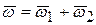 . В этом равенстве полностью известен вектор
. В этом равенстве полностью известен вектор 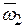 и известно направление векторов
и известно направление векторов 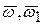 . При этом
. При этом 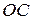 (
(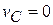 , так как это точка касания подвижного колеса с неподвижным. Рис б). Тогда из прямоугольника векторов угловых скоростей находим
, так как это точка касания подвижного колеса с неподвижным. Рис б). Тогда из прямоугольника векторов угловых скоростей находим 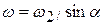 . По теореме Эйлера имеем
. По теореме Эйлера имеем 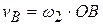 или
или 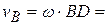
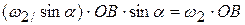 , что совпадает с предыдущим результатом. Точка
, что совпадает с предыдущим результатом. Точка 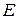 находится от мгновенной оси на расстоянии
находится от мгновенной оси на расстоянии 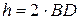 . Следовательно,
. Следовательно, 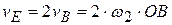 . Ответ:
. Ответ: 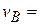
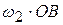 ,
, 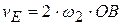 .
. можно определить линейные ускорения любой точки тела.
можно определить линейные ускорения любой точки тела.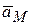 любой точки твердого тела, совершающего сферическое движение, равен сумме векторов вращательного
любой точки твердого тела, совершающего сферическое движение, равен сумме векторов вращательного 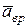 и осестремительного
и осестремительного 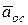 ускорений.
ускорений.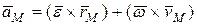 или
или 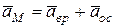 (4.6)
(4.6)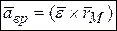 ,
, 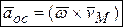 . (4.7)
. (4.7) 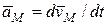 - вектор полного ускорения точки
- вектор полного ускорения точки 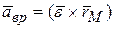 - вектор вращательного ускорения точки. Он перпендикулярен плоскости, проходящей через векторы
- вектор вращательного ускорения точки. Он перпендикулярен плоскости, проходящей через векторы 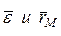 , и направлен по дуговой стрелке
, и направлен по дуговой стрелке 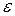 (направление определяется по правилу векторного произведения). В общем случае он не направлен по касательной к траектории, как вектор скорости точки
(направление определяется по правилу векторного произведения). В общем случае он не направлен по касательной к траектории, как вектор скорости точки 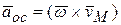 - вектор осестремительного ускорения точки тела. Этот вектор перпендикулярен плоскости, в которой лежат векторы
- вектор осестремительного ускорения точки тела. Этот вектор перпендикулярен плоскости, в которой лежат векторы 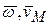 и направлен к мгновенной оси вращения
и направлен к мгновенной оси вращения  по перпендикуляру
по перпендикуляру 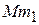 (рис.4.4).
(рис.4.4).


