
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы универсального множества
1∙а = а; 1 + а = 1; 1 + а + b + с + … + w = 1 т.е. дизъюнкция любого числа переменных обращается в единицу, если какая-нибудь одна переменная имеет значение 1, независимо от значения других переменных. 3. Законы идемпотентности (повторения, тавтологии) а∙а∙а∙ … ∙а = а а + а +... + а = а Законы двойной инверсии
т.е. двойную инверсию можно снять. 5. Законы дополнительности: а) логическое противоречие: а∙ т.е. конъюнкция любой переменной и её инверсии есть 0. в) закон исключенного третьего: а + т.е дизъюнкция любой переменной и её инверсия есть 1 6. Коммутативный закон (переместительный закон) а ∙ b = b ∙ а; a + b = b + a т.е. результат выполнения операций конъюнкции и дизъюнкции не зависит от того, в каком порядке следуют переменные. 7. Ассоциативные законы (сочетательные) a(b ∙c) = (a∙b)c = a∙b∙c; a + (b + c) = (a + b) + c = a + c + b т.е. для записи конъюнкции или дизъюнкции скобки можно упустить. 8. Дистрибутивные законы (распределительный) а) конъюнкция относительно дизъюнкции a(b + c) = ab + ac; в) дизъюнкция относительно конъюнкции a + bc = (a + b)(a + c) Законы поглощения a(a + b) = a; a(a + b)(a + c)... (a + z) = a; a + ab = a; a + ab + ac +... + az = a; a( 10. Законы склеивания (распространения) ab + a Законы обобщенного склеивания ab + (a + b)( (a + b)( 12. Законы де Моргана (законы инверсии) а) для двух переменных
т.е. инверсия конъюнкции есть дизъюнкция инверсий;
т.е. инверсия дизъюнкции есть конъюнкция инверсий; в) для n переменных
Теорема разложения F (a, b,... w) = a F (1, b,..., w) + F (a, b,... w) = [a + F(0, b,..., w)] ∙ [ Таковы основные законы алгебры логики. Справедливость любого закона алгебры логики можно доказать разными методами. Так законы 1-5 доказываются прямой подстановкой вместо переменной а значений 0 или 1, что приводит к принятым аксиомам. Справедливость приведенных законов булевой алгебры проверяется путем подстановки влогическое выражение 0 и 1, как показано в табл. 3.5 для формулы
Совпадение значений обеих частей при одинаковых наборах переменных доказывает справедливость этих законов. Булевы функции одной переменной представлены в табл. 3.6
Как видим, из четырех булевых функций практический интерес вызывает только операция отрицания F 2 = Все 16 булевых функций F0 – F15 двух переменных Х1 Х2 представлены в табл. 3.7
Как следует из табл.3.6, функции F0 и F15 — константы, F3 и F5 — повторяют, а F10 и F12 — отрицают одну из переменных, F1 и F7 — конъюнкция и дизъюнкция, которые рассмотрены ранее. К новым булевым функциям (операциям) относятся следующие. Исключение (запрет) — двухместная булева операция, результатом которой является значение единицы тогда и только тогда, когда значение одного операнда равно единице, а другого — нулю. Записывается в виде: F2 = X1 Сумма по модулю два (исключающее ИЛИ, отрицание эквивалентности) — двухместная булева операция, результатом которой является значение единицы тогда и только тогда, когда операнды имеют разные значения. Обозначается в виде: F6 = X1 Отрицание дизъюнкции (операция НЕ ИЛИ, стрелка Пирса) — булева операция, результатом которой является значение единицы тогда и только тогда, когда оба операнда равны нулю. Обозначается в виде: F8 = X1 Обобщая для п переменных, имеем: X1 Эквивалентность (равнозначность) –двухместная булева операция, результатом которой является единица тогда и только тогда, когда операнды принимают одинаковые значения. Обозначается в виде: F9 = Х1 Импликация (включение) — двухместная булева операция, результатом которой является значение нуль тогда и только тогда, когда значение одного из операндов равно нулю, а другого — единице. Обозначается в виде: F11 = X1 Отрицание конъюнкции (операция И-НЕ, штрих Шеффера, отрицание пересечения) — булева операция, результат которой равен нулю тогда и только тогда, когда оба операнда равны единице. Обозначается в виде: F14 = X1 / X2 = Обобщая для п переменных, имеем: X1 / X2 / X3... / Xn =
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 456; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.194.39 (0.029 с.) |
 = а
= а = 0
= 0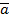 + b) = ab; a +
+ b) = ab; a + 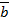 = a (a + b)(a +
= a (a + b)(a + 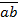 =
= 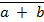 =
= 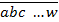 =
= 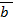 +
+  +... +
+... + 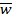 ;
; =
=  =
=  v
v 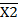 -закона де Моргана. Для доказательства построим совмещенную таблицу истинности.
-закона де Моргана. Для доказательства построим совмещенную таблицу истинности.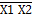 =
= 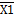 v
v  Таблица 1.9
Таблица 1.9

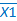
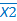


 .
. Х2
Х2
 X2
X2

 ∙X2
∙X2
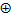 X2
X2
 Х2
Х1
Х2
Х1  Х2
Х2
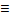 X2
X2
 X2
X2

 X2
X1
X2
X1 
 Х2
Х2
 или F4 =
или F4 =  X2.
X2. X2 =
X2 =  Х2
Х2  Х1
Х1 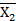
 X2 =
X2 = 
 ∙
∙ 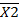 ∙
∙  ∙...
∙... 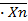 =
= 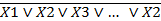
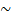 X2 = Х1 ∙ Х2
X2 = Х1 ∙ Х2 
 X2 = X1
X2 = X1  X2 =
X2 = 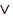 X2
X2
 =
= 



