
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация логических устройств и основные сведения о дискретных автоматахСтр 1 из 10Следующая ⇒
3.1.1 Основные определения Теоретической основой компьютерной схемотехники является алгебра логики — наука, которая использует математические методы для решения логических задач. Алгебру логики называют булевой в честь английского математика Дж. Буля, внесшего наибольший вклад в развитие этой науки. Основным предметом булевой алгебры является высказывание — простое предложение, о котором можно утверждать: истинно оно (обозначают символом 1) или ложно (обозначают символом 0). Обычно простые высказывания обозначают малыми буквами латинского алфавита, например, х1 х2,..., хn, или a, b, c, … z, которые в компьютерной схемотехнике называют переменными (аргументами). С помощью логических связок НЕ, ИЛИ, И, ЕСЛИ... ТО... строят сложные высказывания, которые называют булевыми (логическими) функциями и обозначают большими буквами латинского алфавита А, F, L, К, М, Р и др. В настоящее время главная задача алгебры логики — анализ, синтез и структурное моделирование любых дискретных конечных систем. Аппарат булевой алгебры распространяется на объекты самой различной природы безотносительно их сути, лишь бы они характеризовались двумя значениями или состояниями: контакт включен или выключен, наличие высокого или низкого уровня электрического напряжения, выполнение или невыполнение некоторого условия работы и т.д. Использование аппарата алгебры логики в компьютерной схемотехнике основано на том, что цифровые элементы характеризуются двумя состояниями, в общем случае это константы 0 и 1, и благодаря этому могут быть описаны булевыми функциями. Стандарт ДСТУ 2533-94 "Арифметические и логические операции. Термины и определения" конкретизировал основные понятия булевой алгебры в системах обработки информации. Переменную с конечным числом значений (состояний) называют переключательной, а с двумя состояниями — булевой. Функция, которая имеет, как и каждая ее переменная, конечное число значений, называется переключательной (логической). Логическая функция, число возможных значений которой и каждой ее независимой переменой равно двум, является булевой. Таким образом, булева функция — это частный случай переключательной (логической). Операция — это четко определенное действие над одним или несколькими операндами, которое создает новый объект (результат). В булевой операции операнды и результат принимают "булево значение 1 " (далее просто значение 1) и "булево значение 0 " (далее просто значение 0). Булеву операцию над одним операндом называют одноместной, над двумя — двуместной и т.д.
Булевы функции могут зависеть от одной, двух и в целом от п переменных. Запись F {X1, X2,...,Xn) означает, что некоторая булева функция F зависит от переменных Х 1, Х2,...,Х„. Основными булевыми операциями являются отрицание (операция НЕ, инверсия), дизъюнкция (операция ИЛИ, логическое сложение, объединение) и конъюнкция (операция И, логическое умножение). _ Отрицание — это одноместная булева операция F = Дизъюнкция (от анг. –разъединение)— это булева операция F = Х1 +X2 (читается "Х1 или Х2"), результатом которой является значение нуль тогда и только тогда, когда оба операнда имеют значение нуль. Часто используют запись Х v Х2 или Х1 Конъюнкция (от анг. –соединение)— это булева операция F = Х1 ∙ Х2 (читается "Х1 и Х2"), результатом которой является значение единица тогда и только тогда, когда значение каждого операнда равно единице. В выражении Х1∙ Х2 точку можно опускать, часто используют запись Х1 Операции отрицания, дизъюнкции и конъюнкции можно задать с помощью таблиц истинности (табл. 3.1, 3.2 и 3.3), в которых слева представлены значения операндов, а справа — значения булевой функции. Табл. 3.1 –Операция отрицания Табл. 3.2 –Операция дизъюнкции Табл. 3.3 –Операция конъюнкции
В таблицах булевы функции ИЛИ, И заданы для двух переменных Х1, Х2, а можно и для нескольких X1, X2, Х3 ...,Xn Областью определения булевой функции F (X1, X2,...,Хn) является конечное множество различных двоичных наборов длиной п, на каждом из которых указывается значение функции нуль или единица. Количество разнообразных двоичных наборов равно множеству n-разрядных двоичных чисел m = 2n.
Например, для функции двух переменных Х1 и Х2 имеется четыре двоичных набора: < 0,0 >; < 0,1 >; <1,0>; <1,1>. Часто наборы нумеруются десятичными эквивалентами двоичных чисел от нуля до 2n - 1. Например, для п = 4, наборы < 0101 > и < 1001 > имеют соответственно номера 5 и 9. Две функции отличаются одна от другой, если их значения будут разными, хотя бы в одном наборе. Число различных булевых функций от n переменных равно 2m, где m = 2n. Одной из интерпретаций булевых операций являются схемы, состоящие из ключей, источника напряжения Е и лампочки Л. Для реализации операции дизъюнкции двух переменных Х1 и Х2 используют два параллельно соединенных нормально разомкнутых ключа (рис. 3.4, а). При нажатии любого ключа (X1 = 1 или Х2 = 1) или обеих вместе лампочка горит (значение 1). Для реализации операции конъюнкции двух переменных X1 и Х2 применяют два последовательно соединенных нормально разомкнутых ключа (рис. 3.4, б). При нажатии одновременно обоих ключей (Х1 =Х2 = 1) лампочка горит (значение 1). Для реализации операции отрицания применяют нормально замкнутый ключ (рис. 3.4, в). При Х = О ключ замкнут, и лампочка горит; при Х= 1 ключ размыкается, и лампочка не горит.
Рисунок 3.4 – Интерпретация булевых операций: а –дизъюнкция; б – конъюнкция; в - отрицание Произвольную булеву функцию можно задать разными способами: · словесным описанием, · временными диаграммами, · геометрическими фигурами, · графами, · таблицами истинности · аналитическими выражениями. Словесное описание функций наиболее часто применяетсядля первичного, начального описания поведения логического устройства. Пример 3.1: Логическая функция трех переменных равняется единицы, если хотя бы две входные переменные равняются единицы. Пример 3.2: Словесное описание некоторой булевой функции F{X1 X2) можно представить и так: F = 1, когда Х1Х2 = 1 и F = 0, если Х1 Х2 = 0. Временная диаграмма функции представлена на рис. 3.1, а Геометрически с помощью двухмерного куба (рис.3.1,б), в котором точками выделены единичные вершины (данная функция принимает значение единицы на наборе 11). Графом, где вершины отображают значение нуля и единицы, а на ориентированных дугах переменные указывают условия переходов (рис. 3.1, в).
Рисунок 3.1 – Способы задания булевых функций Таблицы истинности. Таблица, которая содержит все возможные комбинации входных переменных Xn-1,... X2, Х1, X0 и соответствующие им значения выходных переменных Yi, называется таблицей истинности или комбинационной таблицей. В общем случае таблица истинности содержит 2n строк, где n –число переменных. Если n = 2 (22 =4) -число строк -4, для n = 3 (23 =8) -число строк -8 и т.д. Таблица 3.4 – таблица истинности логической функции 3-х переменных (для примера 3.1)
Чтобы построить таблицу, нужно вычислить значение функцииF(x1, x2, x3) для каждой из восьми комбинаций значений входных переменных. Так например, для первой строчки таблицы, при х1 =0, х2 =0, х3 =0 F(0,0,0) = 0∙0∙0 + (0+0)∙(0+1) = 0
По таблице истинности можно составить алгебраическое выражение. При этом запись алгебраического выражения осуществляется с использованием совершенной дизъюнктивной нормальной формы (СДНФ), которую рассмотрим чуть позже (гл.3.4). Аналитическое (алгебраическое) выражение или булево выражение, представляет собой формулу, состоящую из логических переменных, связанными операциями И, ИЛИ, и НЕ. Пример 3.3: F(x1, x2, x3) = х1 х2 х3 + (х1 + х2)(х1 + Как и в обычных алгебраических выражениях для задания порядка действий используются скобки. Предполагается, что выполнение операции И предшествует операции ИЛИ. Вопросы для самопроверки 1. Что такое алгебра логики и какая её главная задача. 2. Что такое высказывание и как обозначаются простые и сложные высказывания. 3. С чем связано использование аппарата алгебры логики в компьютерной схемотехнике. 4. Что такое логическая функция. 5. Что такое операция. 6. Какие булевы операции являются основными. 7. Как можно задать с помощью таблиц истинности операции И, ИЛИ, НЕ. 8. Произвольную булеву функцию можно задать разными способами, какими? 9. Приведите пример словесного описания функции. 10. Приведите пример алгебраического описания функции. Законы алгебры логики Для булевых операций отрицания, дизъюнкции и конъюнкции справедливы следующие законы, свойства и тождества: Аксиомы: определяют свойства и отношения основных операций а + в = в + а; а(в + с) = ав + ас; а + вс = (а + в)(а + с); а + а + На основе этих аксиом выводятся все теоремы, которые выражают основные законы алгебры логики. Законы нулевого множества 0 ∙а = 0; 0 + а = а; 0∙a∙b∙c ∙… ∙w = 0 т.е. конъюнкция любого числа переменных обращается в ноль, если какая-нибудь одна переменная имеет значение 0, независимо от значения других переменных.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.181.231 (0.019 с.) |
 (читается "не X'), результатом которой является значение, противоположное значению операнда.
(читается "не X'), результатом которой является значение, противоположное значению операнда. Х2
Х2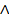 Х2, Х1
Х2, Х1  Х2 или Х1 & Х2.
Х2 или Х1 & Х2.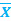


 3)
3) = 1;
= 1; ; а
; а 


