
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика розв’язання задач для змінних сил шляхом інтегрування
1. Визначаємо усі сили, що діють на точку. 2. Записуємо диференціальне рівняння руху точки під дією сили
3. Вибираємо систему координат, зручну для умов задачі, та записуємо диференціальні рівняння в проекціях на вісі. 4. Інтегруємо диференціальні рівняння та визначаємо сталі інтегрування з початкових умов. В залежності від виду сили, що діє на матеріальну точку, можливі наступні випадки: а) сила залежить лише від часу б) сила залежить лише від швидкості точки
Це рівняння допускає розділення змінних і розв’язання задачі зводиться до двох послідовних інтегрувань. Зауважимо, що після першого інтегрування знайдемо в) сила залежить лише від координати точки
і безпосередньо розділити змінні в такому рівнянні не вдається, тому виконуємо наступне перетворення
Після цього змінні в (3.1) можна розділити
і після інтегрування останнього виразу отримати
в якому Початкові умови
Після розділення змінних в (3.5) та інтегрування, отримаємо
Зауважимо, що в загальному випадку виникає складний інтеграл, який значно спрощується, коли Користуючись початковими умовами з (3.6) визначаємо другу сталу інтегрування
Приклад 1. Визначення закону руху точки, коли на неї діє сила, що залежить лише від часу. Знайти закон руху точки масою Розв’язання. Оскільки ми маємо справу з рухом в площині
Будемо окремо розв’язувати задачу для кожної координати. Для руху вздовж осі
з початковими умовами: Щоб розділити змінні, помножимо обидві частини диференціального рівняння на
Підставляючи початкові умови, маємо 2 = 6·02+ С 1, звідки знаходимо
Помножимо на
З початкових умов маємо –2 = 2·0 + 2·03 + С 2, звідки знаходимо
Для руху вздовж осі
з початковими умовами: Виконуючи ті ж самі кроки, що і для розв’язання диференціального рівняння руху вздовж осі
Підстановка початкової умови
і визначити Таким чином, вираз для швидкості приймає вигляд
Останній вираз помножимо на
Підставимо в останній вираз початкову умову
і знаходимо
Відповідь:
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 148; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.242.238 (0.012 с.) |

 .
.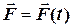 . В цьому випадку можна розділити змінні і послідовно знайти
. В цьому випадку можна розділити змінні і послідовно знайти 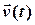 та
та 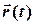 . Розв’язання задачі зводиться до інтегрування функції
. Розв’язання задачі зводиться до інтегрування функції 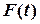 та її первісної.
та її первісної.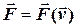 . У випадку, коли кожна декартова проекція сили залежить тільки від відповідної проекції швидкості, диференціальне рівняння руху розкладається на три скалярних рівняння. Наприклад, для x - компоненти отримуємо
. У випадку, коли кожна декартова проекція сили залежить тільки від відповідної проекції швидкості, диференціальне рівняння руху розкладається на три скалярних рівняння. Наприклад, для x - компоненти отримуємо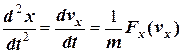 .
.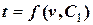 . Розв’язавши останнє рівняння відносно
. Розв’язавши останнє рівняння відносно 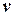 будемо мати
будемо мати 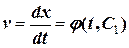 звідки повторне інтегрування дає
звідки повторне інтегрування дає 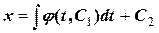 .
.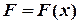 . В цьому випадку диференціальне рівняння руху точки має вигляд
. В цьому випадку диференціальне рівняння руху точки має вигляд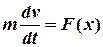 , (3.1)
, (3.1)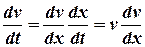 . (3.2)
. (3.2)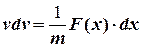 , (3.3)
, (3.3)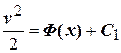 , (3.4)
, (3.4)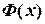 - первісна функції
- первісна функції 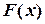 .
. =
= 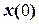 та
та  =
= 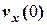 дозволяють визначити сталу інтегрування
дозволяють визначити сталу інтегрування  та явно записати
та явно записати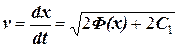 . (3.5)
. (3.5)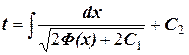 . (3.6)
. (3.6)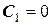 .
.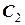 . Підставляючи її значення в (3.6) і розв’язуючи отримане рівняння відносно координати
. Підставляючи її значення в (3.6) і розв’язуючи отримане рівняння відносно координати  , знаходимо її залежність від часу та сталих інтегрування (чи початкових умов)
, знаходимо її залежність від часу та сталих інтегрування (чи початкових умов)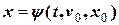 .
. = 3 кг, на яке діє сила
= 3 кг, на яке діє сила 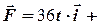
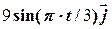 Н. На момент часу
Н. На момент часу 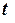 = 0 с,
= 0 с, 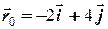 м та
м та  м/с.
м/с.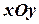 , то рівняння руху точки має вигляд:
, то рівняння руху точки має вигляд: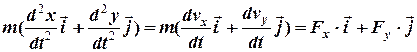 .
.
 та після інтегрування отримаємо
та після інтегрування отримаємо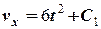 .
.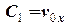 = 2 м/с, тому, останній вираз запишемо в вигляді
= 2 м/с, тому, останній вираз запишемо в вигляді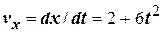 м/с.
м/с.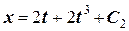 .
. = – 2 м, тому остаточне рівняння руху матеріальної точки вздовж осі
= – 2 м, тому остаточне рівняння руху матеріальної точки вздовж осі 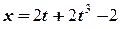 .
. , з врахуванням значення маси, отримуємо
, з врахуванням значення маси, отримуємо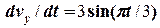 .
. 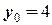 м,
м, 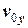 = 5 м/с.
= 5 м/с.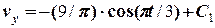 .
.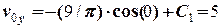 м/с,
м/с,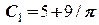 .
.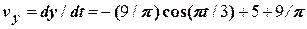 .
.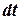 , повторно інтегруємо та отримаємо
, повторно інтегруємо та отримаємо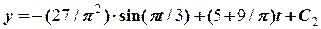 .
. ,
,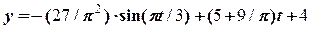 м.
м.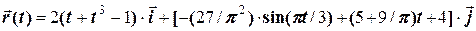 м.
м.


