
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неоднородные линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами
Дано:
характеристическое уравнение будет:
При известном общем решении однородного дифференциального уравнения частное решение неоднородного находится вариацией постоянных, а затем составляется общее решение (8). Метод вариацмм применим к (8) при Общее правило. Если
где
Здесь Если же Для обоснования рассмотрим два частных случая Случай 1.
Этот случай соответствует
где 1) многочлен 2) многочлен 3) многочлен В первом случае
из которого можно найти неопределеные коэффициенты Во втором случае,
В третьем случае
Правило 1. Если
где Пример.
Случай 2.
Сделаем замену
Таким образом, уравнение (*) сведено к частному случаю, рассмотренному выше. Следовательно:
1. Если 2.
3. Правило 2. Если
где Пример.
Перейдем теперь к общему случаю:
Вспомогательная теорема. Пусть в уравнении
Положим
отсюда, по равенству комплексных чисел, следует доказательство теоремы. Следствие. Если
Заменим теперь в общем уравнении
перегруппируем и введем новые обозначения:
тогда
|
|||||
|
Последнее изменение этой страницы: 2017-01-19; просмотров: 159; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.30.162 (0.017 с.) |
 , (8)
, (8) и
и 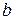 – действительные числа, соответствующее однородное уравнение имеет вид:
– действительные числа, соответствующее однородное уравнение имеет вид: ,
, .
. и в этом смысле универсален. Однако, для частных случаев
и в этом смысле универсален. Однако, для частных случаев 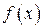 чаще применяется метод подбора.
чаще применяется метод подбора.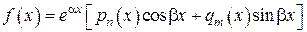 , (9)
, (9)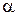 ,
,  – действительные числа,
– действительные числа,  и
и 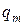 – целые рациональные функции степеней
– целые рациональные функции степеней 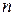 и
и  , тогда (8) имеет частное решение вида
, тогда (8) имеет частное решение вида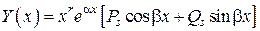 . (10)
. (10) – кратность корня
– кратность корня 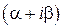 характеристического уравнения. Если же
характеристического уравнения. Если же  .
.  ,
,  и
и 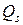 – многочлены степени
– многочлены степени  . Коэффициенты
. Коэффициенты  в (8). Далее, как обычно, общее решение есть сумма
в (8). Далее, как обычно, общее решение есть сумма  .
. для каждого случая.
для каждого случая. ,
, 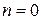 ,
, 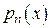 –
– 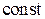 .
.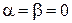 .
.  . Подставим
. Подставим  в (8), получим
в (8), получим ,
,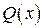 есть:
есть: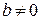 .
. -й степени, если
-й степени, если  ,
, 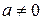 .
. -й степени, если
-й степени, если 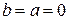 .
.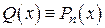 , (*)
, (*) есть корень характеристического уравнения, тождество (*) невозможно, так как степень
есть корень характеристического уравнения, тождество (*) невозможно, так как степень  . При этом степень
. При этом степень  .
. , то есть
, то есть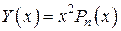 .
. ,
, – многочлен
– многочлен 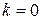 . Для вычисления неопределенных коэффициентов
. Для вычисления неопределенных коэффициентов  ,
,  , корень
, корень  ,
,

 ,
,  ,
,  и
и .
.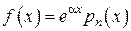 ,
, 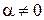 ,
, . (*)
. (*)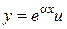
 ,
, 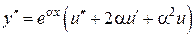
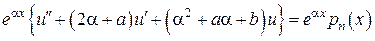
 , где
, где ,
,  .
. , тогда
, тогда 
 , где коэффициенты
, где коэффициенты  ,
,  , то есть если
, то есть если 
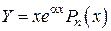 .
.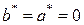 , то есть
, то есть 
 .
. ,
, ,
,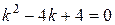

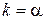 и
и  .
.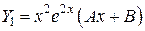 , подставляя в дифференциальное уравнение, получим:
, подставляя в дифференциальное уравнение, получим: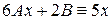
 ,
,  ,
, 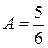 .
. .
. .
. есть решение уравнения
есть решение уравнения  ,
,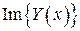 есть решение уравнения
есть решение уравнения 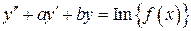 .
.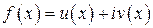 ,
, 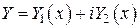 . Дважды дифференцируя
. Дважды дифференцируя 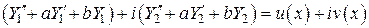 ,
, есть решение уравнения
есть решение уравнения  , то
, то  есть решение уравнения
есть решение уравнения  .
. и
и 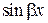 по формулам Эйлера:
по формулам Эйлера: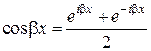 ,
,  ,
, ,
, 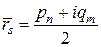 ,
,  .
.


