
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дисперсия и среднее квадратическое отклонение случайной величины. Свойства дисперсии. Производящая функция.
В теории вероятностей Дисперсия случайной величины Х называется математическое ожидание Е (Х — mх)2 квадрата отклонения Х от её математического ожидания mх = Е (Х). Д. случайной величины Х обозначается через D (X) или через s2X. Для случайной величины Х с непрерывным распределением вероятностей, характеризуемым плотностью вероятности р (х), дисперсия вычисляется по формуле где Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата ее отклонения от ее математического ожидания:
Замечание 1. В определении дисперсии оценивается не само отклонение от среднего, а его квадрат. Это сделано для того, чтобы отклонения разных знаков не компенсировали друг друга. Замечание 2. Из определения дисперсии следует, что эта величина принимает только неотрицательные значения. Замечание 3. Существует более удобная для расчетов формула для вычисления дисперсии, справедливость которой доказывается в следующей теореме: D (X) = M (X ²) – M ²(X). (7.7) Доказательство. Используя то, что М (Х) – постоянная величина, и свойства математического ожидания, преобразуем формулу (7.6) к виду: D (X) = M (X – M (X))² = M (X ² - 2 X·M (X) + M ²(X)) = M (X ²) – 2 M (X)· M (X) + M ²(X) = = M (X ²) – 2 M ²(X) + M ²(X) = M (X ²) – M ²(X), что и требовалось доказать.
Свойства дисперсии.
1) Дисперсия постоянной величины С равна нулю: D (C) = 0. (7.8) Доказательство. D (C) = M ((C – M (C))²) = M ((C – C)²) = M (0) = 0. 2) Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат: D (CX) = C ² D (X). (7.9) Доказательство. D (CX) = M ((CX – M (CX))²) = M ((CX – CM (X))²) = M (C ²(X – M (X))²) = = C ² D (X). 3) Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D (X + Y) = D (X) + D (Y). (7.10) Доказательство. D (X + Y) = M (X ² + 2 XY + Y ²) – (M (X) + M (Y))² = M (X ²) + 2 M (X) M (Y) + + M (Y ²) – M ²(X) – 2 M (X) M (Y) – M ²(Y) = (M (X ²) – M ²(X)) + (M (Y ²) – M ²(Y)) = D (X) + D (Y). Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме их дисперсий. Следствие 2. Дисперсия суммы постоянной и случайной величин равна дисперсии случайной величины. 4) Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: D (X – Y) = D (X) + D (Y). (7.11) Доказательство. D (X – Y) = D (X) + D (- Y) = D (X) + (-1)² D (Y) = D (X) + D (X).
Дисперсия дает среднее значение квадрата отклонения случайной величины от среднего; для оценки самого отклонения служит величина, называемая средним квадратическим отклонением. Средним квадратическим отклонением σ случайной величины Х называется квадратный корень из дисперсии:
Опр:Средним квадратическим отклонением Замечание:матем.ожидание М(х) характеризует среднее значение С.В. Дисперсия D(x)характеризует квадратичное отклонение С.В. от среднего значения: Св-ва D(x): 1)D(c)=0: 2)D(k*x)= Док-во:D(k*x)=M M 3)дисперсия D(x+-y)=D(x)+D(Y) 4)D(x)=M(x2)-(M(x))2 Док-во:D(x)=M(x-M(x))2)=M(x2-2x*M(x)+M2(x))=M(x2)-2M(x)*M(M(x))+M(M2(x))=M(x2)-2M(x)*M(x)+M2(x)=M(x2)-M2(x) M(x) M2(X)-постоянные величины
Производящей функцией случайной величины x называется функция комплексного переменного z
производящая функция последовательности f 0, f 1..., fn... функция
(в предположении, что этот степенной ряд сходится хотя бы для одного значения t ¹ 0). Производящая функция называют также генератрисой. Последовательность f 0, f 1..., fn... может быть как числовая, так и функциональная; в последнем случае Производящая функция зависит не только от t, но и от аргументов функций fn. Например, если fn = aqn где а и q - постоянные, то Производящая функция
если fn - Фибоначчи числа; f 0 = 0, f 1 = 1, f n+2= f n+1+ f n, то Производящая функция
если f n = Т n(х) - Чебышева многочлены: T 0(х)= 1, T n (х)= cos (n arc cos x), то Производящая функция
и т.д. Знание Производящая функция последовательности часто облегчает изучение свойств последней. Производящая функция применяются в теории вероятностей, в теории функций и в алгебре (в теории инвариантов). Впервые метод Производящая функция был применен П. Лапласом для решения некоторых проблем теории вероятностей.
|
|||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 841; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.169.94 (0.01 с.) |


 . (7.12)
. (7.12) (х) С.В.Х. называется число
(х) С.В.Х. называется число 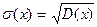
 *D(x)
*D(x) =
=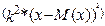 =
= 

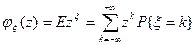 , |z|£1.
, |z|£1.






