
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порядок перевода «сырых» показателей психодиагностических методик в стандартные единицы измерения (стены)Содержание книги
Поиск на нашем сайте
Исследование психических явлений требует многоаспектного анализа и применения разнообразного набора его конкретных методов в соответствии с поставленными задачами и общей стратегией проведения комплексной психодиагностики. При проведении мероприятий по профессиональному психологическому отбору и профессионально-психологическому сопровождению обучающийся обследуется с помощью целого комплекса методик, которые могут иметь совершенно различный интервал тестовых показателей. Полученные при сборе данных «сырые» (первичные) оценки далеко не всегда удобно использовать в дальнейшей работе. Особенно, когда возникает необходимость сравнить показатели испытуемого по разным методикам, получить интегральный показатель развития изучаемых качеств или отнести их к какой либо группе («успешных», «не успешных», «норме»). Для этого «сырые» оценки тем или иным способом преобразуют в значения стандартных тестовых шкал. Данные преобразования позволяют оценивать индивидуальный результат тестирования путем сопоставления его с тестовыми нормами (стандартной тестовой шкалой), полученными на выборке стандартизации. Выборка стандартизации специально формируется для разработки стандартной шкалы – она должна быть репрезентативна генеральной совокупности, для которой планируется применять данный тест, методику. Для получения нормального распределения величины измеряемого тестом свойства требуемое число испытуемых в ней обычно составляет не менее 200 человек. Впоследствии при тестировании предполагается, что и испытуемый, и выборка стандартизации принадлежат одной и той же генеральной совокупности. При стандартизации результатов тестовых испытаний чаще всего используется показатель среднеквадратичного отклонения – s. Стандартизация осуществляется при условии нормального распределения тестовых оценок в репрезентативной выборке испытуемых или близком к нему (рис. 1). Нормальным такое распределение называется потому, что оно очень часто встречалось в естественнонаучных исследованиях и казалось «нормой» всякого массового случайного проявления признаков. Это распределение следует закону, открытому тремя учеными в разное время: Муавром в 1733 г. в Англии, Гауссом в 1809 г. в Германии и Лапласом в 1812 г. во Франции. График нормального распределения может быть получен из полигона эмпирического распределения при бесконечном увеличении числа наблюдений и сужении интервалов до размеров точки. Он представляет собой куполообразную кривую, симметричную относительно центра группирования, имеющую строго определенные пропорции.
Рисунок 1 – Нормальное распределение тестовых оценок в репрезентативной выборке испытуемых
Параметры распределения – это его числовые характеристики, указывающие, где «в среднем» располагаются значения признака, насколько эти значения изменчивы и наблюдается ли преимущественное появление определенных значений признака. В реальных психофизиологических исследованиях оперируют не параметрами, а их приближенными значениями, так называемыми оценками параметров. Числовые характеристики выборки дают количественное представление об эмпирических данных и позволяют сравнивать их между собой. Наибольшее практическое значение имеют: - характеристики положения исследуемой совокупности (среднее арифметическое значение признака, медиана, мода); - характеристики рассеяния (дисперсия); - характеристики асимметрии (показатели асимметрии и эксцесса). Среднее арифметическое (оценка математического ожидания) вычисляется по формуле:
(1) Символ S обозначает сумму всех значений xi, когда i принимает значения от 1 до n; xi – общий член последовательности, подлежащий суммированию; i – индекс суммирования, порядковый номер члена последовательности; n – количество наблюдений. Медианой (Ме) называется такое значение признака, когда одна половина значений экспериментальных данных меньше ее, а вторая больше. Мода (Мо) представляет собой значение признака, встречающееся в выборке наиболее часто. При нормальном распределении признака значения среднего арифметического, медианы и моды близки или совпадают друг с другом Среднее квадратическое отклонение (s) - мера рассеяния вариант или оценка дисперсии - определяется по формуле:
(2) где: xi – каждое наблюдаемое значение признака; `x - среднее арифметическое значение признака; n – количество наблюдений. При нормальном распределении наибольшее отклонение крайней варианты от среднего арифметического составляет примерно 3s (правило «трех сигм»). Имеется определенное статистическое соответствие между отклонением признака от среднего арифметического и положением его в упорядоченном вариационном ряду. Кривая нормального распределения с процентным выражением распределений относительных частот в зависимости от величины отклонения от среднего арифметического представлена на рисунке Одним из способов преобразования «сырых» результатов тестирования является нормирование. Суть нормирования состоит в переходе к другому масштабу — стандартным единицам измерения. Значимость стандартных шкал заключается, прежде всего, в том, что они позволяют отражать в одинаковых единицах измерения разнородные параметры, которые в обычных для этих параметров единицах измерения несопоставимы. Простейшей из стандартных шкал является Z-шкала. Первичные значения показателя могут быть преобразованы в Z-оценки по формуле:
где: `x – среднее арифметическое показателя в выборке стандартизации; xi – величина показателя теста в выборке стандартизации; s – среднее квадратическое отклонение величин признака в выборке стандартизации.
Положительные значения Z-оценки соответствуют величинам выше среднего уровня, отрицательные значения - величинам ниже среднего. Единицей этой шкалы измерения является величина среднего квадратического отклонения. Среднее значение шкалы Z-оценок равно нулю. Использование Z-оценок не всегда удобно, т.к. они могут принимать отрицательные и дробные значения. Поэтому часто Z-оценки преобразуют в другие шкалы, имеющие заданные среднее квадратическое отклонение и среднее значение. При этом используется формула:
где: `xз – заданное среднее значение шкалы; sз – заданное среднее квадратическое отклонение. Например, Р.Б. Кеттелл для стандартизации показателей методики 16-ФЛО предложил шкалу стенов – «стандартной десятки», где: 5,5 – заданное среднее значение показателя; 2 – заданное среднее квадратическое отклонение. Стенирование является одним из способов приведения нормированных оценок к виду, удобному для практического использования. Оно представляет собой перевод исходных тестовых оценок в выборке стандартизации в 10-балльную равноинтервальную шкалу (шкалу стенов). Практически это достигается путем разбиения оси значений тестовых оценок в выборке стандартизации на 10 интервалов, соответствующих долям среднеквадратичного отклонения s. При этом M (средняя арифметическая величина признака в выборке стандартизации) принимается за среднюю точку шкалы стенов. При этом всякое значение тестовых оценок, входящее в интервал от M до M + 0,5s, приравнивается к 6 баллам по шкале стенов, а, входящее в интервал от M до M – 0,5s, – к 5 баллам этой шкалы. Такая же процедура с шагом увеличения равным 0,5s проводится для вычисления 7, 8, 9 и 10 баллов стеновой шкалы и с шагом уменьшения на 0,5 s – для вычисления 4, 3, 2, и 1 балла шкалы стенов (рис.1).
Получение 10 балльного ряда и есть шкала перевода «сырых» оценок в стены. При такой системе стандартизации диапазон, который принято называть средним или нормой (диапазон в 1s), характеризуется стандартными единицами от 4 до 7 стенов. Стандартные оценки от 3 или 8 стенов свидетельствуют об индивидуальных различиях, выходящих за границы средней нормы. Оценки в 2 и 9 стенов получаются при значительном отклонении индивидуальных оценок, на 2s выше и ниже среднего группового значения. Максимальная оценка в 10 стенов достигается при отклонении индивидуального тестового результата на 2,5s и более, вверх от средней нормы. Аналогичным образом, оценка в 1 стен ставится за все отклонения индивидуального тестового результата от среднего значения на 2,5s и ниже. Для перевода «сырых» оценок в стены можно также использовать формулу линейного преобразования шкалы Z – оценок (
St = 2 × (
где Xi – значение признака (в «сырых» баллах); M – среднее арифметическое значение признака; σ – среднеквадратичное отклонение значений признака. При отклонении распределения значений признака (оценок в «сырых» баллах) от их нормального распределения используют процентильную шкалу перевода оценок в стены. Процентиль (X%) – это такое значение «сырой» оценки, которое соответствует частоте оценок меньших и равных по значению данной «сырой» оценке в %. Перевод значения «сырой» оценки, выраженной в процентилях, в стены осуществляется по стандартной шкале (рисунок 1, таблица 2), где значения оценок в стенах связаны с величинами частот. Для каждого теста по результатам тестирования стандартизованной выборки с использованием шкалы перевода процентилей в стены определяют границы стеновых оценок в значениях «сырых» оценок и строят шкалу перевода «сырых» оценок теста в стены (рисунок 1, таблица 2),. Границы стеновых оценок в значениях «сырых» оценок определяют по граничным значениям частотных интервалов, указанных в таблице 1 для каждой стеновой оценки. Например, по результатам обследования результат испытуемого входит в диапазон «сырых» оценок (X5) стандартизованной выборки, что соответствует частоте оценок в % (процентиль) [30,86; 50,0] и, соответственно, 5 стенам.
Таблица 1. Перевод процентильной шкалы в стены
При создании стеновой шкалы следует учитывать конструктивные особенности теста. Возможно создание стеновой шкалы на основе обратно пропорциональной зависимости, когда более высокий «сырой» балл свидетельствует о меньшей степени выраженности изучаемой характеристики, например, такая шкала применяется в тесте «Адаптивность».
Приложение 27
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 7785; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

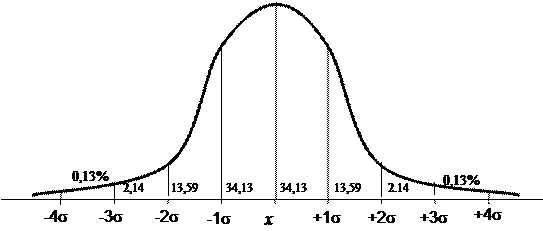
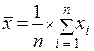
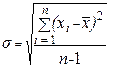
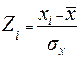 :
: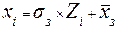
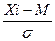 ) нормального распределения в десятибальную шкалу стенов:
) нормального распределения в десятибальную шкалу стенов: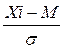 )+ 5,5,
)+ 5,5,


