
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение зависимости числовых характеристик от пробега
Согласно представлениям теории изнашивания обычно считается, что кривая износа имеет вид, представленный на рис. 6.
Рис. 6. Зависимость величины износа узлов электроподвижного состава от пробега: 1 – приработочный период; 2 – период нормальной эксплуатации; 3 – период усиленного износа.
В табл. 9 в качестве примера приведены числовые характеристики распределения величины проката бандажей колесных пар при различных значениях пробега L. Эта таблица задает эмпирические зависимости M*y (L) и s *y (L), которые на рис. 6 и 7 показаны пунктирными линиями.
Таблица 9 – Числовые характеристики распределения величины проката бандажей колесных пар электровозов
На практике значения контролируемых параметров изнашиваемых деталей локомотивов замеряют не чаще, чем при ТР-1. Однако период приработки после восстановления бандажей на ремонте ТР-3, СР или КР заканчивается уже к первому ТР-1. Кроме того, допуски на значения контролируемых параметров М доп. устанавливаются с таким расчетом, чтобы предупредить наступление периода усиленного изнашивания (см. рис. 6). Поэтому значения контролируемых параметров представляют только второй участок функции – период нормальной эксплуатации, где зависимость контролируемых параметров от пробега близка к линейной. Об этом свидетельствует анализ полей корреляции числовых характеристик контролируемых параметров, представленных на рис. 7 и 8.
Рис. 7. Зависимость среднего значения контролируемого параметра от пробега
Рис. 8. Зависимость среднеквадратического отклонения контролируемого параметра от пробега
Для аппроксимации эмпирических зависимостей аналитическими функциями надо выбрать свой вид зависимости. В общем плане аналитическую зависимость можно представить в виде некоторой нелинейной функции y = f (a 1, a 2, …, a S, li) одного аргумента li, в выражение которой входит S параметров a 1, a 2, …, a S, li. С помощью этой функции необходимо аппроксимировать эмпирическую регрессию, которая задана в виде N точек (li, yi) при i = 1, 2,…, N, где под y следует понимать один из параметров рассматриваемого закона распределения. Параметры функции y находятся методом наименьших квадратов, согласно которому сглаживающая линия проводится таким образом, чтобы сумма квадратов отклонений экспериментальных точек от нее обращалась в минимум. При этом вероятность того, что выбранная теоретическая линия действительно отражает полученную в эксперименте закономерность, оказывается максимальной, т. е. эта линия является наиболее вероятной.
Условие метода наименьших квадратов записывается в виде: Z (a 1, a 2, …, a S) = или
где f (Li) – выбранная аппроксимирующая функция; Yi и Li – полученная совокупность экспериментальных данных. Здесь
Зависимости My (L) и s y (L) ищем в виде
Коэффициент линейной функции найдем по методу наименьших квадратов:
где Ryl – коэффициент корреляции между случайными величинами Y и L; s y и s l – среднеквадратические отклонения величин Y и L.
где
Среднее значение пробега находим по формуле
Среднее значение величины Y находим по формуле
Свободный член уравнения
Коэффициент корреляции используется в теории вероятностей для характеристики тесноты связи между случайными величинами Y и L:
где a 2,1(Y, L) – второй смешанный начальный момент случайных величин Y и L. Второй смешанный начальный момент:
Если случайные величины Y и L связаны точной линейной зависимостью (14), то RyL = ± 1, причем знак «плюс» или «минус» берется в зависимости от того, положителен или отрицателен коэффициент В в уравнении (14). В общем случае, когда Y и L связаны произвольной вероятностной зависимостью, коэффициент корреляции может иметь значение в пределах: –1 ≤ RyL ≤ +1. (23) Расчет коэффициентов парной регрессии производится на ПЭМ по приведенному на рис. 7 алгоритму программы. На основании выполненных расчетов коэффициентов парной регрессии необходимо построить эмпирические и аналитические зависимости среднего значения и среднеквадратического отклонения от пробега контролируемого параметра изнашиваемой детали ЭПС (рис. 7 и 8).
Рис. 7. Алгоритм программы расчета коэффициентов парной регрессии
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 399; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.142.248 (0.007 с.) |



 , (11)
, (11) , (12)
, (12)
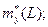

 . (14)
. (14) (15)
(15) ; (16)
; (16) , (17)
, (17) – среднее значение пробега L;
– среднее значение пробега L; – среднее значение величины Y.
– среднее значение величины Y.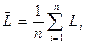 . (18)
. (18)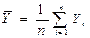 . (19)
. (19) . (20)
. (20) , (21)
, (21) (22)
(22)



