
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерпретация и анализ полученных результатов⇐ ПредыдущаяСтр 24 из 24
Полученная таким образом систематизация губерний Европейской части России может дать объяснения тех революционных событий, которые начались с малоземельных губерний (Московская, Петербургская) и которые разрушили Российскую империю. Действительно, если бедные губернии объединить с тяготеющими к бедным, то получим 62 % губерний по экономическому признаку количества десятин земли на душу относились к потенциально неблагополучным губерниям. В таких условиях лозунг большевиков – «земля народу» был брошен на неблагополучную среду и привел к разрушительным последствиям для России. Далее число бедных и богатых губерний оказалось равным, но в число неблагополучных губерний вышли густонаселенные Московская и Петербургская губернии, в которых, кроме того, была сосредоточена демократически настроенная интеллигенция и студенчество. Из истории также известно, что в период гражданской войны (1917-1920г.г.) в России такая богатая губерния как Донская была оплотом казачества, которое активно сопротивлялось установлению Советской власти на этой территории.
Лабораторная работа № 18. Метод Эйлера приближённого интегрирования дифференциального уравнения у' = f (х,у).
Начало численным методам интегрирования задачи Коши дифференциальных уравнений было положено Л. Эйлером в 1768г. В дальнейшем метод Эйлера усовершенствовался и уточнялся. Основной недостаток этих методов – их невысокая точность. Метод Эйлера – одношаговый методы не требуют предварительного построения начала таблицы значений приближенного решения, что дает возможность проводить вычислительный процесс с естественными начальными условиями и переменным шагом...
Рассматриваемые методы приближенного интегрирования ДУ основаны на тождестве: Пользуясь какой-либо квадратурной формулой для вычисления интеграла, получим различные формулы численного решения ДУ. Метод Эйлера заключается в том, что интегральную кривую, проходящую через точку (хоуо), заменяют ломаной, каждое звено которой проведено по направлению поля, определённого уравнением у' = f (х,у) в начальной точке этого звена. Иными словами, от предыдущей вершины ломаной к последующей двигаются по касательной к интегральной кривой, проведённой через начальную точку каждого звена.
Предположим, что нас интересует решение, отвечающее отрезку [хо,b]. Разделим его на п равных частей
тогда ломаная Эйлера определится вершинами
где
Расчёт ведётся по следующей схеме:
С увеличением числа делений, т.е. с уменьшением шага h, последовательность ломаных Эйлера как угодно близко приближается к искомой интегральной кривой. Но при этом увеличивается время вычислений и возрастает погрешность за счет ошибок округления. На практике задачу решают несколько раз, постепенно уменьшая шаг до тех пор, пока отклонения вычисленных значений функции для одних и тех же значений аргумента не станут пренебрежимо малы с точки зрения вычислителя.
Пример. Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением Ограничиться отысканием первых 10 значений y. Ход работы. 1. Включите компьютер, нажмите кнопку Пуск 2. В ячейку A1 введите значение 0. 3. Используя автозаполнение введите значения в ячейки А2 - А6.
4. В ячейки В1 – Е1 введите заголовки: 5. В ячейку В2 введите значение Х0. 6. В ячейку В3 введите формулу =B2+0,1 и далее продолжите автозаполнением до ячейки В11, заданный шаг h=0,1. 7. В ячейку С3 введите значение y0. 8. В ячейку С3 введите формулу =C2+0,1*(2*B2-C2) и далее автозаполнением до ячейки С11. 9. В меню Формат ячейки, на вкладке Число выберите Числовой формат, и кол-во знаков после запятой 2. Щелкните ОК. 10. В ячейке D2 вводим: =2*B2-C2 и делаем автозаполнение до D10.
11. В ячейке E2 вводим формулу: =0,1*(2*B2-C2) и делаем автозаполнение до E10 12. Выбираем Формат - Диаграммы. Выберите тип График с накоплением и нажмите Далее. 13. Укажите диапазон от C2 до C11 и ряды в столбцах. 14. Далее выбираем вкладку Ряд. Введите в поле Подписи оси X промежуток от B2 до B11. Нажмите Далее. 15. Сделайте все необходимые подписи к диаграмме. Нажмите Далее.
16. Нажмите Готово.
17.
Для повышения точности расчета уменьшим шаг вычислений. Выполните пп. 1-15 с заданным шагом Вычисления проводить в ячейках, начиная с F1. Постройте график. Найдем точное решение данного уравнения:
Данное уравнение является линейным неоднородным дифференциальным уравнением первого порядка. Общее решение линейного однородного уравнения:
Где С – произвольная постоянная. Общее решение неоднородного уравнения находим, исходя из общего решения соответствующего однородного уравнения методом Лагранжа, варьируя произвольную постоянную, т.е. полагая:
Тогда искомое общее решение линейного неоднородного уравнения имеет вид:
Используя начальное условие y(0) = 0, получим:
Следовательно, искомое частное решение имеет вид:
График точного решения имеет вид:
Для построения графика точного решения в ячейку Е2 введите формулу (*), используйте автозаполнение. По данным столбца Е постройте график, сравните приближенное решение дифференциального уравнения с точным.
По таблице 1 сравните приближенное значение функции y с точным решением в зависимости от величины шага h.
Задание Задача 1. Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением шаг h=0,1; 0,05. Задача 2. Методом Эйлера найти 10 значений функции y, определяемой уравнением y`=x+y, при начальном условии y(0)=1, полагая h=0,1; 0,05. Задача 3. Методом Эйлера найти 10 значений функции y, определяемой уравнением Задача 4. Методом Эйлера найти 10 значений функции y, определяемой уравнением Задача 5. Методом Эйлера найти численное решение уравнения Задача 6. Методом Эйлера найти численное решение уравнения
Список литературы 1. Кострикин А.И. Введение в алгебру. Основы алгебры: Учебник для вузов. - М.: Физматлит, 1994. - 320 с. (семестр 1, лекция 1-6) 2. Фомин Г.П. Математические методы и модели в коммерческой деятельности: Учебник. - М.: Финансы и статистика, 2001. - 544с. (семестр 1, лекция 7-8) 3. Бубнов В.А. Решение логических задач с помощью операций алгебры Жегалкина. Сб. Информационные технологии в предметной области. Вып. 1/ Отв. ред. проф. Бубнов В.А. _ М.: МГПУ, 2002. - с.5-16 (Семестр 1, лекция 9-10) 4. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Том 1. СПб.: Издательство "Лань", 1997. - 608с. (Семестр 1, лекция 11-12, 15-17, семестр III, лекции 1-13) 5. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Том 2. СПб.: Издательство "Лань", 1997. - 800с. (Семестр 1, лекция 16-17, семестр III, лекции 2-4) 6. Малькин В.И. Математика в экономике: Учебное пособие. - М.: ИНФРА-М, 2002. - 352 с. (Семестр 1, лекция 13) 7. Атанасян С.Л. Геометрия: Учебное пособие, ч 1,2. М.: МГОПИ, 1993. (Семестр 2, лекция 3-5, 7-8, 10-11) 8. Лаптев Г.Ф. Элементы векторного исчисления. -М.: ФИзматлит,1975. - 336с. (Семестр 2, лекция 3-4, 13-16) 9. Гмурман В.Е. Теория вероятностей и математическая статистика: Уч. пособие для вузов. М.: Высш. шк., 1977. -340с. (Семестр 4, лекции 5-17)
10. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х частях. Ч. 1, 2. Уч. пос. для ВТУЗов. 5 изд., испр. М.: Высш. шк., 1996. (Пособие для практических занятий) 11. Бубнов В.А., Мелещеня И.Н. Высшая математика. Программа и методические указания для студентов экономического факультета, обучающихся по специальности 061100 «менеджмент организации» Под ред. В.А. Бубнова. – М.: МГПУ 2005. 225с.
Дополнительная литература 1. Александров П.С. Лекции по аналитической геометрии. М.: Изд. "Наука", 1966 -912с. 2. Абчук В.А. Экономико-математические методы. СПб.: Союз, 1999 -320с. 3. Фомин Г.П. Математические методы и модели в комерческой деятельности: Учебник. М.: Финансы и статистика, 2001. 544с. 4. Малыхин В.И. Математика в экономике: учебное пособие. - М.: ИНФРА-М. 2002. -352с.
Программа: 2 Учебный план. 8 Приложение 1. 14 Домашнее задание № 1. Определители. 14 Домашнее задание №2 Матрицы и операции над ними. 18 Домашнее задание №3. Системы линейных алгебраических уравнений. 27 Домашнее задание №4 Область определения. Частные производные. Производная по направлению. Градиент. Дифференциал. 34 Домашнее задание №5. Производные и экстремумы функций. 36 Домашнее задание №6. Теория множеств. 37 Домашнее задание №7. Математическая логика. 40 Домашнее задание №8. Теория вероятности и математическая статистика. 42 Домашнее задание №9. Сетевое планирование и управление. 44 Домашнее задание №9. Линейное программирование. 50 Приложение 2. 52 Семестр I. 52 Лабораторная работа №1. Макрокоманды программы Microsoft Excel 2003. 52 Лабораторная работа №2. Определители 3-го порядка и их вычисление. 79 Лабораторная работа №3. Вычисление определителей 4-го порядка разложением по элементам любой строки. 85 Лабораторная работа №4. Вычисление определителей 4-го порядка разложением по элементам любого столбца. 90 Лабораторная работа №5. Словесные алгоритмы линейной алгебры и их реализация в программе Excel. 94 Лабораторная работа №6. Вычисление ранга матрицы. 99 Лабораторная работа №7. Умножение матриц. 104 Лабораторная работа №8. Вычисление обратной матрицы. 110 Лабораторная работа №9. Решение систем линейных уравнений по формуле Крамера. 116 Лабораторная работа № 10. Решение систем линейных уравнений в матричном виде. 120 Лабораторная работа № 11. Решение систем линейных уравнений. 123 с четырьмя неизвестными методом Гаусса. 123
Лабораторная работа № 12. Нахождение собственных значений линейного оператора. 127 Лабораторная работа № 13. Логические задачи в алгебре Буля. 133 Лабораторная работа № 14. Логические задачи в алгебре Жегалкина. 146 Лабораторная работа № 15. Нахождение корней уравнения f(x)=0. 156 Лабораторная работа № 16. Задачи линейного программирования. 167 Семестр II. 174 Лабораторная работа № 2. Изучение числовых последовательностей. 174 Лабораторная работа № 6. Численное дифференцирование степенной функции. 186 Лабораторная работа №10. Приближенное вычисление определенных интегралов. Формула Симпсона. 196 Лабораторная работа№16. Закон устойчивости частот. 203 Лабораторная работа №17. Анализ экономико-исторических явлений статистическими моделями 215 Лабораторная работа № 18. Метод Эйлера приближённого интегрирования дифференциального уравнения у' = f (х,у). 228 Список литературы.. 233 Дополнительная литература. 234
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 140; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.240.142 (0.05 с.) |

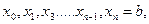
 (k= 0, 1, 2,..., п),
(k= 0, 1, 2,..., п), ,
, 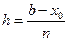 - шаг деления,
- шаг деления,




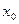

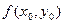



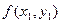
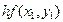




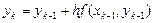


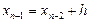
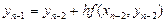

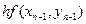
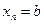
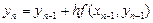
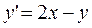 , при начальном условии y(0)=0, шаг h = 0,1.
, при начальном условии y(0)=0, шаг h = 0,1. , выберите программу Microsoft Excel.
, выберите программу Microsoft Excel.




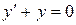 получается разделением переменных
получается разделением переменных
 где С(x) – некоторая, дифференцируемая функция от x.
где С(x) – некоторая, дифференцируемая функция от x.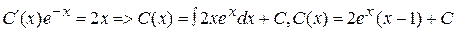

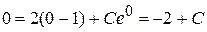

 . (*)
. (*)


 , при начальном условии y(0)=1
, при начальном условии y(0)=1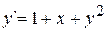 , при начальном условии y(0)=1, полагая h=0,1; 0,05.
, при начальном условии y(0)=1, полагая h=0,1; 0,05. , при начальном условии y(0)=0, полагая h=0,1; 0,05.
, при начальном условии y(0)=0, полагая h=0,1; 0,05. при начальном условии y(2)=4, полагая h=0,1; 0,05.
при начальном условии y(2)=4, полагая h=0,1; 0,05. на отрезке [0,1] при начальном условии y(0)=1, полагая h=0,2;0,1.
на отрезке [0,1] при начальном условии y(0)=1, полагая h=0,2;0,1.


