
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Согласно формуле (29.15), получим
j у/1 — х t V=Qzdxdy=^dx J (3— х— y)dy= J j^3x— xy —yj dx= yj 1 x2 П-Xi
= I (бл/l — x2 — 2x yj 1 —x2)dx.
____ у х 0 — x2dx=-arcsin x+-y/l — х2, 41. Вычислить объем шара радиуса R.
силу симметрии сферы относительно начала координат вычислим 1 /8 объема шара, расположенную в I октанте. Проекция части сферы, принадлежащей I октанту, на плоскость хОу есть 1/4 часть круга х2 +y2 = R2, ограниченная осями Ох и Оу. Для упрощения вычислений интеграла перейдем к полярным координатам. Так как x=rcoscp, >>=rsin(p, то x2+y2 = r2, r=R. Полярный угол изменяется от 0 до тс/2. Область D в полярных координатах запишем в виде системы неравенств 0<ф^я/2, О^г^Л.
о Вычислим внешний интеграл:
1 4 Значит, F=8 -nR3=-nR3. # 6 3 42. Вычислить объем тела, ограниченного поверхностями z=9 — x2 —у2, х2 + у2 — 2у = 0, z=0. О Данное тело есть вертикальный цилиндр, ограниченный сверху параболоидом z=9 —х2—у2, сбоку цилиндром x2-hy2—2у=0, снизу кругом х2 + у2—2у=0. Так как область интегрирования является кругом, а подынтегральная функция зависит от х2 +у2, то перейдем к полярным координатам. Уравнение окружности примет вид r2cos29 + r2 sin29 — 2rsin9=0 или т2—2т sin ф = 0, откуда ^=0, r2 = 2sin9. Полярный угол ф изменяется от 0 до п. Область D запишется в виде системы неравенств О^ф^тг, 0^г^2sinф, а подынтегральная функция примет вид z=9—(х2+>>2)=9—г2. Используя формулу (29.15), получим V=jjzdxdy=jj(9-r2)rdrdq>=jdq> J (9r-r3)<fr=|j^-S'”’rf(p = D D 0 0 0 =|[18sin29-4sin4<p]</<p=|^181 c°s2?_4^] ^s2(p^ ^dq> = 0 0 я = J[9“ 9c°s2cp —1 + 2cos 2ф—сов22ф]^ф = я = jj^8 - 7 cos 2cp - * + C°S 4<P j cftp = 7, 5 (куб.ед.). • о 43. Вычислите объемы тел, ограниченных заданными поверхностями: 1) z = 6, у=х2, у=4, х=0, z=0; 2) z = 3 — x—y, х=0, у = х2 + \, у = 2, z = 0; 3) z—4—х2 —у2, х= ±2, у=±2, z = 0; 4) z = 4x+ 1, у=х29 х=0, у = 4, z = 0; 5) z = 4 —х2, х+>> —4 = 0, х=0, jf = 0, z = 0; 6) z = 2—x, j;2 = 9x, >>=3x2, z = 0; 7) z=x2+}'2, x+>> = 2, x = 0, y=0, z=0; 8) z=x2+y2, x=0, x=3, 7 = 0, 7 = 2, z=0. 44. Вычислите объемы тел, ограниченных заданными поверхностями (для вычисления интегралов используйте полярные координаты): 1) z—16 —(х2+у2), z = 0; 2) z = n/x2+t2, х2+>>2 = 9, z = 0; 3) z = x2+y2, x2+j>2 = 4, y=x9 y — у/ Зх, z = 0; дуга окружности x2+j>2 = 4 лежит в I квадранте; 4) z = 6 — х2— у2, x2-hy2 = 4, z = 0; 5) z = x2+y29 x2-h72 + z2=12, z=0; 6) z=12 —x2—72, z = 3. ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПОВЕРХНОСТИ Если поверхность задана уравнением z=f(x, у) и проектируется в область D плоскости хОу (2=0), то площадь S поверхности вычисляется по формуле
s* Я D5**- <29-,б) D (хОу) Если поверхность проектируется на плоскость yOz (х=0), то уравнение поверхности следует решить относительно переменной х и формула примет вид s= II >жщ D iyOz) Если поверхность проектируется на плоскость хОу(у= 0), то уравнение поверхности следует решить относительно переменной у и формула примет вид s‘ II(29,8> D ( xOz) 45. Вычислить площадь треугольника, образованного при пересечении плоскости x+3y + 2z=6 с координатными плоскостями. О Найдем отрезки, отсекаемые на координатных осях данной плоскостью:
6 + 2+3=1’ х=6, у—2, z—3 (рис. 217). Чтобы воспользоваться формулой (29.16), решим уравнение данной плоскости относительно переменной z и найдем частные 1 1 3 производные: z=3--x—-y, dz 1 dz 3 dx 2’ dy 2 При z=0 имеем x+3y=6, откуда у = 2—-x; следовательно, в плоскости z=0 область D запишется в виде системы неравенств О^х^б, Тогда 5= Я >/1+(4У+Н) dxdy=\dx { D (хОу) о О О ^x^rfx=3N/l4 (кв. ед.). • О 46. Вычислить площадь части поверхности цилиндра х2+у2 = 16, заключенной между плоскостями z = 0, z = 4x, у=0. О Искомая поверхность лежит в I октанте (рис. 218). Проекция поверхности на плоскость xOz (у=0) есть прямоугольный треугольник, в котором ОЛ=х=4 и уравнение гипотенузы О В имеет вид z=4x. Следовательно, область D в плоскости xOz определяется системой неравенств 0<;с<4, 0<z<4a:.
|
||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 389; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.98.166 (0.01 с.) |
 1
1 Первый интеграл вычисляется по формуле
Первый интеграл вычисляется по формуле
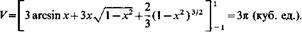 О Из уравнения сферы x2+y2+z2 = R2 находим z=^/R2 — (х2+у2). В
О Из уравнения сферы x2+y2+z2 = R2 находим z=^/R2 — (х2+у2). В
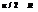




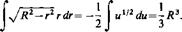


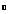 Согласно формуле (29.15), получим
Согласно формуле (29.15), получим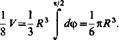 о
о
 х у z л
х у z л


