
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операции над высказываниями (сложные высказывания)Стр 1 из 7Следующая ⇒
Используя союзы и словосочетания «и», «или», «не (нет)», «следует (если, …, то….)», «тогда и только тогда, когда» можно из простых высказываний составлять более сложные, истинность которых определяется истинностью составляющих высказываний. 1. Дизъюнкция: А 2. Конъюнкция: А 3. Отрицание: 4. Импликация: А 5. Эквивалентность: А
Структура теорем (утверждений) Прямые и обратные (по отношению друг к другу) теоремы иллюстрирует следующий Пример. Предикаты: Прямая теорема: В этом случае говорят, что Обратная теорема: Условие Законы отрицания сложных высказываний. Эти законы могут применяться при построении противоположного высказывания при доказательстве «от противного». Доказываются построением таблиц истинности для правой и левой части. 1. 2. 3. 4. 5.
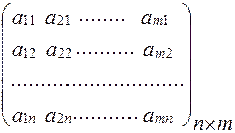
Раздел II. Основы линейной алгебры Матрицы Матрицей называется прямоугольная таблица чисел. Обозначаются прописными буквами А, В, С, ….. Общий вид матрицы, содержащей m строк и n столбцов: (1) Внизу справа при необходимости подписываются размеры матрицы: m – количество строк, n – столбцов. Числа
В дальнейшем будет видно, что матрицы (так же как и числа) можно вычитать, складывать, перемножать. Поэтому среди матриц есть аналоги нуля и единицы. Нулевой матрицей называется матрица, все элементы которой равны нулю. Она имеет следующий вид и обозначение: Если в матрице (1) поменять местами строчки и столбцы (т.е. первую строчку сделать первым столбцом, вторую строку – вторым столбцом и т.д.), то полученная матрица носит название транспонированной по отношению к исходной матрице и обозначается
Квадратная матрица – матрица, число строк и столбцов у которой совпадают. Общий вид квадратной матрицы: (2) Числа Единичной называется такая квадратная матрица, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю: (3) Е =
Операции с матрицами
1. Сумма матриц: А + В. Складывать можно только матрицы одного размера. При сложении двух матриц одного размера получается матрица того же размера, элементы которой равны сумме элементов слагаемых матриц, стоящих на соответствующих местах. Пример. Пусть
Аналогично определяется вычитание матриц:
2. Умножение числа на матрицу. При умножении числа на матрицу каждый ее элемент умножается на это число. Пример.
Матричные уравнения Это уравнения, в которых неизвестной является матрица. Пример. Даны матрицы
3. Умножение матриц: Далеко не все матрицы можно перемножать. Матрицы A и B (порядок следования важен!) называются согласованными, если число столбцов матрицы A равно числу строк матрицы B. Таким образом, если порядок матрицы A равен m × p, то порядок согласованной с ней матрицы B должен быть равен p × n. Перемножать можно только согласованные матрицы (отметим, что квадратные матрицы одного порядка всегда согласованы).
Например, если требуется получить элемент Рассмотрим конкретные матрицы
Пример. Пусть
А·Е = Е·А = А. Пример (практический, использующий умножение матриц). В таблице указано количество единиц продукции, отгружаемой ежедневно на молокозаводах 1 и 2 в магазины М1, М2 и М3, причем доставка единицы продукции с каждого молокозавода в магазин М1 стоит 50 денежных единиц, в магазин
Решение. Обозначим через А матрицу, составленную в соответствии с данной таблицей, а через В − матрицу-столбец, характеризующую стоимость доставки единицы продукции в магазины, т.е., Пример. Даны матрицы Решение. Найдем сначала матрицу
Определители матриц
Для каждой квадратной матриц вводится важная ее числовая характеристика, называемая определителем этой матрицы. Правило, по которому по элементам данной квадратной матрицы произвольного порядка вычисляется ее определитель, достаточно сложно, поэтому будем давать это правило «постепенно», повышая порядок определителя. Пока же ограничимся таким неконструктивным определением.
Каждой квадратной матрице можно по некоторому (вот в чем неконструктивность!) правилу поставить в соответствие число, которое называется определителем данной матрицы. Для определителя квадратной матрицы A, общий вид которой дан в (2), применяются различные обозначения. Укажем наиболее употребительные:
Будем подбираться к строгому определению определителя, рассмотрев это правило последовательно для определителей матриц 1 -го, 2 -го и 3 -го порядков. Определителем матрицы 1 -го порядка называется число, равное единственному имеющемуся у матрицы числу − матричному элементу этой матрицы. Определение настолько простое, что нет необходимости иллюстрировать его примером. Определитель матрицы второго порядка. Если Например, Рассмотрим определитель матрицы третьего порядка Минором элемента матрицы Алгебраическим дополнением элемента матрицы (3) Поскольку число (–1) в целой степени принимает всего два значения (1 – если показатель степени есть четное число и (–1) – если нечетное), то алгебраическое дополнение элемента матрицы либо ничем не отличается от минора этого элемента (если сумма его нижних индексов – т.е. сумма номеров строки и столбца – есть четное число) или отличается от минора только знаком (если сумма нижних индексов нечетна).
Пример. Найти миноры и алгебраические дополнения всех элементов матрицы (4) А = Решение. Сначала ищем миноры всех элементов. М11= М21= М31= Учитывая формулу (3) и приведенные ниже пояснения для этой формулы, получаем следующие алгебраические дополнения
Для матрицы (4) для каждой строки (и столбца) проделаем: составим сумму попарных произведений ее (его) элементов на их алгебраические дополнения. Например, для второго столбца: Определителем квадратной матрицы (любого порядка!) называется число, равное сумме попарных произведений элементов любой строки (столбца) на их алгебраические дополнения. Поэтому для матрицы (4) по этому определению: D = Для вычисления определителя именно третьего порядка есть упрощенная (по сравнению с общим определением) формула
которая схематически (для запоминания) записывается так:
– последние 3 слагаемые (берутся со знаком −)
Пример. Найдем по упрощенной схеме определитель матрицы (4).
Как и следовало ожидать, результат получился тот же, что и ранее. Для вычисления определителей матриц более высокого (чем третьего) порядка упрощенной схемы нет, поэтому используется только метод, данный в определении: выбирается строка или столбец матрицы и вычисляется сумма попарных произведений соответствующих элементов матрицы на их алгебраические дополнения. При этом вычисление алгебраических дополнений – самый хлопотный этап. Но поскольку строку (или столбец) можно выбирать произвольно (результат от этого не зависит), то проще выбрать ту, среди элементов которой как можно больше нулевых. При этом алгебраические дополнения нулевых элементов можно не считать, так как при составлении упомянутой выше суммы попарных произведений соответствующие слагаемые все равно обратятся в ноль. Пример. Вычислить определитель 4-го порядка: Решение. Самое большое количество нулей в любой из строк или столбцов равно 2. Поэтому для вычисления определителя выбираем любую строку или столбец с двумя нулями. Выберем, например, первый столбец (при этом говорят, что определитель будет разлагаться по первому столбцу):
Появившиеся два определителя 3-го порядка можно считать по приведенной выше упрощенной схеме. Если среди элементов матрицы нулей мало (или нет вовсе), то можно специальными действиями привести определитель к такому виду, у которого есть строка (или столбец), в которой отличен от нуля только один элемент. После этого определитель легко вычисляется разложением по этой строке (столбцу). Привести определитель к такому виду помогают свойства определителей, рассмотренные ниже.
Свойства определителей 1. Если у определителя какая-либо строка (столбец) состоит из нулей, то определитель равен нулю. 2. Если какие-либо две строки (два столбца) определителя равны или пропорциональны (т.е. элементы одной строки (столбца) получаются умножением элементов другой строки (столбца) на одно и то же число), то определитель равен нулю. 3. Если две строки (два столбца) поменять местами, то определитель изменит знак. 4. Общий множитель элементов любой строки или столбца можно выносить за знак определителя. 5. Если к элементам одной строки (столбца) прибавить соответствующие элементы другой строки (столбца), предварительно умноженные на одно и то же число, то определитель не изменится. Справедливость этих свойств непосредственно проверяется для определителей второго и третьего порядка. Общее доказательство достаточно громоздко. Как сказано выше, с помощью этих свойств можно привести определитель к такому виду, у которого есть строка (или столбец), в которой отличен от нуля только один элемент. Для приведения определителя к такому виду необходимо: 1) Вынести общие множители (если таковые имеются) из строк или столбцов за знак определителя (свойство 4.). Это позволяет уменьшить элементы определителя (что облегчает его дальнейшее вычисление), а также, возможно, получить элементы, равные 1 или (−1), что поможет выполнению следующего пункта. 2) Выбрать строку (или столбец), в которой есть элемент 1 или (−1) (если такие строки или столбцы есть) и с помощью этого элемента (и последнего свойства определителей) обнулять остальные элементы выбранной строки или столбца. Иллюстрирует сказанное следующий Пример. Обратная матрица Рассмотрим обычное простейшее уравнение Матрица Из определения следует, что обратная матрица B будет квадратной матрицей того же порядка, что и матрица A (иначе, как несложно убедиться, одно из произведений
Для всех ли обратных матриц существуют обратные? Как было сказано раньше, даже не для всех чисел существует обратное: для числа 0 обратного нет. Похожая ситуация наблюдается и с матрицами. Матрица называется вырожденной, если ее определитель = 0. Справедлива следующая Теорема. Обратная матрица для квадратной матрицы A вида (2) существует тогда и только тогда, когда матрица A невырожденная. В этом случае обратная матрица единственна и представляется в виде (5) где Формула (5) обосновывает следующий алгоритм вычисления обратной матрицы (на примере матрицы размера 3х3) для матрицы
1. Вычисляем определитель матрицы 2. Вычисляем алгебраические дополнения всех ее элементов 3. Составляем так называемую «союзную» матрицу, заменяя элементы исходной матрицы их алгебраическими дополнениями и транспонируя получившуюся матрицу:
4. Составляем обратную: Пример. Найти обратную для матрицы Решение. Воспользуемся тем, что ранее (в параграфе «Определители матриц») для этой матрицы уже были вычислены определитель и алгебраические дополнения всех элементов. Поэтому результаты первых двух пунктов приведенной выше схемы уже есть. 1. 2. 3. «Союзная» матрица: 4. Составляем обратную: Ответ: Можно было произвести умножение числа Наиболее просто искать по приведенной схеме обратную матрицу для матриц второго порядка. Пусть дана в общем виде матрица второго порядка 1. D= 2. 3. 4. Таким образом, обратная для матрицы второго порядка (5а) Пример. Найти для матрицы Решение. Определитель (5б)
Системы линейных алгебраических уравнений (СЛАУ) Многие практические задачи приводят к необходимости решения такого рода систем уравнений. Приведем пример такой задачи. Пример (прогноз выпуска продукции по запасам сырья). Предприятие выпускает 3 вида продукции, используя сырье трех типов. Характеристики производства понятны из следующей таблицы:
Требуется определить объем выпуска продукции каждого вида при условии полного расходования запасов сырья. Решение. Обозначим через
Можно непосредственной подстановкой убедиться, что числа Система линейных алгебраических уравнений (сокращенно СЛАУ) из m уравнений с n неизвестными имеет вид (6) Числа Набор чисел Совместная система – имеет хотя бы одно решение. Совместные системы могут быть определенными и неопределенными. Определенная система – имеет единственное решение. Неопределенная – имеет более одного решения. Специфика систем линейных уравнений вида (6) такова, что если эта система имеет более одного решения, то она имеет бесконечное число решений. Приведем примеры. Система Система
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.160.156 (0.11 с.) |
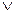 В. Читается: А или В. Высказывание А
В. Читается: А или В. Высказывание А 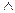 В. Читается: А и В. Высказывание А
В. Читается: А и В. Высказывание А 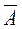 (или
(или 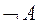 ). Читается: не А. Высказывание
). Читается: не А. Высказывание 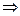 В. Читается: из А следует В. Высказывание А
В. Читается: из А следует В. Высказывание А  В. Читается: А тогда и только тогда, когда В. Высказывание А
В. Читается: А тогда и только тогда, когда В. Высказывание А 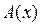 – треугольник х – правильный,
– треугольник х – правильный, 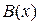 – углы треугольника х равны. Построим предикаты
– углы треугольника х равны. Построим предикаты 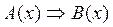 и
и 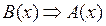 .
.
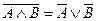
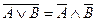
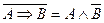 (основание метода доказательства «от противного»)
(основание метода доказательства «от противного»)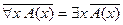

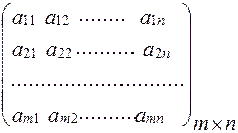
 , составляющие матрицу, называются элементами матрицы. Матричные элементы обычно обозначаются той же буквой (только строчной), что и сама матрица, а индексы показывают место элемента матрицы в матрице: первый индекс указывает номер строки, а второй – номер столбца, на пересечении которых находится данный матричный элемент. Например, для матрицы
, составляющие матрицу, называются элементами матрицы. Матричные элементы обычно обозначаются той же буквой (только строчной), что и сама матрица, а индексы показывают место элемента матрицы в матрице: первый индекс указывает номер строки, а второй – номер столбца, на пересечении которых находится данный матричный элемент. Например, для матрицы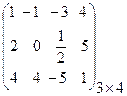 элементы
элементы 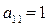 ,
, 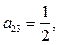 …..
…..
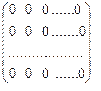 .
.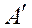 или
или 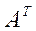 :
:
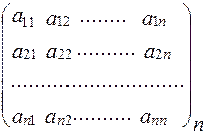
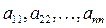
 называются главной диагональю квадратной матрицы.
называются главной диагональю квадратной матрицы.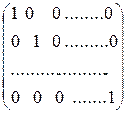 .
.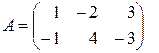 ,
, 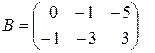 . Тогда
. Тогда =
= 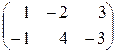 +
+ 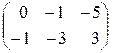 =
= 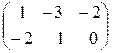
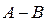 =
= 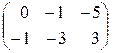 =
= 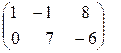 .
.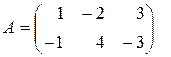 , тогда
, тогда 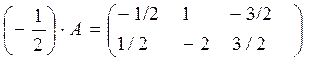 .
.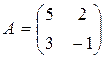 и
и 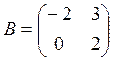 . Найти матрицу
. Найти матрицу 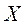 , удовлетворяющую следующему матричному уравнению
, удовлетворяющую следующему матричному уравнению 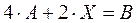 .
. . Затем действия, предписываемые этой формулой, выполняем по правилам действий с матрицами. Решая обычным способом уравнение
. Затем действия, предписываемые этой формулой, выполняем по правилам действий с матрицами. Решая обычным способом уравнение 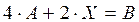 , получаем
, получаем 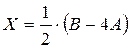 . По правилу умножения числа на матрицу
. По правилу умножения числа на матрицу 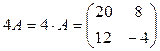 , по правилу вычитания матриц
, по правилу вычитания матриц 
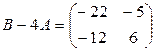 . Наконец, по правилу умножения числа на матрицу неизвестная матрица
. Наконец, по правилу умножения числа на матрицу неизвестная матрица 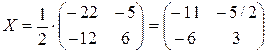 .
.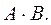
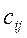 матрицы С равен сумме попарных произведений элементов i -ой строки матрицы А и j -го столбца матрицы В:
матрицы С равен сумме попарных произведений элементов i -ой строки матрицы А и j -го столбца матрицы В: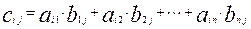
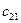 , то нужно вторую строку матрицы
, то нужно вторую строку матрицы 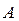 "умножить" на первый столбец матрицы
"умножить" на первый столбец матрицы 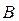 .
.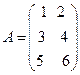 ,
, 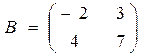 . Число столбцов матрицы
. Число столбцов матрицы 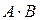 будет размера
будет размера 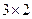 . Тогда по определению произведение этих матриц
. Тогда по определению произведение этих матриц 
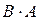 невозможно, т.к. матрицы B и A не согласованы. Отсюда следует, что если две матрицы можно перемножить в одном порядке, то это не означает, что их можно перемножать в другом порядке. Можно показать, что в общем случае, даже когда произведения
невозможно, т.к. матрицы B и A не согласованы. Отсюда следует, что если две матрицы можно перемножить в одном порядке, то это не означает, что их можно перемножать в другом порядке. Можно показать, что в общем случае, даже когда произведения  ,
, 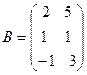 . Тогда
. Тогда 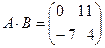 , а
, а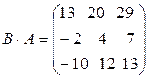 (проверьте!). Таким образом
(проверьте!). Таким образом 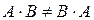 . Это не значит, что вообще не существует двух таких матриц А и В, для которых
. Это не значит, что вообще не существует двух таких матриц А и В, для которых 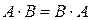 . Если для пары матриц А и В это свойство все же выполняется, то такие матрицы называются перестановочными (или коммутативными). Например, коммутативными будут матрицы А =
. Если для пары матриц А и В это свойство все же выполняется, то такие матрицы называются перестановочными (или коммутативными). Например, коммутативными будут матрицы А = 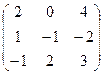 и В =
и В = 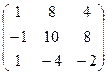 . Легко перемножением в том и обратном порядке убедиться, что
. Легко перемножением в том и обратном порядке убедиться, что 
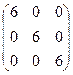 . Отметим, что квадратные матрицы можно перемножать только если они одного порядка. Можно указать одну особенную матрицу, которая перестановочна с любой квадратной матрицей (соответствующего порядка). Это введенная выше единичная матрица. Легко в общем виде показать, что для любой квадратной матрицы А имеет место:
. Отметим, что квадратные матрицы можно перемножать только если они одного порядка. Можно указать одну особенную матрицу, которая перестановочна с любой квадратной матрицей (соответствующего порядка). Это введенная выше единичная матрица. Легко в общем виде показать, что для любой квадратной матрицы А имеет место: ,
, 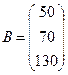 . Построим (пока чисто формально) произведение этих матриц − матрицу А·В:
. Построим (пока чисто формально) произведение этих матриц − матрицу А·В: 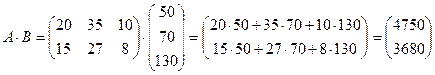 . По смыслу выполненных только что действий легко понять, что в данном случае произведение матриц А·В представляет собой матрицу затрат на перевозки. Итак, первый завод ежедневно тратит на перевозки 4750 денежных единиц, второй 3680 денежных единиц.
. По смыслу выполненных только что действий легко понять, что в данном случае произведение матриц А·В представляет собой матрицу затрат на перевозки. Итак, первый завод ежедневно тратит на перевозки 4750 денежных единиц, второй 3680 денежных единиц.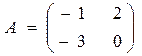 и
и  . Найти матрицу
. Найти матрицу 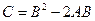 .
.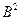 . По определению умножения матриц
. По определению умножения матриц 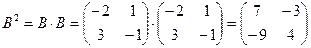 . Далее,
. Далее, 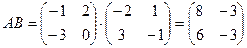 . По определению умножения числа на матрицу:
. По определению умножения числа на матрицу: 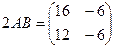 . Окончательно, по определению разности матриц:
. Окончательно, по определению разности матриц: 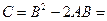
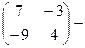
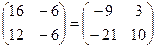 .
.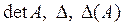 или развернутое, в котором перечисляются все элементы данной матрицы:
или развернутое, в котором перечисляются все элементы данной матрицы: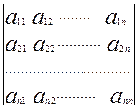 . Прямые черты, заменяющие круглые (матричные) скобки, указывают на то, что имеется в виду именно определитель матрицы, т.е. единственное число, а не сама матрица A.
. Прямые черты, заменяющие круглые (матричные) скобки, указывают на то, что имеется в виду именно определитель матрицы, т.е. единственное число, а не сама матрица A.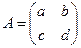 , то по определению
, то по определению 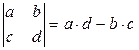
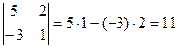 .
.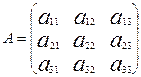 . Всё, что мы будем далее говорить для этой матрицы, справедливо и для квадратной матрицы любого порядка. Определение определителя матрицы содержит два новых понятия. Оказывается, для каждого элемента матрицы (а их всего 9) можно посчитать 2 числа, которые называются, соответственно, минором и алгебраическим дополнением этого элемента.
. Всё, что мы будем далее говорить для этой матрицы, справедливо и для квадратной матрицы любого порядка. Определение определителя матрицы содержит два новых понятия. Оказывается, для каждого элемента матрицы (а их всего 9) можно посчитать 2 числа, которые называются, соответственно, минором и алгебраическим дополнением этого элемента.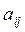 (обозначается
(обозначается 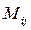 ) называется значение определителя матрицы, получающейся из данной матрицы вычеркиванием строки и столбца, на пересечении которых стоит данный элемент (т.е. вычеркиванием i -ой строки и j -го столбца).
) называется значение определителя матрицы, получающейся из данной матрицы вычеркиванием строки и столбца, на пересечении которых стоит данный элемент (т.е. вычеркиванием i -ой строки и j -го столбца).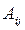 ) называется число, определяемое по формуле
) называется число, определяемое по формуле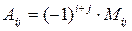 .
.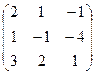 .
.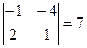 , М12=
, М12= 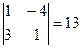 , М13=
, М13= 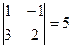 ,
,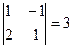 , М22=
, М22= 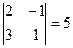 , М23=
, М23=  ,
, , М32=
, М32= 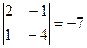 , М33=
, М33= 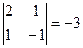 .
.

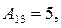
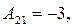

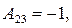
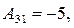

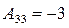 .
.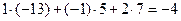 . Взяв любой другой столбец (или строку), получим то же самое число (для данной матрицы это (– 4)). Это общее свойство всех квадратных матриц − результат таких вычислений не зависит от того, какую строчку или столбец матрицы мы выбрали. Поэтому корректно следующее определение.
. Взяв любой другой столбец (или строку), получим то же самое число (для данной матрицы это (– 4)). Это общее свойство всех квадратных матриц − результат таких вычислений не зависит от того, какую строчку или столбец матрицы мы выбрали. Поэтому корректно следующее определение.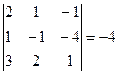 .
.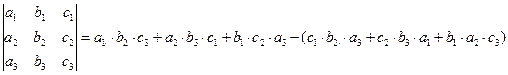 ,
,
 – первые три слагаемые (берутся со знаком +),
– первые три слагаемые (берутся со знаком +),
 .
.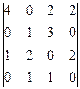 .
.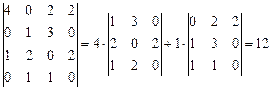 .
.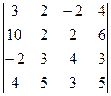 = {вынесем 2 из второй строки (свойство 4)} =
= {вынесем 2 из второй строки (свойство 4)} =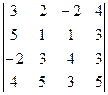 = {С помощью элемента а22=1 и свойства 5 обнуляем все элементы второй строки, кроме самого а22=1. Для этого а) прибавляем к 1 -му столбцу 2 -ой, умноженный поэлементно на (−5); б) прибавляем к 3 -му столбцу 2 -ой, умноженный на (−1); в) прибавляем к 4 -му столбцу 2 -ой, умноженный на (−3)} = 2 ∙
= {С помощью элемента а22=1 и свойства 5 обнуляем все элементы второй строки, кроме самого а22=1. Для этого а) прибавляем к 1 -му столбцу 2 -ой, умноженный поэлементно на (−5); б) прибавляем к 3 -му столбцу 2 -ой, умноженный на (−1); в) прибавляем к 4 -му столбцу 2 -ой, умноженный на (−3)} = 2 ∙ 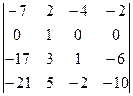 = {раскладываем определитель по второй строке} = = 2∙1∙(−1)2+2 ∙
= {раскладываем определитель по второй строке} = = 2∙1∙(−1)2+2 ∙ 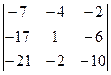 = {для облегчения вычисления определителя 3 -го порядка выносим (−1) из первых двух столбцов, а из третьего (−2) } =
= {для облегчения вычисления определителя 3 -го порядка выносим (−1) из первых двух столбцов, а из третьего (−2) } = 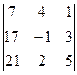 = {вычисляем определитель третьего порядка по упрощенной схеме}= −4∙{−35+34+222−(−21+42+340)}=−560.
= {вычисляем определитель третьего порядка по упрощенной схеме}= −4∙{−35+34+222−(−21+42+340)}=−560.  . Известно, что для его решения необходимо разделить обе части этого уравнения на 2. Деление на 2 можно представить как умножение на число
. Известно, что для его решения необходимо разделить обе части этого уравнения на 2. Деление на 2 можно представить как умножение на число 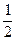 , которое, в свою очередь, может быть записано как
, которое, в свою очередь, может быть записано как 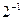 :
: 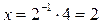 . Число
. Число 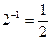 называется числом, обратным к числу 2, поскольку в произведении эти числа дают 1. В общем случае уравнение
называется числом, обратным к числу 2, поскольку в произведении эти числа дают 1. В общем случае уравнение 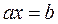 решается умножением обеих частей уравнения на число
решается умножением обеих частей уравнения на число 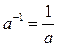 (если
(если 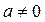 ), которое называется обратным к числу
), которое называется обратным к числу 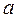 и определяется как число, дающее в произведении с
и определяется как число, дающее в произведении с 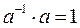 . Таким образом,
. Таким образом, 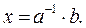 Напомним, что обратное число
Напомним, что обратное число  существует для всех чисел
существует для всех чисел 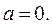 Сейчас мы по аналогии с обратным числом введем понятие обратной матрицы, которое нам поможет решать уже не одно уравнение, а целые системы уравнений определенного вида.
Сейчас мы по аналогии с обратным числом введем понятие обратной матрицы, которое нам поможет решать уже не одно уравнение, а целые системы уравнений определенного вида.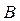 называется обратной матрицей для квадратной матрицы
называется обратной матрицей для квадратной матрицы 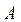 , если
, если 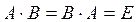 . Отметим, что в этом определении обратной матрицы недостаточно требовать, чтобы произведение матриц A и B в каком-либо одном порядке давало единичную матрицу, так как для матриц нет гарантии, что произведение этих матриц в другом порядке тоже даст единичную матрицу (в общем случае, как мы уже убеждались,
. Отметим, что в этом определении обратной матрицы недостаточно требовать, чтобы произведение матриц A и B в каком-либо одном порядке давало единичную матрицу, так как для матриц нет гарантии, что произведение этих матриц в другом порядке тоже даст единичную матрицу (в общем случае, как мы уже убеждались, 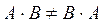 ).
).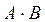 или
или 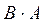 было бы не определено). Обратная матрица для любой матрицы A единственна (если существует) и обозначается
было бы не определено). Обратная матрица для любой матрицы A единственна (если существует) и обозначается 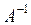 по аналогии с обратными числами. Таким образом, если
по аналогии с обратными числами. Таким образом, если 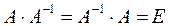 .
.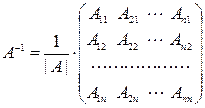 ,
,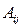 − алгебраические дополнения элементов
− алгебраические дополнения элементов 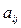 исходной матрицы.
исходной матрицы.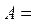
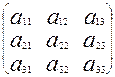 .
.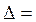
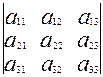 .
.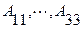 .
.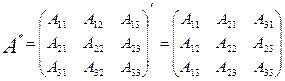 .
.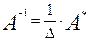
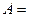
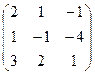 .
.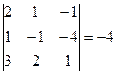 .
.
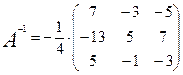 .
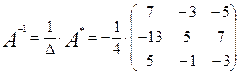
.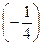 на матрицу и получить обратную матрицу в обычном матричном виде
на матрицу и получить обратную матрицу в обычном матричном виде 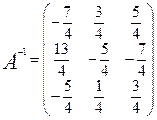 . При этом матрица уже не выглядит столь компактно, да и дальнейшие действия с ней (например, при решении систем линейных уравнений) производить уже не столь удобно. Поэтому обычно обратную матрицу оставляют в том виде, в котором она дана в Ответе.
. При этом матрица уже не выглядит столь компактно, да и дальнейшие действия с ней (например, при решении систем линейных уравнений) производить уже не столь удобно. Поэтому обычно обратную матрицу оставляют в том виде, в котором она дана в Ответе.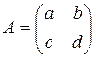 . Построим обратную матрицу по приведенной выше схеме.
. Построим обратную матрицу по приведенной выше схеме.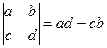 .
.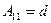 ,
, 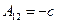 ,
, 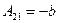 ,
, 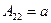 .
.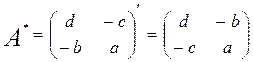 .
.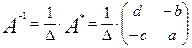 .
.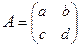 имеет вид:
имеет вид: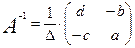 , где
, где 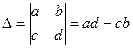 .
.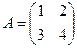 обратную матрицу.
обратную матрицу. . По формуле (5а)
. По формуле (5а)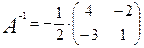 .
.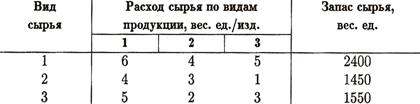
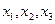 искомые объемы выпуска (в соответствующих единицах) продукции 1 -го, 2 -го и 3 -го вида соответственно. Тогда для того, чтобы при выпуске такого объема продукции было израсходовано все сырье 1-го типа, должно выполняться равенство:
искомые объемы выпуска (в соответствующих единицах) продукции 1 -го, 2 -го и 3 -го вида соответственно. Тогда для того, чтобы при выпуске такого объема продукции было израсходовано все сырье 1-го типа, должно выполняться равенство: 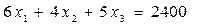 . Аналогичные «балансовые» соотношения для сырья оставшихся типов:
. Аналогичные «балансовые» соотношения для сырья оставшихся типов:  и
и 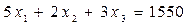 . Таким образом, необходимо найти три числа
. Таким образом, необходимо найти три числа 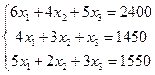
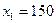 ,
, 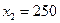 и
и 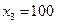 являются решением этой системы (при подстановке в нее дают верные числовые равенства), а потому предприятие выпускает 150 единиц продукции 1- го вида, 250 единиц продукции 2- го вида и 100 единиц 3- го вида.
являются решением этой системы (при подстановке в нее дают верные числовые равенства), а потому предприятие выпускает 150 единиц продукции 1- го вида, 250 единиц продукции 2- го вида и 100 единиц 3- го вида.
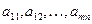 являются коэффициентами при искомых неизвестных
являются коэффициентами при искомых неизвестных 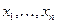 в уравнениях системы. Первый индекс чисел
в уравнениях системы. Первый индекс чисел 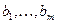 стоят в правых частях системы (индекс – номер уравнения).
стоят в правых частях системы (индекс – номер уравнения).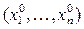 называется решением системы (6), если при подстановке этих чисел вместо неизвестных
называется решением системы (6), если при подстановке этих чисел вместо неизвестных 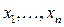 в каждое уравнение (6) получается верное числовое равенство. Система может иметь решения, а может не иметь. Если система имеет решения, то она может иметь только одно решение (т.е. только один набор
в каждое уравнение (6) получается верное числовое равенство. Система может иметь решения, а может не иметь. Если система имеет решения, то она может иметь только одно решение (т.е. только один набор 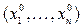 ), а может иметь более одного решения. В зависимости от описанной ситуации системы делятся на совместные и несовместные, определенные и неопределенные.
), а может иметь более одного решения. В зависимости от описанной ситуации системы делятся на совместные и несовместные, определенные и неопределенные.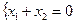 (одно уравнение с двумя неизвестными) является совместной (ее решением является, например, набор чисел (0,0)). Эта система является неопределенной, так как ее решениями, очевидно, являются
(одно уравнение с двумя неизвестными) является совместной (ее решением является, например, набор чисел (0,0)). Эта система является неопределенной, так как ее решениями, очевидно, являются 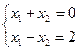 является определенной, так как имеет только одно решение (1, –1). В этом можно убедиться, решая систему «школьными» методами (выражая из одного уравнения одну неизвестную через другую и подставляя во второе уравнение).
является определенной, так как имеет только одно решение (1, –1). В этом можно убедиться, решая систему «школьными» методами (выражая из одного уравнения одну неизвестную через другую и подставляя во второе уравнение).


