
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль 3. Дифференциальное исчисление функции одной
Переменной Содержание модуля. Тема 3.1. Задачи, приводящие к понятию производной. Определение производной. Ее геометрический и механический смысл. Правила дифференцирования функций. Производные основных элементарных функций. Производная сложной и обратной функции. Производные высших порядков. Тема 3. 2. Дифференциал функции, его геометрический смысл. Инвариантность формы дифференциала. Дифференцирование функций, заданных параметрически. Применение дифференциала в приближенных вычислениях. Правило Лопиталя.Точки экстремума функции. Теорема Ферма. Теоремы Ролля, Лагранжа, Коши
Методические указания по его изучению. После изучения по учебникам теоретического материала разберите реше- ние примеров 6, 7. Для справок приведем правила и формулы дифференцирования основных элементарных функций. 1. 3. 5. Если 6. 8. 10. 12. 14. 16. 18. Если u= х, то u ′ = 1.
Пример 6. Найти производные данных функций: а) г) Решение. а) применяем правило дифференцирования сложной функции и табличные формулы:
б) Последовательно применяем правило дифференцирования сложной функции:
в) Логарифмируем данную функцию: Дифференцируем обе части последнего равенства: Отсюда
г) Данная функция задана в неявной форме. Дифференцируя по х обе части уравнения, имеем
Отсюда
д) Прологарифмируем по основанию е обе части данного равенства:
Пример 7. Найти дифференциал функции Решение.. Дифференциалом dy функции вается главная, линейная относительно ∆ х часть у ′∆ х приращения ∆ у функции, то есть Исходя из определения дифференциала, имеем:
Вопросы для самоконтроля. 1. Что называется производной функции? 2. Каков геометрический, физический смысл производной? 3. Какая функция называется дифференцируемой в точке? на интервале? 4. Как взаимосвязаны непрерывность и дифференцируемость функции в точке? 5. Напишите правила дифференцирования функций. 6. Напишите формулы дифференцирования основных элементарных функций.
7. Сформулируйте правило дифференцирования сложной функции. 8. Сформулируйте определение дифференциала функции. 9. Перечислите свойства дифференциала функции. 10. Каков геометрический смысл дифференциала функции?
2. 3. 4. Задания для самостоятельной работы В задачах 1 – 3 найти производные указанных функций. 1. 4.Найти дифференциал функции 5.Вычислить предел
Модуль 4. Применение дифференциального исчисления к исследованию функций. Содержание модуля. Тема 4. 1. Условия монотонности функций. Экстремумы функции, необходимое условие. Достаточные условия. Отыскание наибольшего и наименьшего значений функции, дифференцируемой на отрезке. Тема 4. 2.Исследование выпуклости графика функции. Точки перегиба. А симптоты графика функции. Общая схема исследования функции и построения ее графика. Уравнение касательной к кривой в данной точке.
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.227.69 (0.011 с.) |
 . 2.
. 2. 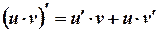 .
. . С – const. 4.
. С – const. 4.  .
.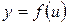 , где
, где  , то
, то  .
.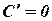 7.
7.  .
. . 9.
. 9.  .
. . 11.
. 11.  .
. . 13.
. 13.  .
.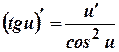 . 15.
. 15.  .
. . 17.
. 17.  .
.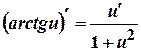 . 19.
. 19.  .
. ; б)
; б)  . в)
. в)  ;
; ; д)
; д)  .
.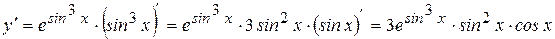 .
.

 .
. .
.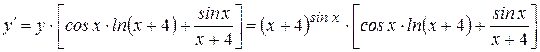 .
.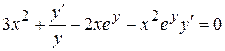 .
. ;
; 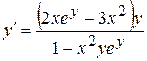 .
. . Дифференцируем обе части последнего равенства по переменной х, считая здесь у функцией от х:
. Дифференцируем обе части последнего равенства по переменной х, считая здесь у функцией от х: ,
, , откуда
, откуда .
. .
. в точке х назы-
в точке х назы- .Так как
.Так как  , то
, то 
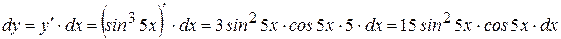 .
. . 2.
. 2.  . 3.
. 3.  .
.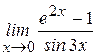 , используя правило Лопиталя.
, используя правило Лопиталя.


