Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формы представления гармонических колебаний
Графическое временное представление гармонических колебаний неудобно, т.к. при их построении необходимо вычислять величины в текущие моменты времени и по точкам их отсчета строить графики. Если несколько величин Например, величины рис. 3.4 можно записать:
и представить на рис. 3.6, для времени Рис. 3.6. Представление синусоидальных токов в виде векторов На этой фигуре, имеем:
Представление синусоидальных величин в виде рис. 3.6 получило название векторная форма. Векторные диаграммы успешно используются при анализе режимов работы цепей. Совокупность векторов ЭДС, напряжений и токов, изображенных в общей системе координат, называется векторной диаграммой, которая дает наглядное представление об амплитудах (или действующих значениях), начальных фазах Использование временной и векторной формы синусоидальных величин Для решения этой проблемы используют представление гармонических колебаний в виде комплексных чисел (векторов). Расчет электрических цепей с использованием представления гармонических колебаний (тока, напряжения, ЭДС) в виде комплексных векторов называется символическим методом. Рис. 3.7. Вектор Рис. 3.8. Вектор тока на комплексной плоскости Некоторые сведения из курса математики: Сумма вещественного и мнимого чисел называется комплексным числом. Обозначается комплексное число буквой с чертой под ней:
В основе вычислений комплексных чисел лежит формула Эйлера
где Формулы перехода между формами представления комплексного числа отражает выражение (3.5). Обратный переход осуществляют по формулам:
Комплексное число легко представляется в комплексной плоскости (рис. 3.7) Пусть задан комплексный ток, используя формулу Эйлера получим:
В выражении (3.8)
Соответственно, представляют косинусоидальную и синусоидальную формы записи гармонических колебаний (см. п. 3.1). Таким образом, косинусоидальная и синусоидальная форма записи (3.9) мгновенных величин Аналогично комплексному току Комплексный ток легко представляется в комплексной плоскости рис. 3.8. Три синусоидальныхтока (рис. 3.4), имеющих временную форму записи,
На рисунке 3.9 показаны эти три тока в виде векторов на комплексной плоскости. Рис. 3.9. Комплексные токи Преимущество комплексного представления величин: 1. Форму представления комплексного тока можно изменить:
Оператор поворота Примем в качестве комплексного тока вектор
где "≓" — знак соответствия комплексной и синусоидальной форсм представления величин. Аналогично для напряжения и ЭДС:
Величины 2. Комплексные 3. Сложение (вычитание) комплексных чисел производят 4. Умножение (деление) комплексных чисел производит в показательной форме их представления; 5. Дифференцирование (интегрирование) величин во времени равносильно умножению (делению) на оператор 6. Умножение на Пример 3.2. Дано комплексное действующие значение тока Решение. Действующее значение тока (3.6)
амплитуда тока
начальная фаза тока (3.7)
Искомое мгновенное значение тока
Угловая частота Пример 3.3. Заданы параметры синусоидального тока: амплитуда Решение.
Пример 3.4. Задано комплексное напряжение Решение. Комплексное напряжение
По известному действующему значению напряжения определим
угловая частота
мгновенное значение напряжения (3.11)
Пример 3.5. Найдем произведение двух комплексных напряжений:
При умножении комплексных чисел их модули перемножаются,
Пример 3.6. Найдем сумму двух комплексных напряжений:
Для сложения двух комплексных чисел необходимо записать каждое из них
Складывая отдельно вещественные и мнимые части
Преобразуем в показательную форму, используя (3.6) и (3.7):
Основные положения, изложенные в п. 3.2 материалов:
|
||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 291; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.88.249 (0.034 с.) |
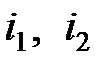 , имеют одинаковую угловую скорость
, имеют одинаковую угловую скорость 
 и начальной фазой
и начальной фазой 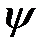 , то возможно упростить их представление.
, то возможно упростить их представление. ;
; ; (3.4)
; (3.4)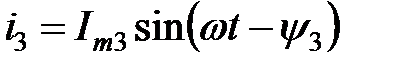 .
. в виде векторов
в виде векторов  , которые вращаются с угловой скоростью
, которые вращаются с угловой скоростью  вокруг оси
вокруг оси  .
.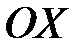 — ось координат;
— ось координат; — модули векторов, длины которых могут быть равны амплитудным
— модули векторов, длины которых могут быть равны амплитудным 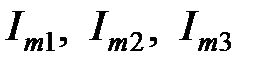 или действующим
или действующим 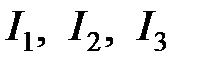 значениям токов;
значениям токов; — начальные фазы токов
— начальные фазы токов 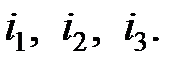
 их взаимное положение зависит не от начальных фаз, а от угла сдвига фаз между ними.
их взаимное положение зависит не от начальных фаз, а от угла сдвига фаз между ними. (рис. 3.4, рис. 3.5) проблематично.
(рис. 3.4, рис. 3.5) проблематично. на комплексной плоскости
на комплексной плоскости . Здесь
. Здесь — вещественная часть комплексного числа
— вещественная часть комплексного числа  , т.е.
, т.е. 
 — мнимая часть комплексного числа
— мнимая часть комплексного числа  , т.е.
, т.е.  .
. (3.5)
(3.5) — комплексное число,
— комплексное число,  — модуль комплексного числа,
— модуль комплексного числа,  — аргумент комплексного числа,
— аргумент комплексного числа, 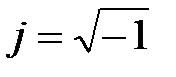 — мнимая единица (в математике её обозначают буквой
— мнимая единица (в математике её обозначают буквой  , однако в электротехнике этой буквой обозначают мгновенное значение тока); соответственно: показательная, тригонометрическая и алгебраическая формы представления комплексного числа;
, однако в электротехнике этой буквой обозначают мгновенное значение тока); соответственно: показательная, тригонометрическая и алгебраическая формы представления комплексного числа;  — обозначается в виде
— обозначается в виде — действительная часть комплексного числа;
— действительная часть комплексного числа;  — обозначается в виде
— обозначается в виде  — мнимая часть комплексного числа.
— мнимая часть комплексного числа. (3.6)
(3.6) (3.7)
(3.7) ).
).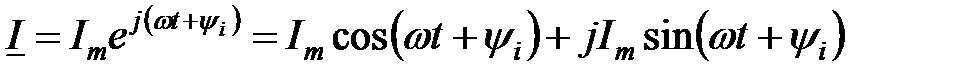 (3.8)
(3.8) , (3.9)
, (3.9)
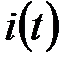 однозначно связана с (3.8) комплексным представлением тока
однозначно связана с (3.8) комплексным представлением тока  и наоборот.
и наоборот.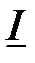 (3.8) представляют комплексное напряжение
(3.8) представляют комплексное напряжение 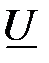 и комплексную ЭДС
и комплексную ЭДС 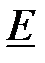 .
.


 ,
, присутствует в качестве общего множителя во всех законах электротехники Ома (2.1), (2.5), Кирхгофа (1.18), (1.19) поэтому его можно вынести за скобку правой и левой частей уравнений и сократить. Оператор поворота
присутствует в качестве общего множителя во всех законах электротехники Ома (2.1), (2.5), Кирхгофа (1.18), (1.19) поэтому его можно вынести за скобку правой и левой частей уравнений и сократить. Оператор поворота 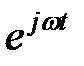 не участвует в расчетах цепей символическим методом.
не участвует в расчетах цепей символическим методом.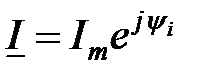 , используя понятие действующего значения тока (3.2)
, используя понятие действующего значения тока (3.2) 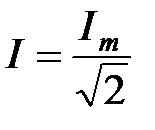 , окончательно запишем
, окончательно запишем  ≓
≓ 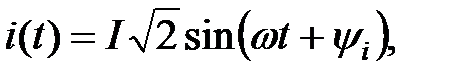 (3.10)
(3.10)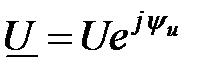 ≓
≓  (3.11)
(3.11) ≓
≓ 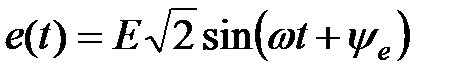 . (3.12)
. (3.12)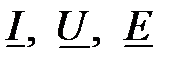 называются комплексными, соответственно, тока, напряжения и ЭДС;
называются комплексными, соответственно, тока, напряжения и ЭДС; легко изображаются в комплексной плоскости (рис. 3.8, рис. 3.9)
легко изображаются в комплексной плоскости (рис. 3.8, рис. 3.9) их комплексного представления;
их комплексного представления; равносильно повороту комплексного вектора
равносильно повороту комплексного вектора .
. .
.  A;
A; A;
A; .
. A.
A. предполагается известной.
предполагается известной. А, начальная фаза
А, начальная фаза 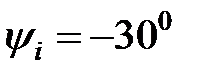 , угловая частота
, угловая частота 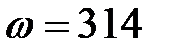 рад/с. Требуется записать мгновенное значение тока, рассчитать его комплексное действующие значение
рад/с. Требуется записать мгновенное значение тока, рассчитать его комплексное действующие значение  A;
A;  A;
A; A.
A.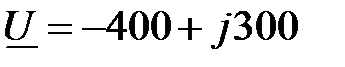 ; частота
; частота Гц. Требуется найти мгновенное значение напряжения
Гц. Требуется найти мгновенное значение напряжения  .
. из алгебраической формы переведем
из алгебраической формы переведем  B;
B; ;
;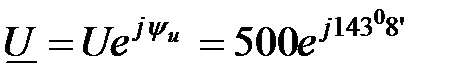 B.
B.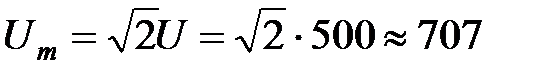 B;
B; рад/с;
рад/с;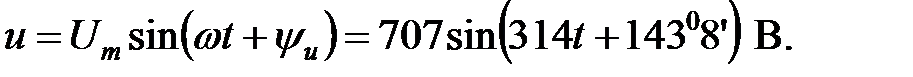


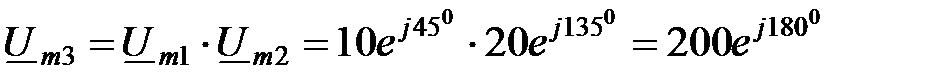 .
. В и
В и 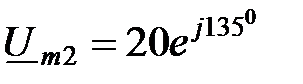 В.
В.

 и
и 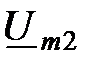 , получаем
, получаем