Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывность в точке. Виды разрывов.
Определение. Функция В определении предела функции при Определение. Пусть функция Определение. Пусть функция Определение. Функция 1) функция 2) существует предел значений функции слева: 3) существует предел значений функции справа: 4) эти два предела совпадают между собой и со значением функции в точке
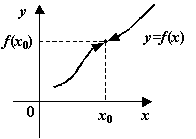
Рис.14.1.Функция непрерывна: пределы слева и справа совпадают с Пример 14.1. Пусть Дадим теперь определение точек разрыва функции. Определение. Точка 1) не существует предела слева 2) не существует предела справа 3) пределы слева 4) пределы слева Если имеет место либо случай 3, либо случай 4, то точка разрыва
Если же имеет место либо случай 1, либо случай 2 (либо и тот и другой сразу), то точка разрыва Итак, если функция
Рис.14.2. Если значения на берегах разрыва разные, то значение функции в точке
Рис.14.3. Наконец, к разрывам второго рода, как видно из определения, относятся все разрывы, которые не принадлежат к разрывам первого рода; некоторые из возможных способов поведения функции в окрестности точки
Рис.14.4. Пример 14.2. Рассмотрим функцию
В точках (значения на краях разрыва существуют, но не совпадают); в точке (снова пределы слева и справа существуют, но не совпадают).
Рис.14.5. График функции Пример 14.3. Функция
Рис.14.6. График функции Пример 14.4. Возьмём
Рис.14.7. Устранимый разрыв функции Замечание. Если функция Пример 14.5. Рассмотрим функцию
Рис.14.8. График функции
|
||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 406; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.55.14 (0.016 с.) |
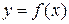 называется непрерывной в точке
называется непрерывной в точке 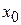 , если существует предел функции в этой точке и он равен значению функции в этой точке, т. е.
, если существует предел функции в этой точке и он равен значению функции в этой точке, т. е.  .
. считается, что
считается, что  стремится к
стремится к  определена на некотором полуинтервале
определена на некотором полуинтервале 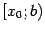 , для которого
, для которого  - левый конец. Функция
- левый конец. Функция  и этот предел равен значению
и этот предел равен значению  , то есть
, то есть 
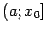 , для которого
, для которого 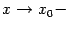 и этот предел равен значению
и этот предел равен значению 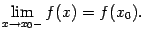
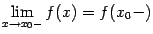 ;
;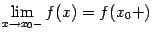 ;
; .
.
 и
и  . Тогда
. Тогда  и
и  . Эти значения совпадают, значит, функция
. Эти значения совпадают, значит, функция 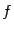 непрерывна в точке
непрерывна в точке 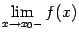 ;
; ;
;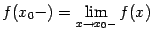 и справа
и справа  существуют, но не равны друг другу:
существуют, но не равны друг другу: 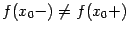 ;
;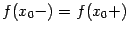 , но не совпадают со значением функции в точке
, но не совпадают со значением функции в точке 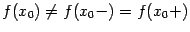 , или функция не определена в точке
, или функция не определена в точке 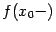 и
и 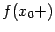 , но точка
, но точка 
 , то полученная изменённая функция будет уже непрерывна в точке
, то полученная изменённая функция будет уже непрерывна в точке 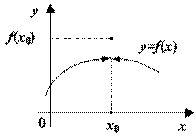



 , для которой
, для которой Функция имеет разрывы при
Функция имеет разрывы при  и при
и при 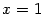 . Нетрудно видеть, что при
. Нетрудно видеть, что при 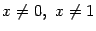
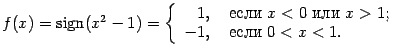




 имеет при
имеет при  при
при 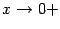 и
и 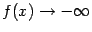 при
при  .
.
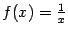
 . Все точки области определения
. Все точки области определения  этой элементарной функции являются точками непрерывности. Поскольку
этой элементарной функции являются точками непрерывности. Поскольку 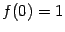 , то функция становится непрерывной в точке 0. Значит, 0 - точка разрыва первого рода для функции
, то функция становится непрерывной в точке 0. Значит, 0 - точка разрыва первого рода для функции 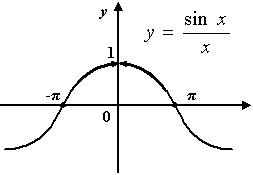

 . Её область определения -
. Её область определения -  . При
. При  и при
и при 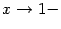 знаменатель
знаменатель  стремится к 0 и положителен, так что
стремится к 0 и положителен, так что  и
и 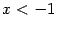 и при
и при 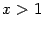 .
.