
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные операторы и матрицы. Собственные векторы линейных операторов.
Одно из фундаментальных понятий матричной алгебры — понятие линейного оператора. Рассмотрим два линейных пространства: Определение. Если задан закон (правило), по которому каждому вектору x пространства Определение.Оператор (преобразование) называют линейным, если для любых векторов х и y пространства 1. Ã(x+y) = Ã(x) + Ã(y) -свойство адаптивности оператора; 2. Ã(ʎх) = ʎÃ(х) — свойство однородности оператора. Вектор y= Ã(х) называется образом вектора х, а сам вектор х - прообразом вектора y. Если пространства Выберем в пространстве
В силу линейности оператора Ã получаем
Поскольку Пусть Тогда
С другой стороны вектор y=Ã(х), имеющий в том же базисе
Ввиду единственности разложения вектора по базису равны правые части равенства, откуда:
Определение. Матрица Таким образом, каждому линейному оператору соответствует матрица в данном базисе. Справедливо и обратное: всякой матрице т-ого порядка соответствует линейный оператор т-мерного пространства. Связь между вектором х и его образом y=Ã(х) можно выразить в матричной форме уравнением Y=AX, где А — матрица линейного оператора, Определение: Вектор Число ʎ называется собственным значением оператора Ã (матрицы А),соответствующим вектору х. Из определения следует, что собственный вектор под действием линейного оператора А переходит в вектор, коллинеарный самому себе, т.е. просто умножается на некоторое число. В то же время несобственные векторы преобразуются более сложным образом. В связи с этим понятие собственного вектора является очень полезным и удобным при изучении многих вопросов матричной алгебры и ее приложений.
Равенство (6.2) можно записать в матричной форме: АХ= ʎХ (6.3) где Х — матрица-столбец из координат вектора х. Или в развернутом виде
Квадратичные формы.
Определение. О днородный многочлен второй степени относительно переменных х1 и х2 Ф(х1, х2) = а 11 не содержащий свободного члена и неизвестных в первой степени, называется квадратичной формой переменных х1 и х2. Определение. Однородный многочлен второй степени относительно переменных х1, х2 и х3
не содержащий свободного члена и неизвестных в первой степени называется квадратичной формой переменных х1, х2 и х3.
Рассмотрим квадратичную форму двух переменных. Квадратичная форма имеет симметрическую матрицу А =
Пусть на плоскости задан ортогональный базис Если задана квадратичная форма Ф(х1, х2) = а 11
8. Кривые второго порядка на плоскости (окружность, эллипс, гипербола, парабола).
Определение. Кривой второго порядка называется множество точек, координаты которых удовлетворяют уравнению второго порядка
где Определение. Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружности. Получим уравнение окружности, если известны ее центр и радиус. Окружность радиуса
Определение. Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, назывемых фокусами эллипса, есть величина постоянная. Пусть
Пусть сумма расстояний от точки эллипса до фокусов равна где
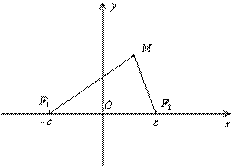
Рис.8.2. Уравнение (8.2) называется каноническим уравнением эллипса. Определение. Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная. Для получения уравнения гиперболы выберем систему координат. Начало координат расположим на середине отрезка между фокусами, ось
Рис. 8.3. Пусть расстояние между фокусами где Уравнение (8.3) называется каноническим уравнением гиперболы. Определение. Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой, параболы. Чтобы получить уравнение кривой, соответствующей этому определению, введем подходящую систему координат. Для этого из фокуса
Рис. 8.4. Пусть расстояние между фокусом
Уравнение (8.4) называется каноническим уравнением параболы.
|
||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 580; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.1.232 (0.02 с.) |
 размерности n и
размерности n и  размерности m.
размерности m. и
и  совпадают, то оператор А отображает пространство
совпадают, то оператор А отображает пространство  . Запишем разложение произвольного вектора х по данному базису:
. Запишем разложение произвольного вектора х по данному базису:

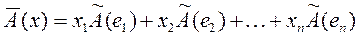
 (l= 1,2,...,n) — также вектор из
(l= 1,2,...,n) — также вектор из 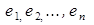 .
. (i = 1,2,…,n) (6.1)
(i = 1,2,…,n) (6.1)

 координаты
координаты  можно записать так:
можно записать так:
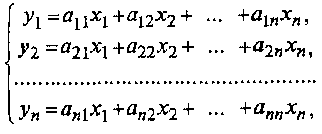
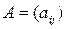 (i,j =1,2,...,n) называется матрицей оператора Ã в базисе
(i,j =1,2,...,n) называется матрицей оператора Ã в базисе  ,
,  -матрицы-столбцы из координат векторов х и y.
-матрицы-столбцы из координат векторов х и y. ,называется собственным вектором линейного оператора Ā, если найдется такое число ʎ,что Ã(х)= ʎх (6.2)
,называется собственным вектором линейного оператора Ā, если найдется такое число ʎ,что Ã(х)= ʎх (6.2)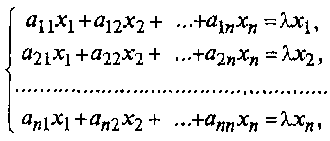
 ,
,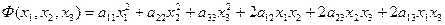
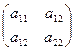 . Определитель этой матрицы называется определителем квадратичной формы.
. Определитель этой матрицы называется определителем квадратичной формы. . Каждая точка плоскости имеет в этом базисе координаты х1, х2.
. Каждая точка плоскости имеет в этом базисе координаты х1, х2.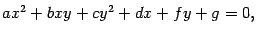
 - вещественные числа, и хотя бы одно из чисел
- вещественные числа, и хотя бы одно из чисел  отлично от нуля.
отлично от нуля.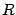 с центром в точке
с центром в точке  имеет уравнение:
имеет уравнение: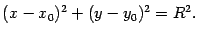 (8.1.)
(8.1.)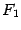 и
и 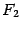 - фокусы эллипса. Начало
- фокусы эллипса. Начало 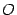 системы координат расположим на середине отрезка
системы координат расположим на середине отрезка 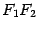 . Ось
. Ось 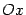 направим вдоль этого отрезка, ось
направим вдоль этого отрезка, ось 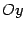 - перпендикулярно к этому отрезку (рис. 8.2).
- перпендикулярно к этому отрезку (рис. 8.2).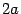 , а расстояние между фокусами -
, а расстояние между фокусами - 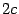 . Тогда в выбранной системе координат эллипс имеет уравнение:
. Тогда в выбранной системе координат эллипс имеет уравнение: 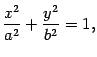 (8.2)
(8.2)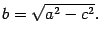
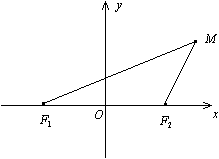
 (8.3)
(8.3)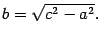
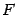 опустим перпендикуляр
опустим перпендикуляр 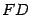 на директрису
на директрису  . Начало координат
. Начало координат  . Ось
. Ось 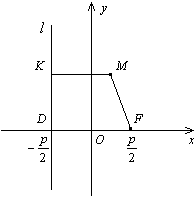
 . Тогда в выбранной системе координат парабола имеет уравнение
. Тогда в выбранной системе координат парабола имеет уравнение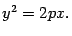 (8.4)
(8.4)


