
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Реальное дифференцирующее звено
Такое звено является последовательным соединением дифференцирующего и инерционного звеньев, его передаточная функция имеет вид
ЛАЧХ и ЛФЧХ складываются, т.е.
На рис. 3.8, а приведены логарифмические частотные характеристики реального дифференцирующего звена. До частоты сопряжения Расчетное выражение для переходной функции этого звена может быть получено по формуле (2.14) при
На рис. 3.8, б приведена переходная характеристика звена. Она спадает по экспоненте до нуля от значения
Передаточная функция
где
Рис. 3.8 — ЛАЧХ и ЛФЧХ (а), переходная характеристика (б) реального дифференцирующего звена и его реализация на операционном усилителе (в)
Звенья второго порядка
В общем случае звено второго порядка описывается уравнением
или в операторной форме записи
Отсюда определяем передаточную функцию:
В зависимости от характера полюсов передаточной функции (3.1) (корней уравнения
Апериодическое звено второго порядка
Это звено имеет место при отрицательных вещественных полюсах передаточной функции (3.1), которую в этом случае можно представить в виде:
где эквивалентные постоянные времени
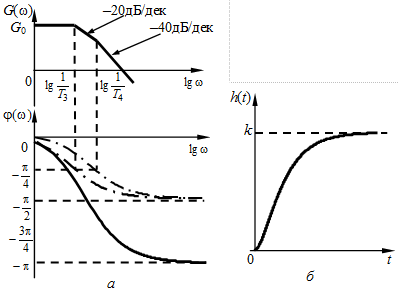
Анализируя выражение передаточной функции (3.2), можно сделать вывод о том, что апериодическое звено второго порядка состоит из двух инерционных (апериодических) звеньев с эквивалентными постоянными времени На рис. 3.9, а показаны ЛАЧХ и ЛФЧХ апериодического звена второго порядка. До частоты сопряжения
Рис. 3.9 — ЛАЧХ и ЛФЧХ (а), переходная характеристика (б)
апериодического звена второго порядка
По формуле (2.14) получим расчетное выражение для переходной функции апериодического звена второго порядка. Для него
Переходная характеристика звена показана на рис. 3.9, б, ее характерная особенность — наличие точки перегиба вследствие суммирования двух экспоненциальных составляющих.
Колебательное звено
Это звено получается при комплексных сопряженных полюсах передаточной функции (3.1). Передаточную функцию звена удобнее записывать в виде
где Получим формулы для частотных характеристик колебательного звена:
Частотные характеристики колебательного звена приведены на рис. 3.10. Они существенно зависят от величины коэффициента демпфирования
Рис. 3.10 — Частотные характеристики колебательного звена
Величина «горба» на частоте
Переходная функция колебательного звена может быть получена по формуле (2.14) при комплексных сопряженных полюсах
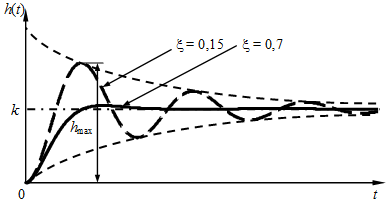
На рис. 3.11 показаны переходные характеристики колебательного звена, рассчитанные по выражению (3.4) для различных значений коэффициента демпфирования
Примером звена второго порядка может служить колебательный контур (см. схему на рис. 2.6 и вывод передаточной функции в примере 2.5).
Рис. 3.11 — Переходные характеристики колебательного звена
Пример 3.2 Определить, при каком соотношении параметров элементов схемы колебательный контур (см. рис. 2.6) является колебательным звеном. Запишем полученную в примере 2.5 передаточную функцию с использованием коэффициента демпфирования:
Отсюда выразим коэффициент демпфирования:
Звено будет колебательным, если
В противном случае, т.е. при
контур будет являться апериодическим звеном второго порядка. Следует обратить внимание на то, что лишь с позиций математического описания схему можно представить как последовательное соединение двух апериодических звеньев первого порядка. Расчленить же принципиальную схему на два участка, каждый из которых был бы соответствующим апериодическим звеном первого порядка, невозможно. Пример 3.3 Вывести передаточную функцию и определить ее параметры для устройства, схема которого приведена на рис. 3.12, а. Устройство выполнено на операционных усилителях, реализующих инерционное, интегрирующее и пропорциональное звенья (см. разделы 3.2.1.1, 3.2.1.2, 3.2.1.4). На выходе усилителя DA 1 происходит преобразование и суммирование напряжений по каждому из его входов. Его передаточные функции относительно входного напряжения
Полученный сигнал проходит через последовательно включенное интегрирующее звено на усилителе DA 2 с передаточной функцией Выход усилителя DA 2 образует выход устройства и сигнал с него через усилитель DA 3 с передаточной функцией
Рис. 3.12 — Устройство на операционных усилителях (а) и его структурная схема (б)
На рис. 3.12, б приведена структурная схема, соответствующая устройству, изображенному на рис. 3.12, а. Эквивалентная передаточная функция участка схемы, охваченного обратной связью, рассчитывается по выражению:
Таким образом, передаточная функция устройства, изображенного на рис. 3.12, а, будет равна
где Рассмотренное устройство позволяет легко реализовать как колебательное, так и апериодическое звено второго порядка. Если, например, принять
Консервативное звено
Это звено получается при мнимых полюсах передаточной функции (3.1), и его можно рассматривать как частный случай колебательного звена при
На рис. 3.13, а изображены логарифмические частотные характеристики консервативного звена. Точная ЛАЧХ (сплошная линия) терпит разрыв непрерывности второго рода на частоте сопряжения
консервативного звена Переходная функция консервативного звена может быть получена по формуле (2.10) при мнимых полюсах
На рис 3.13, б показана переходная характеристика консервативного звена, она представляет собой незатухающие автоколебания частотой Консервативное звено на пассивных четырехполюсниках не реализуется. Если обратиться к приведенному выше примеру (см. рис. 2.6), то должны отсутствовать потери в контуре, т.е. выполняться условие
Особые звенья линейных САУ Неминимально-фазовые звенья
В ряде устройств, например при мостовых соединениях, процессы описываются дифференциальным уравнением, имеющим отрицательные коэффициенты в правой части:
Передаточная функция такого звена будет иметь вид
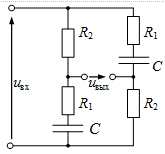
т.е. имеет положительный нуль Такие звенья относятся к устойчивым неминимально-фазовым звеньям первого порядка, их характеристики похожи на характеристики инерционного форсирующего звена. Пример 3.5 На рис. 3.14 приведена мостовая схема, в которой выполняется соотношение
т.е. где
Рис. 3.14 — Пример неминимально- фазового устойчивого звена
На рис. 3.15, а показаны логарифмические частотные характеристики этого звена при
Рис. 3.15 — Характеристики устойчивого неминимально-фазового звена
Неустойчивые неминимально-фазовые звенья содержат в передаточных функциях положительные полюсы. Примером такого звена может служить асинхронный двигатель, работающий в режиме максимального скольжения. Другой пример — охват минимально-фазового звена положительной обратной связью. Пусть инерционное звено с передаточной функцией
где
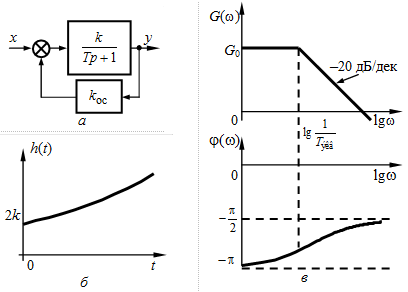
Рис. 3.16 — Неустойчивое неминимально-фазовое звено (а) и его характеристики (б, в)
При
На рис. 3.16, б приведена переходная характеристика этого звена, она неограниченно нарастает, начиная со значения Звено чистого запаздывания
Это звено относится к трансцендентным, его передаточная функция имеет вид:
Получим расчетные формулы для частотных характеристик звена:
Рис. 3.17 — Частотные (а, б) и временные (в, г) характеристики звена чистого запаздывания Годограф АФЧХ (рис. 3.17, а) представляет собой окружность радиуса Звено чистого запаздывания без искажения воспроизводит на выходе входную величину, как идеальное пропорциональное звено, но с той разницей, что выходная величина запаздывает относительно входной на постоянное время
Устойчивость САУ
|
||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 1478; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.174.95 (0.07 с.) |
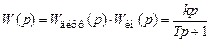 .
.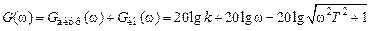 ,
,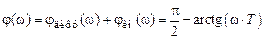 .
.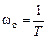 ЛАЧХ проходит с наклоном +20 дБ/дек, а после нее — горизонтально. Суммарная ЛФЧХ представляет собой ЛФЧХ инерционного звена, смещенную за счет дифференцирующего звена на угол
ЛАЧХ проходит с наклоном +20 дБ/дек, а после нее — горизонтально. Суммарная ЛФЧХ представляет собой ЛФЧХ инерционного звена, смещенную за счет дифференцирующего звена на угол 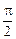 .
. ,
,  ,
, 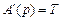 ,
, 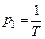 :
: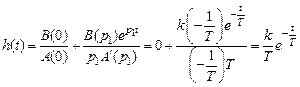 .
.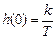 . На рис. 3.8, в приведена реализация реального дифференцирующего звена на операционном усилителе. Для такой схемы
. На рис. 3.8, в приведена реализация реального дифференцирующего звена на операционном усилителе. Для такой схемы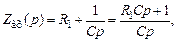
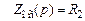 .
.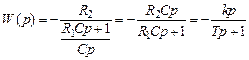 ,
,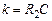 ,
, 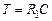 .
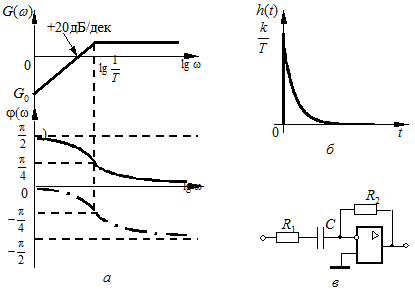
.
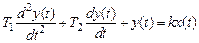 ,
,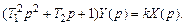
 (3.1)
(3.1)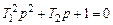 ) различают апериодическое звено второго порядка, колебательное и консервативное звенья.
) различают апериодическое звено второго порядка, колебательное и консервативное звенья.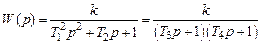 , (3.2)
, (3.2) рассчитываются по соотношению
рассчитываются по соотношению . (3.3)
. (3.3) ЛАЧХ горизонтальна на уровне
ЛАЧХ горизонтальна на уровне 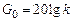 , после этой частоты до частоты сопряжения
, после этой частоты до частоты сопряжения 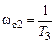 имеет наклон –20 дБ/дек, а после
имеет наклон –20 дБ/дек, а после 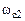 проходит с наклоном –40 дБ/дек. ЛФЧХ асимптотически приближается к значению
проходит с наклоном –40 дБ/дек. ЛФЧХ асимптотически приближается к значению 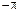 .
.
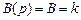 ,
, 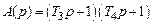 ,
, 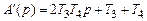 ,
, 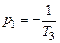 ,
, 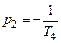 , тогда
, тогда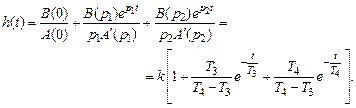
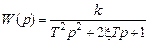 ,
, , а параметр
, а параметр 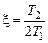 называется коэффициентом демпфирования. Для колебательного звена
называется коэффициентом демпфирования. Для колебательного звена 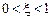 . Можно также отметить, что при
. Можно также отметить, что при  полюсы передаточной функции (3.1) становятся вещественными и звено будет апериодическим второго порядка.
полюсы передаточной функции (3.1) становятся вещественными и звено будет апериодическим второго порядка.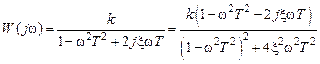 ,
,
 ,
,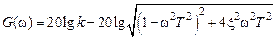 ,
,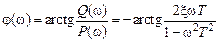 .
.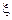 . При
. При  АЧХ
АЧХ 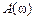 (рис. 3.10, а) монотонно уменьшается с увеличением частоты. При
(рис. 3.10, а) монотонно уменьшается с увеличением частоты. При 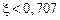 на ней появляется «горб», который увеличивается по мере уменьшения
на ней появляется «горб», который увеличивается по мере уменьшения 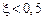 , при больших значениях коэффициента демпфирования ЛАЧХ приближается к ее асимптотическому варианту (имеет нулевой наклон до частоты сопряжения
, при больших значениях коэффициента демпфирования ЛАЧХ приближается к ее асимптотическому варианту (имеет нулевой наклон до частоты сопряжения 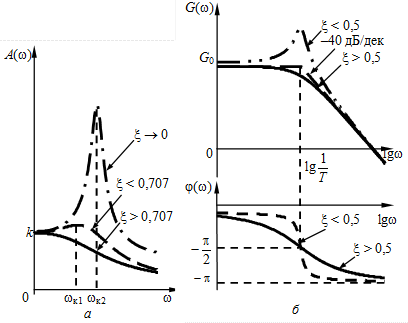
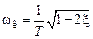 может быть оценена по соотношению [6]:
может быть оценена по соотношению [6]: .
.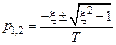 (при
(при  выражение
выражение 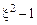 становится меньше нуля):
становится меньше нуля):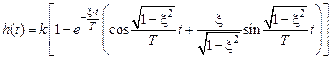 . (3.4)
. (3.4)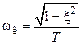 и равна мнимой части полюсов
и равна мнимой части полюсов 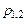 . Ее можно также определить и по АЧХ (см. рис. 3.10, а, частоты
. Ее можно также определить и по АЧХ (см. рис. 3.10, а, частоты 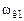 и
и 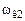 , соответствующие максимальным значениям на АЧХ). Огибающая (см. пунктир на рис. 3.11) определяется формулой
, соответствующие максимальным значениям на АЧХ). Огибающая (см. пунктир на рис. 3.11) определяется формулой 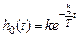 . Время переходного процесса на практике оценивается соотношением
. Время переходного процесса на практике оценивается соотношением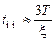 .
.


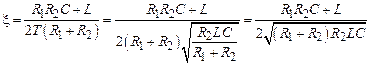 .
.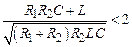 .
.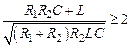 ,
,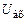 и напряжения обратной связи
и напряжения обратной связи 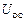 представляются выражениями
представляются выражениями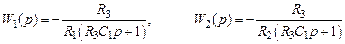 .
.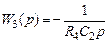 .
.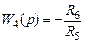 поступает на второй вход усилителя DA 1.
поступает на второй вход усилителя DA 1.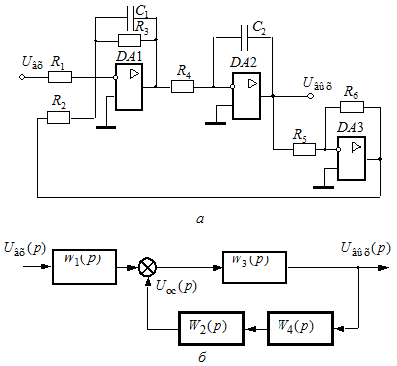

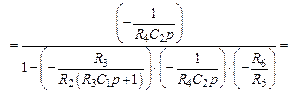
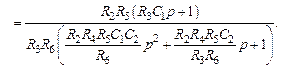
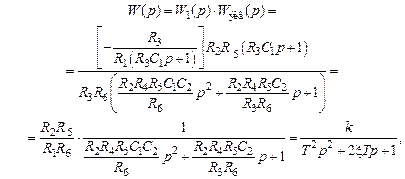
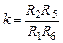 ,
, 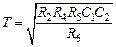 ,
, 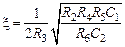 .
. , то при известных значениях
, то при известных значениях 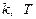 и
и 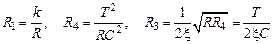 . (3.5)
. (3.5) . Выражения для передаточной и некоторых частотных функций звена будут иметь вид:
. Выражения для передаточной и некоторых частотных функций звена будут иметь вид: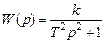 ,
,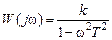 ,
, 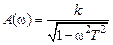 ,
,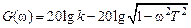 .
.
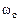 терпит разрыв непрерывности первого рода (фаза скачком изменяется от 0 до
терпит разрыв непрерывности первого рода (фаза скачком изменяется от 0 до 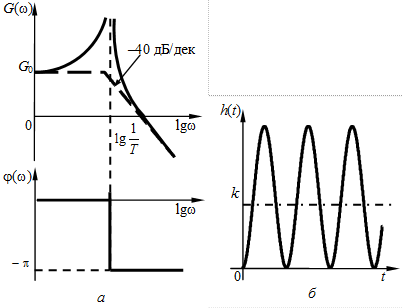 Рис. 3.13 — ЛАЧХ, ЛФЧХ (а), переходная характеристика (б)
Рис. 3.13 — ЛАЧХ, ЛФЧХ (а), переходная характеристика (б)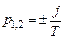 и имеет вид
и имеет вид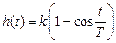 .
.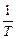 и амплитудой
и амплитудой 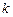 .
.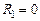 , что физически невозможно. В устройстве, схема которого приведена на рис. 3.12, а, в соответствии с формулами (3.5) получение консервативного звена возможно при
, что физически невозможно. В устройстве, схема которого приведена на рис. 3.12, а, в соответствии с формулами (3.5) получение консервативного звена возможно при  . Для этого резистор
. Для этого резистор 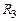 просто нужно удалить из устройства.
просто нужно удалить из устройства. .
.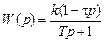 ,
, .
.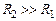 . Для нее будет иметь место соотношение:
. Для нее будет иметь место соотношение: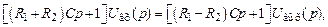
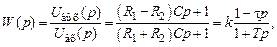
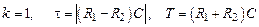 .
.
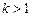 . Его ЛАЧХ не отличается от ЛАЧХ инерционного форсирующего звена при
. Его ЛАЧХ не отличается от ЛАЧХ инерционного форсирующего звена при 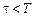 , а ЛФЧХ изменяется в диапазоне
, а ЛФЧХ изменяется в диапазоне 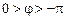 . Переходная характеристика (рис. 3.15, б) имеет при
. Переходная характеристика (рис. 3.15, б) имеет при 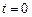 скачок в отрицательном направлении.
скачок в отрицательном направлении.
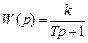 охвачено положительной обратной связью с коэффициентом передачи
охвачено положительной обратной связью с коэффициентом передачи 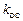 (рис. 3.16, а). Передаточная функция получившегося эквивалентного звена будет иметь вид:
(рис. 3.16, а). Передаточная функция получившегося эквивалентного звена будет иметь вид:
 .
.
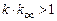 величины
величины 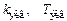 становятся отрицательными и передаточная функция
становятся отрицательными и передаточная функция 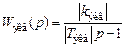 становится такой, что ее полюс
становится такой, что ее полюс 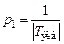 будет положительным.
будет положительным.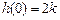 , поскольку рассчитывается по формуле
, поскольку рассчитывается по формуле  . ЛАЧХ неустойчивого неминимально-фазового звена такая же, как и у инерционного звена, а ЛФЧХ, рассчитываемая по выражению
. ЛАЧХ неустойчивого неминимально-фазового звена такая же, как и у инерционного звена, а ЛФЧХ, рассчитываемая по выражению 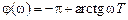 , возрастает со значения
, возрастает со значения 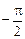 (см. рис. 3.16, в).
(см. рис. 3.16, в).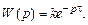
 ,
, ,
,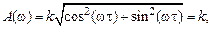
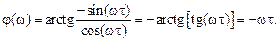
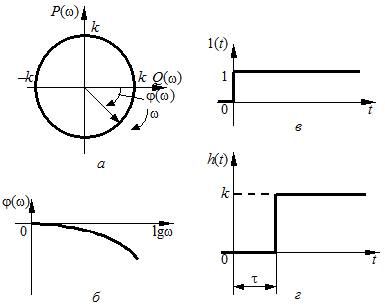
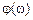 линейно убывает с ростом частоты, а ЛФЧХ (рис. 3.17, б) криволинейна за счет логарифмического масштаба по оси
линейно убывает с ростом частоты, а ЛФЧХ (рис. 3.17, б) криволинейна за счет логарифмического масштаба по оси 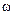 .
. (см. рис. 3.17, в, г). Переходная функция такого звена имеет вид:
(см. рис. 3.17, в, г). Переходная функция такого звена имеет вид: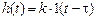 .
.


