
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Процессы скользящего среднего
Пусть ε1, ε2,..., εn,... — независимые одинаково распределенные случайные величины (белый шум). Определение. Процессом скользящего среднего (первого порядка) со средним μ (сокращенно MA(1)) называют процесс X(t):
где θ — некоторый числовой коэффициент, а μ — константа. У процесса скользящего среднего статистически зависимыми оказываются только соседние величины X(t−1) и X(t). Значения процесса, разделенные промежутком времени 2 и более, статистически независимы, ибо в их формировании участвуют разные слагаемые εt. По этой причине процессы скользящего среднего являются непосредственными простейшим обобщением процессов белого шума. Процессы авторегрессии Определение. Процессом авторегрессии (первого порядка) со средним значением μ (сокращенно AR(1)) называют случайный процесс X(t), удовлетворяющий соотношению: X(t) − μ = φ · (X(t − 1) − μ) + εt, где φ и μ — некоторые числа. Марковское свойство. Поведение многих процессов в будущем определяется только их состоянием в настоящем и воздействиями на процесс, которые будут оказываться в будущем. Определение. Случайная последовательность X(t), t ∈ T называется марковской, если для любых A, B и t P(AB|X(t)) = P(A|X(t))P(B|X(t)) Стационарность. Определение. Случайный процесс X(t) называется стационарным, если для любых n, t1, t2,..., tn и τ распределения случайных величин (X(t1),...,X(tn)) и (X(t1 + τ),...,X(tn + τ)) одинаковы. Это означает, что функции конечномерных распределений не меняются при сдвиге времени, т.е.
В частности, образующие стационарную случайную последовательность случайные величины X(1),X(2),...,X(t),... распределены одинаково (но независимыми они не являются). Этот вид стационарности называют также стационарностью в узком смысле. Числовые характеристики временных рядов: математическое ожидание, ковариационная функция, корреляционная функция, автокорреляционная функция. Стационарные процессы в широком смысле. Математическое ожидание (первый момент) случайного процесса X(t) — это функция m(t), такая, что для каждого t значение функции m(t) является математическим ожиданием случайной величины X(t):
Ковариационная функция случайного процесса X(t) (кратко cov(X(t), X(s)) — это величина B(s, t) = cov(X(t), X(s)) = M[(X(t) −m(t))(X(s) −m(s))].
Она является функцией пары переменных (t, s). Значение ковариационной функции при t = s задает дисперсию случайного процесса DX(t) = cov(X(t),X(t)). Квадратный корень из cov(X(t), X(t)) называют стандартным отклонением σ(t) случайного процесса X(t):
Корреляционная функция случайного процесса X(t) — это величина:
Из определения cov(X(t), X(s)) и corr(X(t), X(s)) следует их симметрия относительно t и s:
Автокорреляционная функция. Автокорреляционной функцией стационарного процесса X(t) называют функцию r(k) = corr(X(t), X(t + k)), где k > 0 — целое число. Величину k часто называют задержкой, или лагом. Она указывает расстояние между членами временного ряда, для которых вычисляется коэффициент корреляции. Определение. Случайный процесс X(t) называется стационарным в широком смысле, если его среднее значение m(t) постоянно, а ковариационная функция B(s, t) зависит только от расстояния между аргументами, т.е. от |t − s|. Белый шум в широком смысле. Аналогичное определение можно дать для белого шума: Определение. Временной ряд (случайный процесс) X(t) называют белым шумом (в широком смысле), если для любого t выполняется MX(t) = 0 и
Из этого определения видно, что этот белый шум является стационарным (в широком смысле) случайным процессом. На практике различие между двумя видами белого шума (в широком и в узком смысле) не всегда проводятся четко. В тех случаях, когда m(t) удается тем или другим способом оценить, преобразование Y (t) = X(t) − m(t) превращает процесс в стационарный. Выборочная АКФ. Методика получения оценок значений автокорреляционной функции r(k) во многом напоминает случай двух выборок. Разберем ее устройство на оценке r(k) — корреляции между соседними членами временного ряда Xt и Xt+1. (Напомним, что большие буквы X мы используем для обозначения случайного процесса, а малые буквы x — для обозначения реализации этого случайного процесса.) Образуем из временного ряда x1, x2,..., xn совокупность из n − 1 пар: (x1, x2), (x2, x3),..., (xn−1, xn). Первый элемент каждой пары, в силу стационарности, мы можем рассматривать как реализацию случайной величины Xt, а второй — как реализацию случайной величины Xt+1. Тогда, согласно оценка коэффициента корреляции между Xt и Xt+1 может быть записана в виде:
где
соответственно оценки средних значений величин Xt и Xt+1/ При больших значениях n, учитывая что x(1) ≈ x(2)≈ x и n/(n−1) ≈ 1, это выражение часто заменяют гораздо более простым:
Аналогичнымобразом может быть определена оценка корреляции между Xt и Xt+k или k-го члена автокорреляционной функции rk:
Точность приближения заметно снижается с ростом шага k, как в силу ухудшения точности использованных выше замен, так и в силу уменьшения числа наблюдений используемых для вычисления оценки rk Поэтому на практике обычно ограничиваются изучением небольшого числа первых членов автокорреляционной функции. Вряд ли имеет смысл рассматривать оценки rk при k > n/4. Функцию rk аргумента k при k = 1, 2,... называют выборочной автокорреляционной функцией или, если не возникает недоразумений, просто автокорреляционной функцией. (При k = 0 rk по определению равно 1 и это значение обычно исключают из рассмотрения как не несущее никакой информации.) В англоязычной литературе эту функцию также называют сериальной корреляцией. График выборочной автокорреляционной функции называют коррелограммой.
На этом графике кроме значений самой функции, обычно указывают доверительные пределы этой функции в предположении, что значения автокорреляционной функции равны 0 для всех k = 0. Свойства. Изучение свойств выборочных оценок автокорреляционной функции временного ряда — в общем случае довольно сложная и до конца не решенная задача. Например выражение дисперсии оценки rk для гауссовского процесса:
Этот результат показывает, что мы не можем оценить по конечному отрезку временного ряда дисперсию оценки rk, так как она зависит от бесконечного неизвестного числа автокорреляций rt. Поэтому на практике приходится довольствоваться лишь приближениями для данного выражения. Другая проблема изучения свойств совокупности оценок rk связана с тем, что оценки с различным шагом k коррелированы между собой. Это заметно затрудняет интерпретацию коррелограммы. Рассмотрим свойства оценок автокорреляций для временного ряда, являющегося стационарной последовательностью независимых нормально распределенных случайных величин или, другими словами, гауссовским белым шумом. В этом случае для любых k, неравных нулю, по определению rk = 0. Таким образом, все слагаемые, стоящие под знаком суммы в выражении Drk, равны нулю, кроме r20 = 1. Отсюда дисперсия rk равна:
Обратим внимание на то, что оценка rk в такой форме является смещенной. Можно показать, что Другим важным свойством оценки rk является ее асимптотическая нормальность при n →∞. Такимобразом, для каждого отдельного значения rk мы можем указать приблизительный 95% доверительный интервал в виде: Они в определенной мере позволяют судить о том, насколько изучаемый процесс напоминает белый шум. Указание 95% доверительных границ для каждого коэффициента автокорреляционной функции в отдельности не означает, что с 95% вероятностью все рассматриваемые оценки rk одновременно попадают в доверительную трубку.
|
|||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 675; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.161.116 (0.012 с.) |

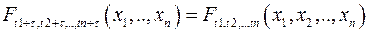

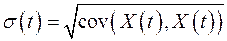










 , однако величина этого смещения стремится к нулю с ростом объема изучаемого ряда и не столь существенна в прикладном анализе.
, однако величина этого смещения стремится к нулю с ростом объема изучаемого ряда и не столь существенна в прикладном анализе. . Границы этого доверительного интервала обычно наносятся на график коррелограммы и называются доверительной трубкой.
. Границы этого доверительного интервала обычно наносятся на график коррелограммы и называются доверительной трубкой.


