
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непараметрическая линейная регрессия.
Линейный регрессионный анализ объединяет широкий круг задач, связанных с построением функциональных зависимостей между двумя группами числовых переменных: x1,..., xp и y1,..., yq. Для краткости мы объединим x1,..., xp в многомерную переменную x, а y1,..., yq —в переменную y, и будем говорить об исследовании зависимости между x и y. При этом мы будем считать x независимой переменной, влияющей на значения y. В связи с этим мы будем называть y откликом, а x = (x1,..., xp) — факторами, влияющими на отклик. Самый простой случай регрессионных задач — это исследование связи между одной независимой (одномерной) переменной x и одной зависимой переменной (откликом) y. Эта задача носит название простой регрессии. Исходными данными этой задачи являются два набора наблюдений x1, x2,..., xn — значения x и y1, y2,..., yn — соответствующие значения y. Для того, чтобы задача о подборе функции отклика f была осмысленной, мы должны определить набор допустимых функций f(x). Как правило, предполагают, что множество допустимых функций является параметрическим семейством f(x, θ), где θ ∈ Θ — параметр семейства. Тогда: yi = f(xi, θ) + εi, i= 1,..., n, (8.3) и восстановление зависимости между x и y оказывается эквивалентным указанию значения θ (точнее, ее оценки ˆθ) по исходным данным (xi, yi), i = 1,..., n. Знание ˆθ позволит нам по заданному значению фактора x предсказывать отклик y, точнее, его закономерную часть. Проиллюстрируем основные идеи обработки регрессионного эксперимента (8.3) на примере простой линейной регрессии. Так называют задачу регрессии, в которой x и y — одномерные величины (поэтому мы будем обозначать их x и y), а функция f(x, θ) имеет вид A + bx, где θ = (A, b). В этом случае соотношение (8.3) принимает вид: yi = A + bxi + εi i = 1,..., n. (8.4) Здесь x1,..., xn — заданные числа (значения фактора); y1,..., yn — наблюденные значения отклика; ε1,..., εn — независимые (ненаблюдаемые) одинаково распределенные случайные величины. Гауссовская модель. При решении задачи (8.4) (как и во многих других случаях) используются два основных подхода: непараметрический и гауссовский, они различаются характером предположений относительно закона распределения случайных величин ε. Сначала мы рассмотрим гауссовскую модель простой линейной регрессии. В ней дополнительно к вышесказанному предполагается, что величины εi распределены по нормальному закону N(0, σ2) с некоторой неизвестной дисперсией σ2.
Для определения параметров регрессионной модели часто используется метод наименьших квадратов. Метод наименьших квадратов. При выборе методов определения параметров регрессионной модели можно руководствоваться различными подходами. Один из наиболее естественных и распространенных состоит в том, что при «хорошем» выборе оценки ˆθ параметра модели θ величины yi − f(xi, θ) (в случае простой линейной регрессии — величины yi − A − bxi) должны в совокупности быть близки к нулю. Меру близости совокупности этих величин (они обычно называются остатками) к нулю можно выбирать по-разному (например, максимум модулей, сумму модулей и т.д.), но наиболее простые формулы расчета получаются, если в качестве этой меры выбрать сумму квадратов:
Определение. Методом наименьших квадратов называется способ подбора параметров регрессионной модели исходя из минимизации суммы квадратов остатков. Сам по себе метод наименьших квадратов не связан с какими-либо предположениями о распределении случайных ошибок ε1,..., εn, он может применяться и тогда, когда мы не считаем эти ошибки случайными (например, в задачах сглаживания экспериментальных данных). Однако мы будем рассматривать метод наименьших квадратов в связи с гауссовской моделью. Причины этого следующие: • именно в гауссовской модели метод наименьших квадратов обладает определенными свойствами оптимальности; • в гауссовской модели получаемые с помощью этого метода оценки неизвестных параметров обладают ясными статистическими свойствами.
Средняя точка ( b – коэффициент регрессии
В регрессии с вероятностью 0,95 справедливо равенство:
Если коэффициент регрессии=0, то между x и y отсутствует линейная связь. Если 0 входит в доверительный интервал, то линейной регрессии нет.
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 277; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.202.187 (0.008 с.) |


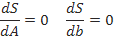





 всегда лежит на линии регрессии.
всегда лежит на линии регрессии.
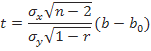
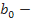 коэффициент истинной регрессии, т.е. регрессии которая м.б. получена по результатам генеральных выборок.
коэффициент истинной регрессии, т.е. регрессии которая м.б. получена по результатам генеральных выборок. – случайная величина, распределенная по закону Стьюдента.
– случайная величина, распределенная по закону Стьюдента.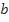 - искомый коэффициент регрессии.
- искомый коэффициент регрессии.



