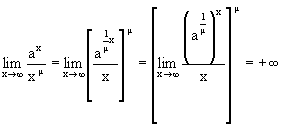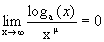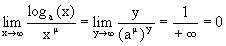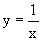Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывность элементарных функций
Разумеется, имеется бесконечно много разных функций. Однако среди них выделяется класс элементарных функций. К ним относятся: а) степенная функция у=xn; б) показательная функция у=ax; в) логарифмическая функция у=loga(x); г) гиперболические функции sh(x), ch(x), th(x); д) тригонометрические функции sin(x), cos(x), tg(x); е) обратные тригонометрические функции arc sin(x), arc cos(x), arc tg(x). Всевозможные суперпозиции этих функций также называются элементарными. Далее небольшой обзор свойств этих функций, особо обращая внимание на их непрерывность. Степенная функция. Функция y=xm, где m – произвольное вещественное число, называется степенной функцией. В общем случае считается, что она определена для x>0, хотя при некоторых частных значениях m (например, когда m - целое число) она имеет смысл и при x<0. Графики этой функции имеют различный вид при разных m. а) 0<m<1
б) m>1
б) m<0
Показательная функция. Функция y=ax называется показательной функцией. Число a является произвольным положительным вещественным числом, т.е. a>0. Функция определена и непрерывна для всех вещественных х. Ее графики имеют различный вид в зависимости от значения а.
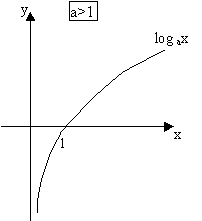
При a>1 y=ax строго монотонно возрастает.
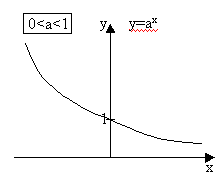
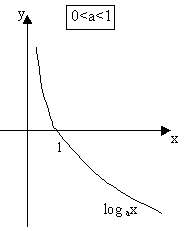
При 0<a<1 y=ax строго монотонно убывает.
Математики особенно "любят" функцию y=ex, т.е. показательную функцию при а=е. Ее называют экспоненциальной функцией, или просто экспонентой. Основным свойством показательной функции является следующее свойство:
Можно показать, что среди непрерывных функций показательная функция – единственная функция, удовлетворяющая свойству f(x1+x2)=f(x1)f(x2). Следствием этого свойства является следующее: (ax)m=axm Гиперболические функции. С функцией ex тесно связаны функции, получившие название гиперболических. К ним относятся: гиперболический синус гиперболический косинус гиперболический тангенс Рассмотрим коротко свойства этих функций.
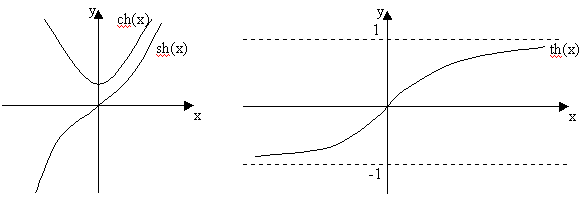
1. Область определения этих функций -¥<x<+¥ 2. sh(-x)= –sh(x) th(-x)= –th(x) ch(-x)= ch(x) т.е. sh(x) и th(x) являются нечетными функциями, а ch(x) – четной функцией. Графики их изображены на рисунках. 3. sh(h), ch(x), и th(x) непрерывны для всех х. 4. sh(x) и th(x) монотонно возрастают. 5. Выведем основные формулы, касающиеся этих функций, и очень напоминающие формулы тригонометрии. а) ch2(x)-sh2(x)=1 Действительно,
б) Вывод этой формулы надо вести с правой части. Имеем:
в) Аналогично имеем:
Можно вывести и много других формул, аналогичных формулам геометрии. Логарифмическая функция. Функция, обратная ax, называется логарифмической функцией, и обозначается logax. Ее свойства получаются как следствия свойств функции ax. а) 1. Так как. значения axÎ(0; +¥), то logax определена для 0<x<+¥. 2. Так как ax строго монотонно возрастает, то logax тоже строго монотонно возрастает. 3. Так как ax строго непрерывна, то и logax тоже непрерывна. 4. logex называется натуральным логарифмом и обозначается ln(x). б) 1. log ax определена для 0<x<+¥. 2. log ax строго монотонно убывает. 3. log ax непрерывна. 4. Основное свойство логарифмической функции имеет вид:
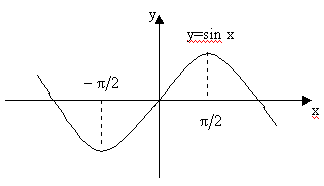
Можно показать, что logax – единственная непрерывная функция, удовлетворяющая свойству Другие важные формулы, касающиеся логарифмической функции а) б) Тригонометрические функции. Т.к. эти функции подробно изучаются в школе, то напоминать их свойства мы не будем. Укажем лишь, что sinus(x) и cos(x) непрерывны для всех x, а Обратные тригонометрические функции. arc sin(x) Рассмотрим график функции у=sin(x) и на этом графике рассмотрим лишь участок
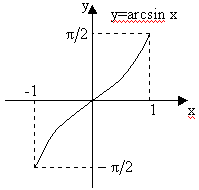
Функция, обратная к sin(x), только на этом участке называется главной ветвью arcsin x. Именно ее мы и будем изучать.
1. Так как –1 £ sin x £ +1, то arcsinx определен для –1 £ x £ +1. 2. Так как на выделенном участке sin x строго монотонно возрастает, то arcsin x тоже строго монотонно возрастает. 3. Так как sin x непрерывна, то и arcsin x тоже непрерывна. 4. 5. arc cos(x)
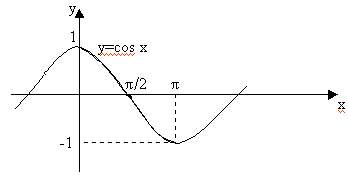
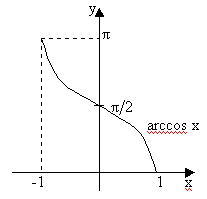
Выделим на графике функции у=cos(x) участок 0£ x £ p. Функцию, обратную к cos x именно на этом участке будем называть главной ветвью arc cos x и именно ее будем изучать и использовать.
1. Так как –1 £ cos x £ +1, то arccos x определен для –1 £ x £ +1. 2. Так как на выделенном участке cos x строго монотонно убывает, то arccos x тоже строго монотонно убывает. 3. Так как на выделенном участке cos x непрерывна, то arccos x тоже непрерывна. 4. arc tg(x) На графике функции у=tg(x) выделим лишь участок
1. arctg x определен для – ¥ < x < + ¥. 2. Так как на выделенном участке tg x строго монотонно возрастает, то arctg x тоже строго монотонно возрастает. 3. Так как на выделенном участке tg x непрерывна, то и arctg x тоже непрерывна. 4. arctg(-x)=-arctg(x) 5.
Замечательные пределы
Рассмотрим еще некоторые пределы, которые полезно знать. 1. Вспомним замечательный предел
Сделаем в нем "замену переменных"
2. Вспомним, что loga – непрерывная функция. Логарифмируя предыдущее равенство, получим:
Итак,
В частности,
3. В предыдущем соотношении сделаем снова замену переменных
Переворачивая это соотношение, получим
В частности,
4. Докажем, что
положим Тогда при x®0 y®0. Далее m ln(1+x)=ln(1+y) Далее имеем
так как оба написанных предела равны 1. 5. Докажем, что при a>1 и при m>0
а) Докажем сначала, что при a>1
Поэтому т.е. б) Возьмем произвольное x®+¥ и обозначим n=[x], т.е. целая часть от x. Тогда n £ x £ n+1 и получаем
так что в) Наконец, при произвольном m>0 имеем
6. Докажем, что при m>0 и a>1
Действительно, делая замену переменных loga(x)=y, x=ay, получим, что при x®+¥, y®+¥
7. Докажем, что при m>0 и a>1
Действительно, делая замену переменных
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 463; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.36.221 (0.024 с.) |
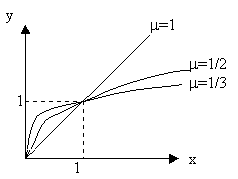 В этом случае y=xm определена для x³ 0. Она является строго монотонно возрастающей функцией и непрерывна для всех x³ 0.
В этом случае y=xm определена для x³ 0. Она является строго монотонно возрастающей функцией и непрерывна для всех x³ 0.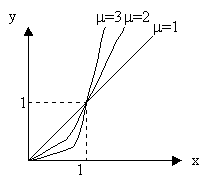 В этом случае y=xm определена для x³ 0. Она является строго монотонно возрастающей функцией и непрерывна для всех x³ 0.
В этом случае y=xm определена для x³ 0. Она является строго монотонно возрастающей функцией и непрерывна для всех x³ 0.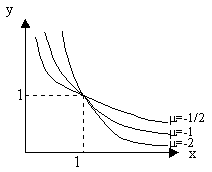 В этом случае y=xm определена для всех x>0 и
В этом случае y=xm определена для всех x>0 и 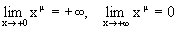 . Она является строго монотонно убывающей функцией и непрерывна для всех x>0.
. Она является строго монотонно убывающей функцией и непрерывна для всех x>0.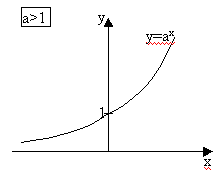
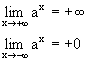
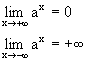
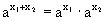

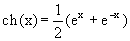
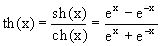
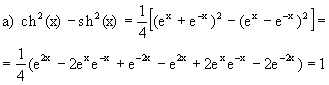
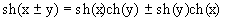
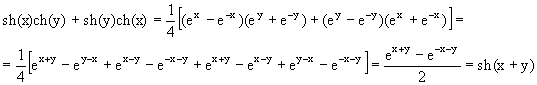
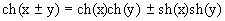
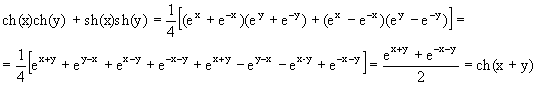
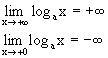
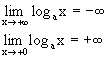
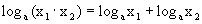
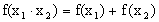 .
.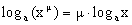
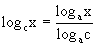
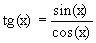 имеет разрывы второго рода в точках, где cos(x)=0, т.е. в точках
имеет разрывы второго рода в точках, где cos(x)=0, т.е. в точках 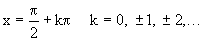
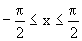 .
.
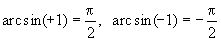
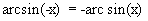
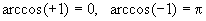
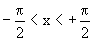 . Функцию, обратную к tg x именно на этом участке будем называть главной ветвью arctg x.
. Функцию, обратную к tg x именно на этом участке будем называть главной ветвью arctg x.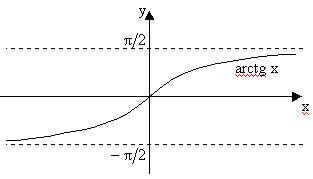
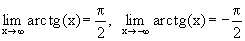
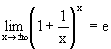
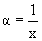 . Тогда при
. Тогда при 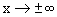
 и мы получим
и мы получим
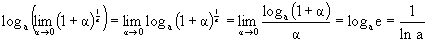
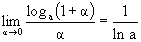
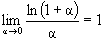
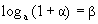 . Тогда при
. Тогда при 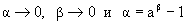 получаем
получаем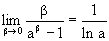
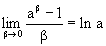 ,
, .
.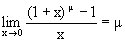
 .
.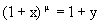 , и логарифмируя это равенство, получим
, и логарифмируя это равенство, получим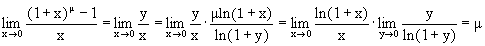
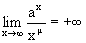
 . Действительно, обозначим a=1+l, l>0. Пользуясь формулами бинома Ньютона, получим
. Действительно, обозначим a=1+l, l>0. Пользуясь формулами бинома Ньютона, получим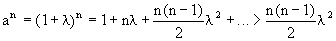 .
.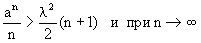 ,,
,,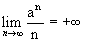 .
. 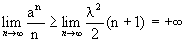
 ,
, . Поэтому
. Поэтому 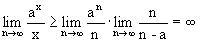 .
.