
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Над матрицами. Матрица, получаемая в результате операции умножения,Стр 1 из 5Следующая ⇒
Линейная алгебра. 1)Матрицы. Основные определения. Транспонирование матриц. 2)Линейные опрации над матрицами. Свойства. 3)Умножение матриц. Свойства. 4)Линейная зависимостьи независимость матриц-строк и матриц-столбцов. 5)Определители n-го порядка. Их свойства. 6)Системы линейных уравнений. Основные определения. 7)Метод Крамера. 8)Обратная матрица. Решение простейших матричных уравнений. Матричный метод решения систем ленейных уравнений. 9)Ранг матрицы. Базисный минор.
_____________Вопрос №1 Линейная алгебра.__________________________________ 1) ----------Матрицы. Основные определения.------------- составленная из m·n чисел, называется матрицей из m строк и n столбцов или матрицей размера m×n, а также m×n-матрицей. Числа aij (i=1,2,...,m;j=1,2,...,n) называются элементами матрицы; первый индекс i указывает номер строки, в которой стоит элемент матрицы, а второй индекс j - номер столбца. Матрица (1) может обозначаться также |aij|, i=1,2,...,m; j=1,2,...,n. Кроме того, для матриц используются обозначения
или (aij);
или [aij]. Если число строк матрицы равно числу ее столбцов (и равно n), то матрица называется квадратной матрицей (порядка n).Две матрицы |aij| и |bij| называются равными, если числа их строк и столбцов соответственно равны и равны числа, стоящие на соответствующих местах: aij=bkl при l=k и j= l Основными арифметическими операциями над матрицами являются умножение матрицы на число, сложение матриц и умножение матрицы. Единичная матрица. Квадратная матрица, все диагональные элементы которой равны единице, а остальные - нули, называется единичной и обозначается E (или En, где n - ее порядок,|ij|, где i,j=1,2,...,n. Символ ij имеет специальное название - "символ Кронекера'').Для любой квадратной матрицы A порядка n справедливо равенство En·A=A·En=A Матрицы |aij| порядка n, у которых aij=0 для всех i/=j, т.е. матрицы вида
называются диагональными элементами матрицами (об элементах a11,a22,...,ann также говорят, что они стоят на главной диагонали). Свойство диагональных матриц. Сумма и произведение двух диагональных матриц - также диагональные матрицы, ---------------Транспонирование матриц. -------------- Пусть A=|aij|- матрица размера m×n: A=|aij| Матрица, получающаяся из матрицы A заменой строк столбцами, называется транспонированной матрицей по отношению к матрице A и обозначается AT.
Квадратная матрица A называется симметрической, если AT=A, и кососимметрической, если AT=−A Элементы, расположенные симметрично относительно главной диагонали, у симметрической матрицы равны, а у кососимметрической противоположны. Все диагональные элементы кососимметрической матрицы равны нулю. Транспонированная матрица — матрица AT, полученная из исходной матрицы A заменой строк на столбцы. Формально, транспонированная матрица для матрицы A размеров — матрица AT размеров, определённая как AT[i, j] = A[j, i]. Например,
Свойства транспонированных матриц
Дважды транспонированная матрица А равна исходной матрице А.
Транспонированная сумма матриц равна сумме транспонированных матриц.
Транспонированное произведение матриц равно произведению транспонированных матриц
При транспонировании можно выносить скаляр.
Определитель транспонированной матрицы равен определителю исходной матрицы.
2) Линейные операции над матрицами. 1. Сложение матриц. Определение 3.4. Суммой матриц А и В одинаковой размерности m х n называется матрица С той же размерности, каждый элемент которой равен сумме элементов матриц А и В, стоящих на тех же местах: Свойства сложения: 1. А + В = В + А. 2. (А + В) + С = А + (В + С). 3. Если О – нулевая матрица, то А + О = О + А = А Пример. 2. Умножение матрицы на число. Свойства умножения матрицы на число: 1. (km)A=k(mA). 2. k(A + B) = kA + kB. 3. (k + m)A = kA + mA. Пример. Перемножение матриц. Выше было указано, что сложение матриц накладывает условия на размерности слагаемых. Умножение матрицы на матрицу тоже требует выполнения определенных условий для размерностей сомножителей, а именно: число столбцов первого множителя должно равняться числу строк второго. Определение. Произведением матрицы А размерности m х p и матрицы В размерности p х n называется матрица С размерности m х n, каждый элемент которой определяется формулой:
элементов i-й cтроки матрицы А на соответствующие элементы j-го столбца матрицы В. Пример.
Размерность матрицы С=АВ составляет 2 х 3 Найдем элементы матрицы С:
Итак, произведению их определителей. Замечание. Операция перемножения матриц некоммутативна, т.е. AB не равно BA Действительно, если существует произведение АВ, то ВА может вообще не существовать из-за несовпадения размерностей (см. предыдущий пример). Если существуют и АВ, и ВА, то они могут иметь разные размерности (еслиm не равно n).Для квадратных матриц одного порядка произведения АВ и ВА существуют и имеют одинаковую размерность, но их соответствующие элементы в общем случае не равны. Однако в некоторых случаях произведения АВ и ВА совпадают. Рассмотрим произведение квадратной матрицы А на единичную матрицу Е того же порядка:
Тот же результат получим и для произведения ЕА. Итак, для любой квадратной матрицы А АЕ = ЕА =А. Обратная матрица. Определение 3.7. Квадратная матрица А называется вырожденной, если Определение 3.8. Квадратная матрица В называется обратной к квадратной матрице А того же порядка, если АВ = ВА = Е. При этом В обозначается A-1. Рассмотрим условие существования матрицы, обратной к данной, и способ ее вычисления. Теорема. Для существования обратной матрицы необходимо и достаточно, чтобы исходная матрица была невырожденной. Доказательство. 1) Необходимость: так как 2) Достаточность: зададим матрицу A-1 в следующем виде:
Тогда любой элемент произведения A* A-1 (или A-1 *A), не лежащий на главной диагонали, равен сумме произведений элементов одной строки (или столбца) матрицы А на алгебраические дополнения к элементам друго столбца и, следовательно, равен 0 (как определитель с двумя равными столбцами). Элементы, стоящие на главной диагонали, равны обратной матрицы: ее элементами являются алгебраические дополнения к элементам транспонированной матрицы А, деленные на ее определитель. Пример. Найдем матрицу, обратную к дополнения к ее элементам: дополнения к элементам строки матрицы А образуют в обратной матрице столбец с тем же номером. Итак, Можно убедиться, что найденная матрица действительно удовлетворяет определению A-1 Найдем Тот же результат получим и при перемножении в обратном порядке.
Тогда систему (2.3) можно записать в виде матричного уравнения: АХ = В (3.1) Пусть матрица А – невырожденная, тогда существует обратная к ней матрица A-1 Умножим обе части равенства (3.1) слева на A-1 Получим --------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- 3)[править] Умноже́ние ма́триц — одна из основных операций Решение матричных уравнений Матричные уравнения могут иметь вид: АХ = В, ХА = В, АХВ = С,
где А,В,С — задаваемые матрицы, Х- искомая матрица. Определения Определение 1. Функция f(x) называется непрерывной в точке x0, если Дадим несколько расшифровок этого важнейшего определения. а) Вспоминая понятие предела, запишем непрерывность f(x) в точке х0 в виде
б) Так как х0=lim x, то непрерывность в точке х0 можно записать в виде
Отсюда следует важнейшее свойство непрерывной функции: для непрерывной функции можно переставлять местами знак функции и знак предельного перехода
в) Обозначим Dx=x-x0 (приращение аргумента) и Df=f(x)-f(x0) (приращение функции). Тогда непрерывность в точке х0 означает, что Введем обозначения:
если эти пределы существуют. Определение 2. Функция f(x) называется непрерывной в точке х0 слева (справа) если f(x0)=f(x0 – 0) (f(x0)=f(x0+0)). Очевидно,что непрерывность в точке х0 означает непрерывность слева и справа одновременно. Определение 3. Функция f(x) называется непрерывной на некотором множестве Х, если она непрерывна в каждой точке этого множества, т.е. если
Обратите внимание, где стоит квантор Определение. Если функция f(x) не является непрерывной в точке х0, то говорят, что в точке х0 функция f(x) имеет разрыв.
Типы разрывов</H2< a> А. Пусть существуют конечные f(x0-0) и f(x0+0), но они не равны друг другу График функции f(x) в окрестности точки х0 имеет в этом случае примерно такой вид:
Величина |f(x0+0)-f(x0-0)| называется величиной скачка функции f(x) в точке х0. Б. Если хотя бы один из пределов Виды графика функции f(x) в окрестности точки х0 в этом случае гораздо разнообразнее. Некоторые возможные варианты приведены ниже.
Монотонные функции Докажем теперь две теоремы, касающиеся непрерывности монотонных функций. Теорема 1.. Пусть f(x) определена и монотонна на замкнутом отрезке [a,b]. Тогда она может иметь на этом отрезке только разрывы I рода (скачки). Доказательство. Пусть, для определенности, f(x) монотонно возрастает.
При движении к х0 справа значения f(x) будут монотонно убывать, но будут ограничены снизу величиной f(x0). Поэтому снова существует конечный Если f(x0+0)= f(x0-0), то f(x) будет непрерывна в точке х0, если же f(x0+0)<f(x0-0), то у f(x) в точке х0 будет разрыв I рода. < Определение. Говорят, что значения функции f(x), определенной на <a,b>, заполняют некоторый отрезок <c,d> сплошь, если
Теорема 2. Для того, чтобы монотонная функция f(x) была непрерывной на [a,b], необходимо и достаточно, чтобы ее значения заполняли отрезок [f(a), f(b)] сплошь. Доказательство. Пусть, для определенности, f(x) монотонно возрастает. 1. Пусть f(x) непрерывна на [a,b]. Тогда 2. Пусть f(x) не является непрерывной на [a,b]. Тогда она на [a,b] может иметь только разрывы I рода. Пусть х0 – координата такого разрыва. Возможные поведения графика f(x) изображены на рисунках.
Из них видно, что в этом случае отрезок [f(a), f(b)] заполнен не сплошь. <
Замечательные пределы
Рассмотрим еще некоторые пределы, которые полезно знать. 1. Вспомним замечательный предел
Сделаем в нем "замену переменных"
2. Вспомним, что loga – непрерывная функция. Логарифмируя предыдущее равенство, получим:
Итак,
В частности,
3. В предыдущем соотношении сделаем снова замену переменных
Переворачивая это соотношение, получим
В частности,
4. Докажем, что
положим Тогда при x®0 y®0. Далее m ln(1+x)=ln(1+y) Далее имеем
так как оба написанных предела равны 1. 5. Докажем, что при a>1 и при m>0
а) Докажем сначала, что при a>1
Поэтому т.е. б) Возьмем произвольное x®+¥ и обозначим n=[x], т.е. целая часть от x. Тогда n £ x £ n+1 и получаем
так что в) Наконец, при произвольном m>0 имеем
6. Докажем, что при m>0 и a>1
Действительно, делая замену переменных loga(x)=y, x=ay, получим, что при x®+¥, y®+¥
7. Докажем, что при m>0 и a>1
Действительно, делая замену переменных
Определение Пусть Тогда по определению рангом матрицы A является:ноль, если A — нулевая матрица; число ему минор порядка (r + 1), если они существуют.
Линейная алгебра. 1)Матрицы. Основные определения. Транспонирование матриц. 2)Линейные опрации над матрицами. Свойства. 3)Умножение матриц. Свойства. 4)Линейная зависимостьи независимость матриц-строк и матриц-столбцов. 5)Определители n-го порядка. Их свойства. 6)Системы линейных уравнений. Основные определения. 7)Метод Крамера. 8)Обратная матрица. Решение простейших матричных уравнений. Матричный метод решения систем ленейных уравнений. 9)Ранг матрицы. Базисный минор.
_____________Вопрос №1 Линейная алгебра.__________________________________ 1) ----------Матрицы. Основные определения.------------- составленная из m·n чисел, называется матрицей из m строк и n столбцов или матрицей размера m×n, а также m×n-матрицей. Числа aij (i=1,2,...,m;j=1,2,...,n) называются элементами матрицы; первый индекс i указывает номер строки, в которой стоит элемент матрицы, а второй индекс j - номер столбца. Матрица (1) может обозначаться также |aij|, i=1,2,...,m; j=1,2,...,n. Кроме того, для матриц используются обозначения
или (aij);
или [aij]. Если число строк матрицы равно числу ее столбцов (и равно n), то матрица называется квадратной матрицей (порядка n).Две матрицы |aij| и |bij| называются равными, если числа их строк и столбцов соответственно равны и равны числа, стоящие на соответствующих местах: aij=bkl при l=k и j= l Основными арифметическими операциями над матрицами являются умножение матрицы на число, сложение матриц и умножение матрицы. Единичная матрица. Квадратная матрица, все диагональные элементы которой равны единице, а остальные - нули, называется единичной и обозначается E (или En, где n - ее порядок,|ij|, где i,j=1,2,...,n. Символ ij имеет специальное название - "символ Кронекера'').Для любой квадратной матрицы A порядка n справедливо равенство En·A=A·En=A Матрицы |aij| порядка n, у которых aij=0 для всех i/=j, т.е. матрицы вида
называются диагональными элементами матрицами (об элементах a11,a22,...,ann также говорят, что они стоят на главной диагонали). Свойство диагональных матриц. Сумма и произведение двух диагональных матриц - также диагональные матрицы, ---------------Транспонирование матриц. -------------- Пусть A=|aij|- матрица размера m×n: A=|aij| Матрица, получающаяся из матрицы A заменой строк столбцами, называется транспонированной матрицей по отношению к матрице A и обозначается AT. Квадратная матрица A называется симметрической, если AT=A, и кососимметрической, если AT=−A Элементы, расположенные симметрично относительно главной диагонали, у симметрической матрицы равны, а у кососимметрической противоположны. Все диагональные элементы кососимметрической матрицы равны нулю. Транспонированная матрица — матрица AT, полученная из исходной матрицы A заменой строк на столбцы. Формально, транспонированная матрица для матрицы A размеров — матрица AT размеров, определённая как AT[i, j] = A[j, i]. Например,
Свойства транспонированных матриц
Дважды транспонированная матрица А равна исходной матрице А.
Транспонированная сумма матриц равна сумме транспонированных матриц.
Транспонированное произведение матриц равно произведению транспонированных матриц
При транспонировании можно выносить скаляр.
Определитель транспонированной матрицы равен определителю исходной матрицы.
2) Линейные операции над матрицами. 1. Сложение матриц. Определение 3.4. Суммой матриц А и В одинаковой размерности m х n называется матрица С той же размерности, каждый элемент которой равен сумме элементов матриц А и В, стоящих на тех же местах: Свойства сложения: 1. А + В = В + А. 2. (А + В) + С = А + (В + С). 3. Если О – нулевая матрица, то А + О = О + А = А Пример. 2. Умножение матрицы на число. Свойства умножения матрицы на число: 1. (km)A=k(mA). 2. k(A + B) = kA + kB. 3. (k + m)A = kA + mA. Пример. Перемножение матриц. Выше было указано, что сложение матриц накладывает условия на размерности слагаемых. Умножение матрицы на матрицу тоже требует выполнения определенных условий для размерностей сомножителей, а именно: число столбцов первого множителя должно равняться числу строк второго. Определение. Произведением матрицы А размерности m х p и матрицы В размерности p х n называется матрица С размерности m х n, каждый элемент которой определяется формулой:
элементов i-й cтроки матрицы А на соответствующие элементы j-го столбца матрицы В. Пример. Размерность матрицы С=АВ составляет 2 х 3 Найдем элементы матрицы С:
Итак, произведению их определителей. Замечание. Операция перемножения матриц некоммутативна, т.е. AB не равно BA Действительно, если существует произведение АВ, то ВА может вообще не существовать из-за несовпадения размерностей (см. предыдущий пример). Если существуют и АВ, и ВА, то они могут иметь разные размерности (еслиm не равно n).Для квадратных матриц одного порядка произведения АВ и ВА существуют и имеют одинаковую размерность, но их соответствующие элементы в общем случае не равны. Однако в некоторых случаях произведения АВ и ВА совпадают. Рассмотрим произведение квадратной матрицы А на единичную матрицу Е того же порядка:
Тот же результат получим и для произведения ЕА. Итак, для любой квадратной матрицы А АЕ = ЕА =А. Обратная матрица. Определение 3.7. Квадратная матрица А называется вырожденной, если Определение 3.8. Квадратная матрица В называется обратной к квадратной матрице А того же порядка, если АВ = ВА = Е. При этом В обозначается A-1. Рассмотрим условие существования матрицы, обратной к данной, и способ ее вычисления. Теорема. Для существования обратной матрицы необходимо и достаточно, чтобы исходная матрица была невырожденной. Доказательство. 1) Необходимость: так как 2) Достаточность: зададим матрицу A-1 в следующем виде:
Тогда любой элемент произведения A* A-1 (или A-1 *A), не лежащий на главной диагонали, равен сумме произведений элементов одной строки (или столбца) матрицы А на алгебраические дополнения к элементам друго столбца и, следовательно, равен 0 (как определитель с двумя равными столбцами). Элементы, стоящие на главной диагонали, равны обратной матрицы: ее элементами являются алгебраические дополнения к элементам транспонированной матрицы А, деленные на ее определитель. Пример. Найдем матрицу, обратную к дополнения к ее элементам: дополнения к элементам строки матрицы А образуют в обратной матрице столбец с тем же номером. Итак, Можно убедиться, что найденная матрица действительно удовлетворяет определению A-1 Найдем Тот же результат получим и при перемножении в обратном порядке.
Тогда систему (2.3) можно записать в виде матричного уравнения: АХ = В (3.1) Пусть матрица А – невырожденная, тогда существует обратная к ней матрица A-1 Умножим обе части равенства (3.1) слева на A-1 Получим --------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- 3)[править] Умноже́ние ма́триц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведе́нием ма́триц Свойства Сочетательное свойство:
Распределительное свойство:
Произведение матрицы на единичную матрицу подходящего порядка равно самой матрице:
Произведение матрицы на нулевую матрицу подходящей размерности равно нулевой матрице:
Если произведение матриц обладает ещё рядом свойств. Умножение матриц в целом некоммутативно:
Если перестановочными или коммутирующими между собой. Определитель и след произведения не зависят от порядка умножения матриц:
5)Свойства определителя n -го порядка Свойство 1. При замене строк столбцами (транспонировании) значение определителя не изменится, т.е.
(строка или столбец) состоит из нулей, то определитель равен нулю. Доказательство очевидно. В самом деле, тогда в каждом члене определителя один из множителей будет нуль. Свойство 3. Если в определителе поменять местами два соседних параллельных ряда (строки или столбцы), то определитель поменяет знак на противоположный, т.е.
два одинаковых параллельных ряда, то определитель равен нулю:
ряда пропорциональны, то определитель равен нулю:
одном ряду, умножить на одно и то же число, то значение определителя изменится в это число раз:
одного ряда, можно вынести за знак определителя, например:
одного ряда представлены в виде суммы двух слагаемых, то он равен сумме двух определителей:
прибавить произведение соответствующих элементов параллельного ряда на постоянный множитель, то значение определителя не изменится:
элементам i -го ряда прибавить линейную комбинацию соответствующих элементов нескольких параллельных рядов, то значение определителя не изменится:
Справедливость этого равенства вытекает из свойства 8.
6)Системы линейных уравнений: основные понятия Определение. Система линейных уравнений — это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:
что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.Определение. Решение системы уравнений — это последовательность чисел (k1, k2,..., kn), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x1, x2,..., xn дает верное числовое равенство. Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая: Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.
|
||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.128.39 (0.31 с.) |



 и
и 
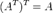




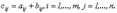
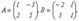
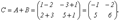
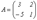 . Тогда
. Тогда 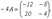
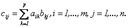 Таким образом, элемент Cij представляет собой сумму произведений
Таким образом, элемент Cij представляет собой сумму произведений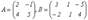 . При этом существует произведение АВ, но не существует произведение ВА.
. При этом существует произведение АВ, но не существует произведение ВА.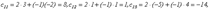
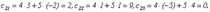
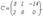 Теорема (без доказательства). Определитель произведения двух квадратных матриц равен
Теорема (без доказательства). Определитель произведения двух квадратных матриц равен
 , и невырожденной, если
, и невырожденной, если 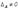
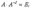 то
то  (теорема 1), поэтому
(теорема 1), поэтому 

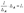 Таким образом,
Таким образом,  . Теорема доказана. Замечание. Сформулируем еще раз способ вычисления
. Теорема доказана. Замечание. Сформулируем еще раз способ вычисления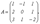
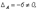 следовательно, матрица А невырожденная. Найдем алгебраические
следовательно, матрица А невырожденная. Найдем алгебраические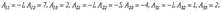 Не забудем, что алгебраические
Не забудем, что алгебраические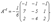
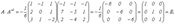 Решение линейных систем с помощью обратной матрицы.Рассмотрим линейную систему
Решение линейных систем с помощью обратной матрицы.Рассмотрим линейную систему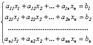 и введем следующие обозначения:
и введем следующие обозначения: 
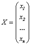 - столбец неизвестных,
- столбец неизвестных,  - столбец свободных членов.
- столбец свободных членов.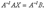 Но
Но 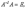 тогда
тогда  , а поскольку
, а поскольку 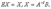 (3.2)
(3.2)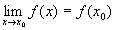 .
.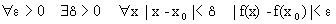
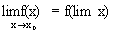

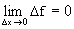 , т.е. бесконечно-малому приращению аргумента соответствует бесконечно-малое приращение функции.
, т.е. бесконечно-малому приращению аргумента соответствует бесконечно-малое приращение функции.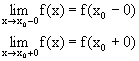
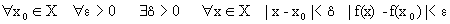
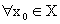 , это важно.
, это важно.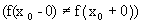 . Тогда говорят, что в точке х0функция f(x) имеет разрыв I рода или скачек.
. Тогда говорят, что в точке х0функция f(x) имеет разрыв I рода или скачек.
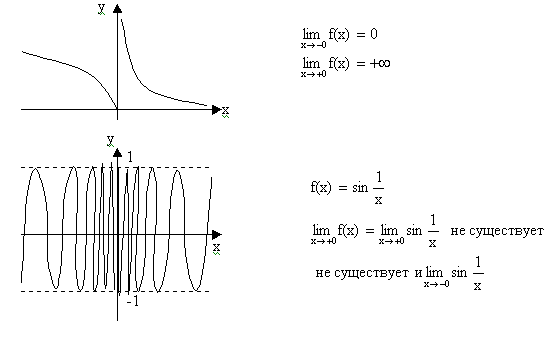
 бесконечен или не существует, то говорят, что в точке х0 функция f(x) имеет разрыв второго рода.
бесконечен или не существует, то говорят, что в точке х0 функция f(x) имеет разрыв второго рода.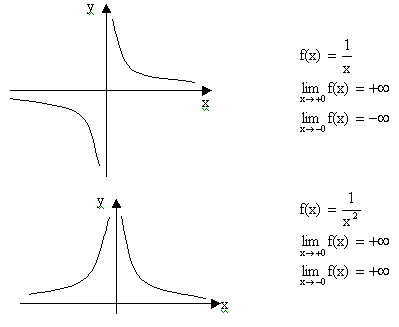
 Возьмем какую-то точку x0 Î[a,b]. Пусть мы приближаемся к точке х0 слева (см. рис.). Тогда при этом значения функции f(x) будут монотонно возрастать. Но они будут ограничены сверху, например, величиной f(x0). Поэтому, по теореме о пределе монотонно-возрастающей функции будет существовать конечный
Возьмем какую-то точку x0 Î[a,b]. Пусть мы приближаемся к точке х0 слева (см. рис.). Тогда при этом значения функции f(x) будут монотонно возрастать. Но они будут ограничены сверху, например, величиной f(x0). Поэтому, по теореме о пределе монотонно-возрастающей функции будет существовать конечный 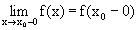 .
.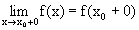 .
.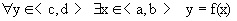 .
. . Согласно второй теореме Больцано-Коши,
. Согласно второй теореме Больцано-Коши, 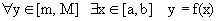 . Поэтому отрезок [f(a),f(b)] заполнен сплошь.
. Поэтому отрезок [f(a),f(b)] заполнен сплошь.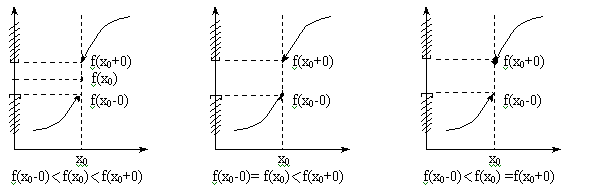
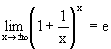
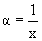 . Тогда при
. Тогда при 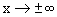
 и мы получим
и мы получим
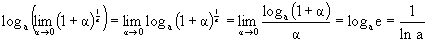
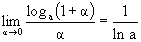
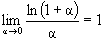
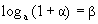 . Тогда при
. Тогда при 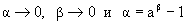 получаем
получаем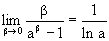
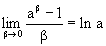 ,
, .
.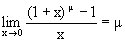
 .
.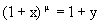 , и логарифмируя это равенство, получим
, и логарифмируя это равенство, получим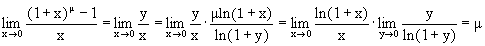
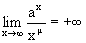
 . Действительно, обозначим a=1+l, l>0. Пользуясь формулами бинома Ньютона, получим
. Действительно, обозначим a=1+l, l>0. Пользуясь формулами бинома Ньютона, получим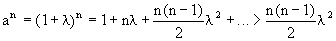 .
.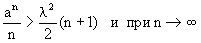 ,,
,,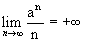 .
. 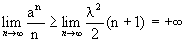
 ,
, . Поэтому
. Поэтому 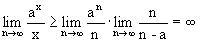 .
.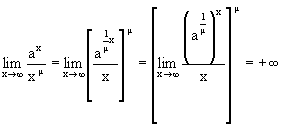
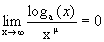
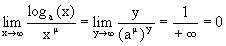

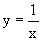

 — прямоугольная матрица.
— прямоугольная матрица. , где Mr — минор матрицы A порядка r, а Mr + 1 — окаймляющий к н
, где Mr — минор матрицы A порядка r, а Mr + 1 — окаймляющий к н порядка k равны нулю (Mk = 0).
Тогда
порядка k равны нулю (Mk = 0).
Тогда 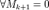 , если они существуют. Связанные определения Базисный минор
, если они существуют. Связанные определения Базисный минор
 матрицы M размера
матрицы M размера 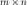 называют полным, если
называют полным, если  .
.
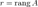 . Строки и столбцы, на
. Строки и столбцы, на
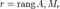 — базисный минор матрицы A, тогда: базисные строки и базисные столбцы линейно независимы;
— базисный минор матрицы A, тогда: базисные строки и базисные столбцы линейно независимы;
 , то строки и столбцы этой матрицы линейно зависимы. Пусть
, то строки и столбцы этой матрицы линейно зависимы. Пусть  , тогда максимальное количество
, тогда максимальное количество
 над полем C (или R). Пусть T — линейное преобр
азование, соответствующее A в стандартном базисе; это значит, что T (x) = Ax. Ранг матрицы A — это размерность области
значений преобразования T.
над полем C (или R). Пусть T — линейное преобр
азование, соответствующее A в стандартном базисе; это значит, что T (x) = Ax. Ранг матрицы A — это размерность области
значений преобразования T.

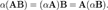

 .
.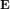




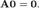
 и
и  — квадратные одного и того же порядка, то
— квадратные одного и того же порядка, то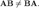
 , то матрицы
, то матрицы  называются
называются

 Свойство 2. Если хотя бы один ряд
Свойство 2. Если хотя бы один ряд Свойство 4. Если в определителе имеются
Свойство 4. Если в определителе имеются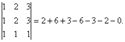 Свойство 5. Если в определителе два параллельных
Свойство 5. Если в определителе два параллельных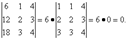 Свойство 6. Если все элементы определителя, стоящие в
Свойство 6. Если все элементы определителя, стоящие в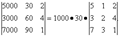 Следствие. Общий множитель, содержащийся во всех элементах
Следствие. Общий множитель, содержащийся во всех элементах Свойство 7. Если в определителе все элементы
Свойство 7. Если в определителе все элементы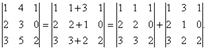 Свойство 8. Если к элементам какого-либо ряда
Свойство 8. Если к элементам какого-либо ряда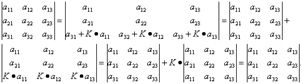 Свойство 9. Если к
Свойство 9. Если к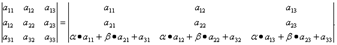
 Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают,
Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают,


