
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторы. Линейные операции над векторами ⇐ ПредыдущаяСтр 7 из 7
Пусть в пространстве даны точки A и B. соединяющий их отрезок, называется направленным отрезком, если одна из точек считается его началом, а другая – концом. Если A – начало, а B – конец, то такой направленный отрезок обозначается Два вектора называются коллинеарными, если они параллельны или ле- жат на одной прямой. Коллинеарность векторов обозначается значком | |. Коллинеарные векторы могут быть сонаправленными (↑↑) или противоположно направленными (↑↓). Векторы Равные векторы можно получить друг из друга при помощи параллельного переноса. В дальнейшем будем отождествлять равные векторы, считая их одним и тем же вектором, отложенным от разных точек пространства.
Обычно в связи с таким изменением понятия вектора недоразумений не возникает.
Пусть имеется два вектора:
Чтобы умножить вектор Умножение вектора на число тесно связано с коллинеарностью векторов. для того чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы один из них отличался от другого числовым множителем. Сложение векторов и умножение вектора на число, то есть линейные операции над векторами, обладают следующими свойствами:
1. 2. 3. 4. 5. 6. 7. 8. Рисунки а), б), в) и г) иллюстрируют первое, второе, восьмое и четвёртое свойства. Рисунок а) показывает также, что векторы можно складывать по правилу параллелограмма: суммой векторов, приведённых к одному началу, служит диагональ параллелограмма, построенного на этих векторах. В силу свойств 1 – 8 множество векторов с введёнными для его элементов линейными операциями является линейным пространством. Координаты вектора Пусть в пространстве введена декартова система координат OXYZ – три взаимно перпендикулярные оси OX, OY, OZ с началом в точке O.
Из произвольной точки пространства A опустим перпендикуляр Координаты Для того чтобы определить координаты
Координаты вектора служат коэффициентами при разложении его по базису то есть Покажем, как получается такое равенство. Так как вектор Поэтому Следствием формулы разложения вектора по базису является утверждение о равенстве векторов, имеющих одинаковые координаты. При сложении векторов их координаты складываются. При умножении вектора на число, его координаты умножаются на это же число. Эти утверждения примем на веру, без доказательства. Выпишем их кратко, в виде формул:
Следствием этих утверждений являются формулы выражения координат вектора через координаты конца и начала и условие коллинеарности векторов. Остановимся на этом подробнее. Пусть даны точки Условие коллинеарности векторов Эту формулу используют и тогда, когда знаменатель одной из дробей равен нулю, считая, что и числитель этой дроби должен быть равен нулю.
Зная координаты вектора можно найти его длину. По теореме Пифагора
В заключение обсудим вопрос о связи геометрических и алгебраических векторов. Каждому вектору сопоставляется тройка чисел – его координаты. С другой стороны, любая тройка чисел, то есть алгебраический вектор, может рассматриваться как координаты вектора, и, следовательно, определяет геометрический вектор. Соответствие между геометрическими и алгебраическими векторами взаимно однозначное и сохраняется при линейных операциях над ними. Вот почему и те, и другие называются векторами. Если принять соглашение об отождествлении геометрического вектора
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.17.20 (0.026 с.) |

 B
A
B
A 

 называются равными (
называются равными ( ), если
), если  (они сонаправлены) и
(они сонаправлены) и  (равны по длине). Равенство векторов обладает следующими свойствами: каждый вектор равен самому себе; если вектор
(равны по длине). Равенство векторов обладает следующими свойствами: каждый вектор равен самому себе; если вектор  , то
, то 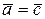 .
.




 Исходная позиция Новая точка зрения
Исходная позиция Новая точка зрения

 . Один и тот же вектор, отложенный
от разных точек пространства
. Один и тот же вектор, отложенный
от разных точек пространства
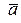





 .
.







 . Если же
. Если же  , то длину вектора
, то длину вектора  раз и изменить его направление на противоположное.
раз и изменить его направление на противоположное.







 а)
а) 









 в)
в)


 г)
г)











 ,
, ,
, ,
, ,
, ,
, Z
Z 











 O
O  Y
Y

 X
X
 на плоскость XOY. Затем из точки
на плоскость XOY. Затем из точки 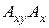 и
и  на оси OX и OY, соответственно. По теореме о трёх перпендикулярах
на оси OX и OY, соответственно. По теореме о трёх перпендикулярах  ,
,  . На оси OZ отложим отрезок
. На оси OZ отложим отрезок  , равный
, равный  – прямоугольник,
– прямоугольник, 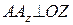 . Таким образом, точки
. Таким образом, точки  являются основаниями перпендикуляров, опущенных из точки A на координатные оси.
являются основаниями перпендикуляров, опущенных из точки A на координатные оси. ,
,  ,
,  точки A в системе координат OXYZ вводятся следующим образом: абсцисса
точки A в системе координат OXYZ вводятся следующим образом: абсцисса 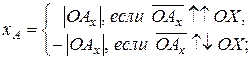 ордината
ордината 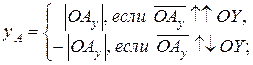 аппликата
аппликата 
 ,
,  ,
,  вектора
вектора  . За координаты вектора
. За координаты вектора 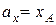 ,
, 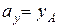 ,
,  (это не противоречит общепринятому определению координат как проекций вектора на оси). Координаты вектора записываются в скобках рядом с его обозначением,
(это не противоречит общепринятому определению координат как проекций вектора на оси). Координаты вектора записываются в скобках рядом с его обозначением, 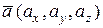 .
.
 Z
Z 











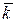

 ,
,  ,
,  ),
), .
.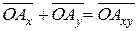 и
и  ,
, . Очевидно, что
. Очевидно, что  ,
,  ,
,  . Но
. Но  .
.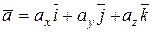 .
.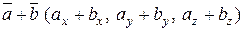 ,
,  .
. и
и  . Рассмотрим вектор
. Рассмотрим вектор  . Очевидно,
. Очевидно,  , откуда
, откуда  и, следовательно,
и, следовательно,  . Аналогично получаем, что
. Аналогично получаем, что  ,
, 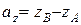 . Итак, чтобы найти координаты вектора
. Итак, чтобы найти координаты вектора  (
( ) или, в координатах,
) или, в координатах,  ,
,  ,
,  , откуда
, откуда  . Таким образом, условие коллинеарности векторов
. Таким образом, условие коллинеарности векторов  состоит в пропорциональности их координат:
состоит в пропорциональности их координат:  .
. Z
Z 
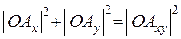 (из
(из  и равенства
и равенства  ) и
) и  (из
(из  и равенства
и равенства  ). Отсюда
). Отсюда  . Это значит, что
. Это значит, что и
и  .
.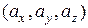 , допустима запись
, допустима запись 


