
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные пространства и линейные операторы
Линейные пространства Множество L называется линейным пространством, если для его элементов определены операции сложения и умножения на число, обладающие следующими свойствами: 1) для любых x и y, принадлежащих L, 2) для любых x, y и z, принадлежащих L, 3) существует элемент, обозначаемый через 4) для каждого x из L существует противоположный элемент, обозначаемый через 5) для каждого x из L умножение на единицу даёт тот же x, то есть 6) для любых чисел α, β и любого x, принадлежащего L, 7) для любых чисел α, β и любого x, принадлежащего L, 8) для любого числа α и любых x и y, принадлежащих L, Ещё два свойства, Для доказательства второго представим Примером линейного пространства может служить множество матриц одинаковой размерности, в том числе множество n -мерных алгебраических векторов. Пусть Элементы Если же можно указать такие, одновременно не равные нулю, коэффициенты Пусть в линейном пространстве L имеются n линейно независимых элементов В этом случае совокупность элементов Представление элемента линейного пространства в виде линейной комбинации базисных элементов называется разложением этого элемента по базису. Координаты элемента x относительно данного базиса определяются однозначно. Действительно, пусть имеется два разложения элемента x по базису,
Таким образом, если в n -мерном линейном пространстве L выбран базис, каждому элементу x этого пространства сопоставляется алгебраический вектор X – набор его координат, то есть Рассмотрим условие линейной независимости k элементов n -мерного линейного пространства L. Пусть элементы
Т е о р е м а. Любая совокупность n линейно независимых элементов n -мерного линейного пространства L является базисом. Доказательство. Пусть элементы
Главный определитель этой системы отличен от нуля, так как матрица коэффициентов составлена из координат линейно независимых элементов и имеет ранг, равный их количеству. Следовательно, система имеет решение (притом единственное). Если матрицы Равенство Линейные операторы Пусть каждому элементу x из некоторого линейного пространства L поставлен вполне определённый элемент y = A (x) из линейного пространства M, причём A (x 1+ x 2) = A (x 1) + A (x 2) и A (λ x)= λ A (x), где λ – число. Тогда говорят, что на линейном пространстве L задан линейный оператор A со значениями в M. Если L и M конечномерны, n и m – их размерности, а Пусть A (e i)= + …+ xn ( Таким образом, y = A (x) представляется в базисе так что действие оператора A действительно сводится к умножению слева столбца X на матрицу A. Если линейный оператор действует из L в L, то матрица A будет квадратной. В дальнейшем, учитывая, что Собственными векторами и собственными числами линейного оператора, действующего из L в L, называются собственные векторы и собственные числа соответствующей матрицы. примером линейного оператора может служить перестановка двух координат вектора X, xi и xj. Матрицей такого оператора является матрица, получающаяся из единичной перестановкой i -го и j -го столбцов. Скажем, чтобы поменять местами четвёртый и первый элементы вектора (–4, 0, –6, 7, 3)Τ (числа 7 и – 4), достаточно умножить его слева на матрицу Квадратичные формы
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.158.148 (0.013 с.) |
 ;
; ;
; , такой, что
, такой, что 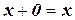 для любого x из L;
для любого x из L; , такой, что
, такой, что  ;
;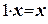 ;
; ;
; ;
; .
. и
и 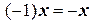 , можно вывести. Покажем это. Из 5) и 7) следует, что
, можно вывести. Покажем это. Из 5) и 7) следует, что  . Тогда
. Тогда  , откуда
, откуда  , то есть
, то есть  . Первое из двух свойств доказано.
. Первое из двух свойств доказано. как
как 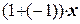 =
=  . Затем, прибавив – x к обеим частям равенства
. Затем, прибавив – x к обеим частям равенства  , откуда
, откуда  и, следовательно,
и, следовательно,  .
. – элементы линейного пространства L. Выражение
– элементы линейного пространства L. Выражение  , где
, где  – какие-то числа, называется линейной комбинацией элементов
– какие-то числа, называется линейной комбинацией элементов  называются линейно независимыми, если из равенства
называются линейно независимыми, если из равенства  следует, что
следует, что  .
. , что соответствующая линейная комбинация обращается в
, что соответствующая линейная комбинация обращается в  , элементы
, элементы 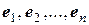 , обладающих тем свойством, что любой элемент x из этого пространства является их линейной комбинацией с коэффициентами
, обладающих тем свойством, что любой элемент x из этого пространства является их линейной комбинацией с коэффициентами  .
. – координатами элемента x относительно этого базиса, число n – размерностью пространства, а само пространство L – n - мерным линейным пространством.
– координатами элемента x относительно этого базиса, число n – размерностью пространства, а само пространство L – n - мерным линейным пространством. и
и  . Вычтем из первого равенства второе. Получим
. Вычтем из первого равенства второе. Получим  . Так как
. Так как  линейно независимы,
линейно независимы,  , следовательно,
, следовательно,  , то есть коэффициенты этих разложений совпадают.
, то есть коэффициенты этих разложений совпадают. . А поскольку при сложении элементов их координаты, очевидно, складываются, а при умножении на число – умножаются на число, элемент x можно отождествить с вектором X. Поэтому линейное пространство часто называют линейным векторным пространством, а его элементы – векторами.
. А поскольку при сложении элементов их координаты, очевидно, складываются, а при умножении на число – умножаются на число, элемент x можно отождествить с вектором X. Поэтому линейное пространство часто называют линейным векторным пространством, а его элементы – векторами. в базисе
в базисе  через
через  (i =1,2,…, k). Предположим, что какая-то линейная комбинация элементов
(i =1,2,…, k). Предположим, что какая-то линейная комбинация элементов  обращается в ноль,
обращается в ноль,  . Поскольку
. Поскольку  должны обращаться в 0. Это значит, что система линейных уравнений относительно неизвестных
должны обращаться в 0. Это значит, что система линейных уравнений относительно неизвестных  как известно, для того чтобы однородная система линейных уравнений имела единственное решение, необходимо и достаточно, чтобы ранг матрицы коэффициентов системы был равен числу неизвестных. Таким образом, для того чтобы k элементов n -мерного линейного пространства были линейно независимы, необходимо и достаточ-но, чтобы ранг матрицы, составленной из координат этих векторов, был равен k. Отсюда немедленно следует, что
как известно, для того чтобы однородная система линейных уравнений имела единственное решение, необходимо и достаточно, чтобы ранг матрицы коэффициентов системы был равен числу неизвестных. Таким образом, для того чтобы k элементов n -мерного линейного пространства были линейно независимы, необходимо и достаточ-но, чтобы ранг матрицы, составленной из координат этих векторов, был равен k. Отсюда немедленно следует, что  , то есть максимальное число линейно независимых равно n.
, то есть максимальное число линейно независимых равно n. линейно независимы. Разложим каждый из них по базису
линейно независимы. Разложим каждый из них по базису  . Пусть
. Пусть  – координаты элемента
– координаты элемента  в этом базисе (i =1, 2, …, n). Покажем, что произвольный элемент x из L, имеющий в базисе
в этом базисе (i =1, 2, …, n). Покажем, что произвольный элемент x из L, имеющий в базисе  , может быть представлен в виде линейной комбинации элементов
, может быть представлен в виде линейной комбинации элементов  . Чтобы найти числа
. Чтобы найти числа 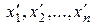 , нужно решить систему линейных уравнений, которая получается, если последнее равенство записать в координатной форме.
, нужно решить систему линейных уравнений, которая получается, если последнее равенство записать в координатной форме. .
. и
и  обозначить через P и
обозначить через P и  , соответственно, торассмотренную систему можно записать в матричной форме следующим образом:
, соответственно, торассмотренную систему можно записать в матричной форме следующим образом: 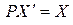 . Приходим к выводу, что если
. Приходим к выводу, что если  в одном базисе и
в одном базисе и  – в другом, то
– в другом, то  , где P – матрица, элементами столбцов которой являются координаты новых базисных элементов в старом базисе.
, где P – матрица, элементами столбцов которой являются координаты новых базисных элементов в старом базисе. и
и  – их базисы, то действие оператора A сводится к умножению слева координатного представления элемента x на матрицу, столбцами которой являются координатные представления образов базисных векторов. Покажем это.
– их базисы, то действие оператора A сводится к умножению слева координатного представления элемента x на матрицу, столбцами которой являются координатные представления образов базисных векторов. Покажем это.
 , а
, а 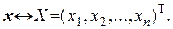 Тогда
Тогда 


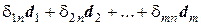 ) =
) = 

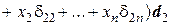 +…+
+…+  .
.
 , то есть Y = AX, где A =
, то есть Y = AX, где A =  ,
,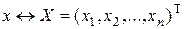 , будем отождествлять элемент x пространства с алгебраическим вектором X, а действие оператора A на x – с умножением вектора X на матрицу A.
, будем отождествлять элемент x пространства с алгебраическим вектором X, а действие оператора A на x – с умножением вектора X на матрицу A. , действительно,
, действительно,  .
.


