
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В процессе обучения математике» на 4 курсеСтр 1 из 11Следующая ⇒
Вопросы к экзамену по спецкурсу «Формирование креативной среды В процессе обучения математике» на 4 курсе Специальности «Физика и математика» 1. Обзор современных технологий обучения (личностно-ориентированные технологии обучения) 2. Обзор современных технологий обучения (технологии развивающего обучения) 3. Обзор современных технологий обучения (эвристическая деятельность в контексте компьютерных технологий) 4. Интегративный подход в обучении математике в средней школе 5. Принцип креативности 6. Виды креативного обучения 7. Уровни и этапы формирования креативности. Оценивание навыков креативности 8. Модель креативной учебной деятельности 9. Универсальная учебная модель формирования базовых поведенческих и интеллектуальных навыков поисковой деятельности 10. Постановка образовательных целей в субъектной форме 11. Постановка развивающих и креативных целей в субъектной форме 12. Постановка воспитательных целей в субъектной форме 13. Полидидактическая технология обучения 14. Модель учебной деятельности на основе метода срезов. Формирование индивидуальной траектории обучения 15. Методика применения метода срезов в контексте сочетания репродуктивной и креативной деятельностей. Применение метода срезов при проблемном изложении теоретического материала 16. Организация этапов поисковой деятельности учащихся 17. Сочетание поисковой деятельности с методом системной интерактивной структуризации учебного материала 18. Обучающие тестовые задания как средство управления процессом решения геометрических задач. Методические приемы обновления системы задач в целях усиления их воспитательного потенциала 19. Методика развития дивергентного мышления учащихся 20. Инновационный школьный электронный учебник (определение, достоинства и недостатки) 21. Формирование интерактивной методики изучения теоретического материала, обучения решению задач 22. Организация мобильного комбинированного урока 23. Применение метода срезов в контексте сочетания репродуктивной и креативной деятельностей 24. Применение метода срезов при проблемном изложении теоретического материала 25. Применение метода срезов при обучении теоретическому материалу через задачи
Интегративный подход в обучении математике в средней школе. Понятие интегративной связи следует рассматривать как новое понятие, отличающееся от понятий внутри- и межпредметной связей. Элементы учебного материала, между которыми устанавливается внутри- или межпредметная связь могут в общей структуре курса находиться на значительном удалении друг от друга. Поэтому не всегда эти связи могут рассматриваться как интегративные. «Интегрировать – объединять части в целое» (словарь Ожегова). Под интегративными связями понимают такие внутри- и межпредметные связи, которые обеспечивают сближение соответствующих элементов и частей учебного материала, объединение их, одновременное и параллельное изучение. В широком смысле под интегративным подходом в обучении понимают систему обучения, построенную на интегративном принципе и включающую в себя все составные части процесса обучения (цели, содержание, средства, методы и формы обучения). Особенно широкими возможностями в обеспечении интегративных качеств обладают методы обучения и соответствующие им методы изложения учебного материала в ИОР. Интеграция (в узком смысле) определяется как систематизация учебного материала, обеспечивающая сближение различных элементов учебного материала в общей его структуре, объединение различных его частей, повышение системных качеств изложения. Возможны следующие виды интегративных учебных материалов: I вид – внутрипредметные связи сильнее межпредметных; II вид – внутри- и межпредметные связи по силе действия примерно одинаковы; III вид – внутрипредметные связи слабее межпредметных. Первые два вида обеспечивают более «плавный» переход от автономных курсов к интегративному, создают условия для сохранения систематического характера учебника. Значительную системообразующую функцию выполняет принцип единства целей обучения. Он связывает все составляющие процесса обучения, содействует его целостности. Однако, он не может в полной мере обеспечить целостность процесса обучения. Наряду с целями, значительной связующей силой обладает предметное (математическое) содержание, его специфика. Учет предметной специфики курса математики в целом и составляющих его учебных тем в силу своей значимости предполагает выделение специального принципа – принципа учета предметной специфики учебного курса. В обеспечении единства процесса обучения значительную роль играет принцип управляемости процесса обучения(формирование внутренней мотивации, стимулирование познавательного интереса, технологичность и диагностичность целей и задач обучения, учет применяемых методов, средств и форм обучения, эффективное использование обратной связи в обучении, ориентация на оперативные, промежуточные и окончательные результаты обучения, самоконтроль и самокоррекция знаний).
Все перечисленные выше признаки и качества процесса обучения присущи и технологии обучения. Именно технология обучения на максимально конкретном уровне решает все эти вопросы. Поэтому принципы единства целей, единства всего процесса обучения, принципы учета предметной специфики учебного материала, принцип управляемости процесса обучения – все они зависят естественным образом от того, насколько технологичным является этот процесс, насколько качественна принятая технология, насколько совместимыми друг с другом оказались модели учебника и процесса обучения. В рамках компьютерно-ориентированной технологии определяется соотношение между компьютерной и некомпьютерными технологиями, определяются конкретные модели ШЭУ, способы реализации СП. Главное состоит в том, что компьютерная технология способна вывести на более высокий уровень технологичности все сопрягаемые с ней технологии. Актуальным является исследование возможностей взаимной дополнительности и сочетания некоторых психолого-дидактических теорий, находящихся как в определенной близости друг к другу, так и являющихся альтернативными. Важно ориентироваться в условиях и границах применения той или иной концепции усвоения и развития, в том, насколько тесно коррелируют между собой психолого-дидактическая концепция и соответствующие ей теоретические разработки системы или технологии обучения. Особенно актуальными в этом плане является рассмотрение с позиции СП основных парадигм (концепций) обучения: ассоциативно-рефлекторной концепции, концепции деятельностного подхода, интериоризаторской концепции обучения, концепции развивающего обучения, гештальт-теории. Теоретический раздел, креативный раздел, тренинг, задания для самоконтроля и внешнего контроля должны дополнять друг друга, строго придерживаясь предназначенных для них функций. Принцип креативности Характеристика принципа креативности. Понятие «креативность» (от лат. creatio– созидание) введено Д.Симпсоном в 1922 г. В психологии существуют различные подходы к понятиям творчества и креативности, к соотношению этих понятий. Креативность рассматривается как интегральная способность к творчеству. По Т.А.Барышевой и Ю.А.Жигалову понятия «творчество» и «креативность» дифференцируются: первое выступает как процесс и результат, второе – как субъективная детерминанта творчества. Значительная часть исследований ведется в контексте понятий «способности» и «одаренность» в их наиболее высоких уровнях проявления (отсюда внимание к школам и классам с математической специализацией, олимпиадам и т.д.). Не меньшая часть психологических исследований исходит из того, что творческий потенциал присущ каждому человеку и степень его проявления и развития зависит как от генетических задатков, так и от свойств среды (В.Н.Дружинин, например, говорит о людях высоко- и низко креативных). По мнению Д.Игнатьева существует миф о том, что креативность – это удел немногих гениев, недоступный большинству людей. На самом деле секрет креативности состоит не столько в создании гениальных глобальных идей, сколько в умении генерировать малые идеи и больше того – в умении малые идеи превращать в большие. Креативность чаще рассматривается не столько как некоторая творческая способность или совокупность таковых, а как способность к творчеству, а эти понятия, хотя близкие, но не идентичные
В структуре креативного потенциала выделяют комплекс способностей успешной деятельности в новых, нестандартных ситуациях. Чаще всего это: а) интуиция и воображение; б) интеллектуальные качества – конвергентное мышление (логическое мышление, ориентирующееся на применение известных подходов решения задач в новых условиях, предполагающее совершение поисковых действий, нахождение единственно правильного решения на основе многих условий), дивергентное мышление (нахождение множества решений на основе однозначно заданных условий); в) компетенции (предметные знания, универсальные способы деятельности, способность к переносу их в новых условиях); г) свойства личности – мотивы, волевые качества, эмоциональность, сопряженные с решением креативных задач. У различных лиц указанные способности развиваются в различной степени, в различных сочетаниях и обусловлено особенностями взаимодействия полушарий головного мозга. Замечено, что как слишком низкая, так и слишком высокая компетентность (в зависимости от уровня проблемы) мешают креативному процессу. Психологической основой креативного обучения могут служить различные концепции и теории развития школьника в процессе обучения (Л.С. Выготского, П.Я. Гальперина, В.В. Давыдова, Л.В. Занкова, А.Н. Леонтьева, Д.Б. Эльконина и др.). Первая методика развития креативного мышления была разработана Р. Крачфиллом. Она исходила из того, что творческие способности могут быть развиты через решение творческих задач. Творческим подходом обладает метод проблемного обучения (М.И.Махмутов), опирающийся на решение специальных познавательных задач – проблем и моделирования проблемных ситуаций. Развивающее обучение по В.В.Давыдову и Л.В.Занкову опирается на учебную деятельность, развивающую теоретическое мышление и личность ученика. В педагогической инженерии Г.П.Щедровицкого и Н.Н.Халаджана акцент в обучении смещается с передачи знаний на организацию образовательной деятельности с целью получения авторизированной учебной продукции. Эвристическое обучение по А.В. Хуторскому, исключая репродуктивные методы, преследует цель не только развить ученика, но и сделать его субъектом, конструктором своего образования. В теории достаточно хорошо известны следующие технологии, ориентированные на развитие креативных качеств: развивающее обучение, технология решения изобретательских задач – ТРИЗ (Г. Альтшулер), технология игрового моделирования, метод проектов, разноуровневое обучение, информационно-коммуникативные технологии, проблемное обучение, диалоговые технологии. Делаются попытки по выделению специальных методов развития креативности (мозговой штурм, метод Дельфи, латеральное мышление по Эдварду де Боно, синектика Уильяма Гордона, «бритва Окинавы» и др.). Выделяют самостоятельные разновидности креативности: личностная и поведенческая (В.Н. Дружинин); интеллектуальная и поведенческая (И.А. Снегова), словесная (вербальная), изобразительная (невербальная), словесно-звуковая (Е.П. Торренс), «специализированная» креативность – способность к творчеству в определенной сфере человеческой деятельности, которая развивается на основе общей креативности.
Развитие при обучении математике это, прежде всего, развитие интеллектуальных способностей. Для методики математики наиболее приемлем подход, в котором считается, что уровни интеллекта и творческих способностей взаимосвязаны, но не совпадают: нет креативов с низким интеллектом, но есть интеллектуалы с низкой креативностью (Е.П.Торренс). Креативность включает в себя не только интеллектуальный потенциал, но и поведенческие навыки – стремление к мотивации, эмоциональному самовыражению, повышению уровня компетентности и т.д. Многие исследователи подчеркивают, что креативность – это обычная, естественная функция психики, а не особое редко встречающееся качество личности. Тем не менее, психологи нередко выделяют креативность как высшую форму мыслительной деятельности (Н.Н Поспелов, Т. Рибо, С.Л. Рубинштейн). В методических исследованиях необходим определенный баланс между этими видами деятельности.
6. Виды креативного обучения. Сравнение традиционного и креативного типов обучения показывает их существенные различия
Креативный тип обучения может быть двух видов: первый, наиболее радикальный – предметное содержание на всем протяжении обучения выступает не как цель, а как средство формирования креативности. Второй, – наиболее приемлемый, совершается в рамках поэтапного эволюционного обновления. В этом подходе задачи выступают в качестве средства развития креативности лишь частично, в этих целях используется только группа первых задач к каждому параграфу. Субъективная новизна этих задач вызывает потребность в креативном подходе; реализация его на первых задачах в опережающем порядке формирует мышление, необходимое для решения следующих более сложных задач.
Рисунок 2.3.Микросреда Рисунок 2.4. Микросреда в виде на графическом материале логико-структурной схемы Пример 2. Как и выше, речь идет о введении группы основных понятий по крупной теме (снова в рамках одной микросреды). Усвоение группы определений проходит успешно, если приводится графическая схема, в концентрированном виде иллюстрирующая связи между понятиями. Например, по теме «Четырехугольники» может быть приведен рисунок 2.4. Пример 3. Лучшему восприятию группы определений способствуют записи определений в виде схемы (рис. 2.5).
Рисунок 2.5. Микросреда на основе записи группы определений в виде cхемы
Рисунок 2.6. Микросреда в виде множества четырехугольников кругами Пример 4. На рисунке 2.6 круг 1 изображает множество всех параллелограммов, круг 2 – множество прямоугольников, круг 3 – множество ромбов. Какие четырехугольники входят в заштрихованную область 4? Пример 5. Укрупненной подаче, относящейся к доказательству теоремы информации (своего рода визуальному ее сворачиванию), способствуют рисунки, на которых показана нумерация шагов доказательства. Например, к доказательству признака параллельности прямых может быть приведен рисунок 2.7.
Рисунок 2.7. Микросреда в виде рисунка с нумерацией на нем шагов доказательства Пример 6. Многоаспектная структуризация текста доказательства с привлечением аудивизуальных средств, представленных на рисунке 2.7, также помогает наглядно отразить структуру доказательства (одновременно на уровне крупных блоков и отдельных шагов). Например, текст доказательства признака параллельности прямых может быть представлен следующим образом.
Теорема (признак параллельности прямых): Если при пересечении двух прямых секущей окажется, что накрест лежащие углы равны, то прямые параллельны. Доказательство I. Вначале применим метод от противного: Пусть при пересечении прямых АС и BD секущей АВ образовались равные накрест лежащие углы (рис. 2.7): Ð BAC = Ð ABD и Ð MAB = Ð NBA. Докажем, что AC || DB. Доказательство проведем методом от противного: 1. Могут ли прямые АС и DB пересекаться? Допустим, что AС ∦ DB. Пусть Е — точка пересечения этих прямых. Какие следствия можно получить из этого допущения? 2. Отложим отрезок АK, равный BE, и соединим точки В и K отрезком. II. Воспользуемся методом равных треугольников: 3. D ВАK = DАВЕ — по двум сторонам и углу между ними. 4. Из равенства этих треугольников следует, что Ð ABK = Ð BAE. 5. Но углу ВАЕ (углу ВАС) равен также угол ABD (по условию). Рисунок 3.7 – К теореме Жордана
Рисунок 3.8 – К проблеме Саккери Рисунок 3.9 – Пример фрактала: кривая Коха Вернемся к проблеме Саккери через 1-2 урока, после изучения свойств параллельных прямых (начинает работать аксиома параллельных) и неожиданно обнаруживаем, что ранее неразрешимая проблема оказывается легко решаемой. Учащиеся проявляют неподдельный интерес, одновременно с этим на доступной, содержательной и весьма поучительной задаче знакомятся с ролью аксиом в геометрии. Пример 3. Фракталы обычно поражают своей красотой, интерес рассмотрения их еще более усиливается, если с ними связать содержательные геометрические задачи. При рассмотрении кривой Коха (построение ее показано на рис. 3.9) возможны задачи на вычисление длины этой кривой при заданной длине исходного отрезка и некоторого числа итераций построений. Непосредственными вычислениями находится длина кривой для n = 2; 3. Обнаруживается закономерность (длина кривой для n = 2 равна Пример 4. Другим примером фракталов может служить группа фракталов, сыгравших в математике значительную роль в обобщении понятия линии (квадрат Серпинского, кривая Пеано и др.). Обратимся к квадрату Серпинского (рис. 3.10): исходный единичный квадрат разбивается на девять квадратов и удаляется квадрат, находящийся в центре; с оставшимися восьмью квадратами повторяются эти же действия и т.д. Процесс продолжается неограниченно. В связи с этим фракталом учащимся полезно предложить следующую задачу: записать последовательность площадей остающихся частей квадрата. С помощью вычислений приходим к следующей последовательности: 1,
Рисунок 3.10 – Пример фрактала: квадрат Серпинского
З) и) к)
Л) м) н)
О) п) р) Рисунок 3.12 – Актуализированное креативное поле задачи 16) площадь прямоугольного треугольника с катетами d 1 и d 2 (рис. 3.12, п); 17) площадь треугольника с основанием АС и высотой, равной BD (рис. 3.12, р). Уровень креативности обучения можно охарактеризовать количеством высказанных идей (широтой охвата креативного поля задачи). Если были высказаны все 17 идей, то уровень креативности обучения максимальный и характеризуется коэффициентом k = 17/17 = 1; если была высказана всего одна идея, то k = 1/17; если идеи сообщались учащимся в готовом виде, то k = 0. Существенным показателем креативности обучения является высказывание блестящей идеи (высказана ли она вообще, в завершении формирования креативного поля, в самом начале, в некоторой его промежуточной части). К сожалению, обычно используется конвергентное мышление: идея высказывается не учащимися, а учителем, или вообще не высказывается, или рассматривается только один способ решения.
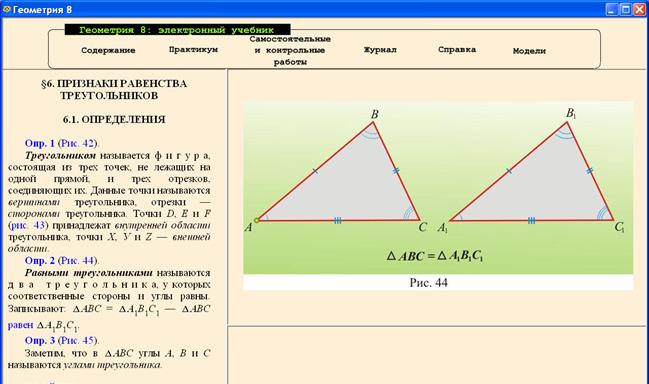
20. Инновационный школьный электронный учебник (определение, достоинства и недостатки) Признаки инновационного ШЭУ: 1) Для представления об ШЭУ как программно-методическом комплексе, интегрирующем программными средствами электронный текст, анимированную графику, модели, тренинг характерно игнорирование дидактического основания интеграции. Инновационный ШЭУ рекомендуется рассматривать как систему локальных ИОС. Эта среда, как и любая среда, должна быть целостной, комплексной, многофункциональной, многовариантной, с параллельными потоками информации, интегративной, представляющей каждому ученику возможность выбора посильного поля деятельности; 2) Инновационный ШЭУ представляется как система, эффективное проектирование и применение которой связывается с полидидактическими технологиями и креативным типом обучения; 3) Инновационный ШЭУ в доступных и активных формах обеспечивает индивидуализацию обучения, учет личностных характеристик при разработке индивидуального подхода и выборе форм общения. Наряду с этим, он учитывает, что субъект успешно развивается и проявляет себя только в коллективе (социальной среде) и поэтому обеспечивает широкое использование коллективных форм познавательной деятельности, применение различных форм и элементов проблемного обучения, ориентирует на совершенствование навыков педагогического общения, мобилизующих творческое мышление обучаемых. Индивидуализация обучения в нем сочетается со стремлением к результативности обучения и равномерному продвижению всех обучаемых в процессе познания; для инновационного ШЭУ интерактивность необходима в избыточной форме, обеспечивающей всестороннее восприятие и осознание информации; 4) Инновационный ШЭУ, тесно коррелируя с действующим учебником на традиционном носителе, не является прямой его электронной копией. ШЭУ по объему учебного материала может быть более кратким, чем традиционный учебник. За счет этого и за счет максимально высокой интерактивности ШЭУ сможет обеспечивать более глубокую проработку основного учебного материала; 5) Программные средства инновационного ШЭУ базируются на использовании систем искусственного интеллекта и имитационных систем, близких к ним. Достоинства ШЭУ 1. Возможность реализации его как определенной системы локальных ИОС, реализации в нем системы образовательных траекторий и микросред, определенной полидидактической технологии, интерактивного взаимодействия между учеником и компонентами учебника. Уровень интерактивности может изменяться от низкого и среднего (перемещение по ссылкам, вызов порции информации того или иного размера) до высокого (использование когнитивной компьютерной графики, самостоятельное тестирование, участие ученика в моделировании процессов, формирование креативных качеств личности). Дополнительные интерактивные возможности появляются за счет объединения в единую систему компьютера, мультимедийного проектора и интерактивной доски (сенсорного экрана, подсоединенного к компьютеру). 2. Новые по сравнению с традиционным учебником мультимедийные средства воздействия на ученика, помогающие быстрее осваивать и лучше запоминать учебный материал. Особенно важным представляется включение в ЭУ анимационных моделей. Определенный эффект дает синхронное звуковое и цветовое сопровождение, дополняющее текст учебника. Еще лучше, если «озвучивание» текста осуществляется не диктором, а учащимися (дополнительная форма интерактивности). 3. Адаптация учебного материала к уровню знаний ученика, что также способствует лучшему восприятию и запоминанию учебной информации. Адаптация основана на возможности выбора траектории обучения. Вместе с этим, адаптации, осуществляемой средствами ШЭУ, легче придать активный характер, стимулирующий ученика на более высокие доступные для него уровни когнитивной и креативной деятельности. 4. Автоматизированный самоконтроль уровня знаний ученика и автоматический выбор в соответствии с уровнем знаний траектории обучения. ШЭУ позволяет поставить на контроль решение всех задач. Такой сплошной контроль проводится, прежде всего, в целях усиления роли самоконтроля, саморефлексии, самокоррекции и самодифференциации, производимыми учеником. 5. Адаптация и оптимизация пользовательского интерфейса с учетом возможностей ученика. Использование текстовой, гипертекстовой, фреймовой структуры учебника. 6. Построение простого и удобного механизма навигации в пределах ЭУ. 7. Удобный поисковый механизм не только в пределах ЭУ, но и вне его (обращаться к внешним источникам информации, Интернет-источникам, интерактивной доске, планшетам). Работа с ШЭУ Вводная часть урока: сообщаются сведения из истории математики, подчеркивается, что признаки равенства треугольников дали исторически первый крупный математический метод доказательства теорем и решения задач, приводятся краткие сведения о Евклиде и его «Началах». В школьном курсе геометрии метод равных треугольников применяется почти «на каждом шагу», поэтому важно каждому ученику овладеть этим методом. Основная часть урока. 1-й срез: обзор основного содержания урока. Сообщается, что на данном уроке познакомимся с тремя определениями, аксиомой, теоремой и ее доказательством. Перелистываем четыре страницы ЭУ (рис. 3.11-3.12) и показываем, с какими определениями будем знакомиться (называем их и попутно показываем соответствующие рисунки). 2-й срез: образовательная микросреда-1 (признаки микросреды – многократная проработка небольшого фрагмента учебного материала, изучение и закрепление определений с многократной обратной связью): просим одного ученика, пользуясь текстом ШЭУ, вслух прочитать тему урока, название первого пункта темы и первое определение; при коллективном участии класса проводим анализ формулировки (какое понятие определяем, через какое понятие); нескольким ученикам дается задание воспроизвести определение 1 по возможности не подглядывая в экранную страницу; предлагаются аналогичные задания в отношении определений 2 и 3; осуществляется тренировка по воспроизведению всех трех определений.
Рисунок 3.11. 1-й срез: обзор основного содержания урока 3-й срез: образовательная микросреда-2 (признаки микросреды – многократная проработка небольшого фрагмента учебного материала, изучение первых двух признаков): один ученик вслух читает по ШЭУ оба признака и воспроизводит их, при необходимости остальные поправляют; после отработки словесных формулировок ученикам предлагается сделать в тетради краткую запись определения равных треугольников и двух признаков равенства. Примерная запись: 1) ∆ АВС = ∆ А 1 В 1 С 1⇔ (АВ = А 1 В 1, ВС=В 1 С 1, АС= А 1 С 1, Ð А = Ð А 1, Ð В = Ð В 1, Ð С = Ð С 1) – определение; 2) (АВ = А 1 В 1, АС= А 1 С 1, Ð А = Ð А 1) Þ ∆ АВС = ∆ А 1 В 1 С 1 – 1-й признак; 3) (АС= А 1 С 1, Ð А = Ð А 1, Ð С = Ð С 1) Þ ∆ АВС = ∆ А 1 В 1 С 1 – 2-й признак. 4-й срез: образовательная микросреда-3 (признаки микросреды – использование интерактивной структуризации учебного материала, изучение доказательства 2-го признака с помощью проблемного метода изложения): инициативу проявляет учитель, он обращает внимание учащихся на замысел доказательства (см. ШЭУ), выясняет с учащимися, почему для доказательства теоремы достаточно доказать равенство АВ = А 1 В 1, что доказательство будет вестись методом от противного, что для этого строится третий треугольник; б) учитель пользуется проблемным методом изложения, руководит пошаговым предъявлением доказательства, каждый шаг доказательства сопровождается синхронной демонстрацией на рисунке.
Рисунок 3.12. 1-й срез: обзор основного содержания урока Теоретического материала Организацию срезов покажем на примере проблемного изложения учебной темы «Уравнения прямой и окружности». Срез 1 (постановка проблем). Проблема-1: Пусть А (х 1; у 1) и В (х 2; у 2) – две точки данной прямой, М (х; у) – произвольная точка этой прямой. Найдем уравнение, связывающее координаты х и у точки М (уравнение прямой). Как вывести уравнение прямой? Какие уравнения прямой существуют? Проблема-2. Пусть точка А (х 1; у 1) – центр окружности, М (х; у) – произвольная точка этой окружности. Представим, что точка М описывает окружность. Координаты точки М будут изменяться, но будут связаны некоторым Равенством, называемым уравнением окружности. Найдем равенство, связывающее координаты х и у точки М. Срезы: 2) решение проблем (уравнения прямой и окружности выводятся, в готовом виде не сообщаются); 3) закрепление теории: воспроизводятся уравнения прямой и окружности, их вывод; 4(креативный задачный раздел: ключевые задачи): Ключевая задача 1: Запишите общее уравнение прямой, проходящей через точки А (–2; 3) и В (1; –5). Для учащихся эта задача первая. Даем им возможность справиться с ней самостоятельно. В случае затруднения организуется поиск решения; Ключевая задача 2:а) Какую линию задает уравнение (х – 3)2 + (у + 2)2 = 4? Постройте эту линию на координатной плоскости; б) какую линию задает уравнение х 2 – 6 х + у 2 = 0? Постройте эту линию на координатной плоскости; в) запишите уравнение окружности с центром А (4; 3), проходящей через начало координат; Срезы: 5(тренировочный задачный раздел): решение задач первых двух уровней сложности; 6 (самоконтроль): решение задач, аналогичных тренировочным задачам; 7 (индивидуальные траектории): решение индивидуальных задач 3-го уровня сложности; 8 (рубежный самоконтроль).
Материалу через задачи Изучение темы «Площади четырехугольников, 8 кл.» можно организовать с помощью следующих этапов и срезов. Срезы 1-3 (теория): определение равновеликих фигур, вывод формул площади параллелограмма, ромба, треугольника, трапеции, понятие о методе площадей. Вопросы для закрепления теории: а) В чем состоит замысел доказательства каждой из теорем? б) Дан D ABC, точка М принадлежит стороне АС, известно что Срез 2 (креативный задачный раздел, решение ключевых задач). Решение задач проводится в поисковом режиме с организацией совместного формирования поведенческих и интеллектуальных навыков: Задачи: 1) Из середины каждой стороны остроугольного треугольника проведены перпендикуляры на две другие стороны. Найдите площадь Q ограниченного ими шестиугольника, если площадь треугольника равна S; 2) диагональ прямоугольной трапеции равна ее боковой стороне. Найдите площадь трапеции, если ее высота равна 4, а боковая сторона 5; 3)в равнобедренной трапеции диагонали перпендикулярны. Найдите площадь трапеции, если ее основания равны 4 и 6; 4) пусть а, b и с – соответственно катеты и гипотенуза прямоугольного треугольника, h – высота, проведенная к гипотенузе. Существует ли треугольник со сторонами h, c + h и a + b? Если да, то установите вид этого треугольника и найдите его площадь; 5) найдите площадь квадрата ABCD, вершины A и D которого лежат на оси абсцисс, а две другие – соответственно на прямых у = х + 1 и у = – 2 х + 3; 6) в прямоугольном треугольнике с катетами а и b и гипотенузой с высота h, проведенная к гипотенузе, находится по формуле h = (ab)/ c. Докажите эту формулу методом площадей; 7) дан остроугольный треугольник с основанием b и высотой h, проведенной к этому основанию. В этот треугольник вписан квадрат, две вершины которого лежат на основании, а две другие – на оставшихся сторонах. Найдите сторону квадрата; 8) существует ли треугольник с высотами, равными 2, 3 и 4? 9) найдите площадь четырехугольника с перпендикулярными диагоналями, равными Срезы: 3 (тренировочный задачный раздел). Решение задач первого и второго уровня сложности, аналогичных предыдущим; 4 (самоконтроль). Задания, аналогичные предыдущим; 5 (индивидуальные траектории). Индивидуальные задания третьего уровня сложности; 6 (задания для рубежного самоконтроля).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 231; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.175.113 (0.123 с.) |



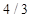 , для n = 3 равна
, для n = 3 равна 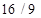 ). Высказывается предположение, что для n = 4 длина равна
). Высказывается предположение, что для n = 4 длина равна 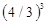 . Это предположение подтверждается непосредственными вычислениями. Индуктивным путем получается формула ln =
. Это предположение подтверждается непосредственными вычислениями. Индуктивным путем получается формула ln = 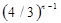 . Обоснование формулы в общем виде может быть рассмотрено при ознакомлении в алгебре с геометрической прогрессией.
. Обоснование формулы в общем виде может быть рассмотрено при ознакомлении в алгебре с геометрической прогрессией.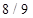 ,
, 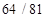 ,…,
,…, 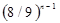 ,… Видно, что при n →
,… Видно, что при n → 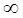 «остаточная» площадь квадрата Sn → 0, что характерно для линии («дырявый» квадрат превращается в своеобразную геометрическую «паутину»).
«остаточная» площадь квадрата Sn → 0, что характерно для линии («дырявый» квадрат превращается в своеобразную геометрическую «паутину»).


 . Докажите, что ВМ является медианой данного треугольника. в) Точка О является точкой пересечения двух медиан D АВС. Докажите, что
. Докажите, что ВМ является медианой данного треугольника. в) Точка О является точкой пересечения двух медиан D АВС. Докажите, что  ;
; и
и  ; 10) докажите, что биссектриса треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам.
; 10) докажите, что биссектриса треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам.


