
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лема про три границі. Граничні переходи у нерівностях.
Теорема. 1. Нехай Якщо А<В, то 2. Hexaй числові послідовності Доведення. 2)
Нехай Отже, Наслідки Нехай 1. Якщо 2. Якщо 3. Якщо 4. Якщо Приклад. Довести Доведення.
За лемою про три границі 4. Топологічні добутки. Послідовності в Rn. Повернемося до послідовностей у загальному вигляді. Розглянемо ситуацію у метричних просторах, хоча усе зазначене нижче справедливе і у випадку довільних топологічних просторів. Нехай Приклад. На На Теорема. Для того, щоб послідовність ( Доведення. Достатність випливає із збіжності
Зауваження. Теорема справедлива для добутку n метричних просторів
Приклад. Якщо Практичне заняття №9 Тема: Границя послідовності. Необхідні відомості: 1. Визначення границі послідовності. 2. Властивості границь послідовностей. 3. Граничні переходи в нерівностях. 4. Властивості монотонних послідовностей.
Задачі: 1.1.Довести 1.2.Довести, що послідовність 1.3.Довести збіжність послідовностей 2. Використовуючи властивості граничних переходів розв’язати наступні задачі: 2.1.Довести 2.2.Знайти 2.3.Нехай 2.4.Розв’язати рівняння 2.5.Довести нерівність
Завдання для самостійної роботи. Довести: 1. 4. 7. 9. Знайти 10. Нехай
11. Довести збіжність послідовності 12. Довести збіжність послідовності 13. Довести, що послідовність Довести, що послідовності мають границю: 14. 15. 16. 17.Знайти границю послідовності 18.Знайти значення виразу 19.Нехай 20.Довести збіжність та знайти границю 21.Довести, що монотонна послідовність буде збіжною, якщо збігається деяка її підпослідовність. 22.Довести, що якщо 23.Довести, що якщо послідовність 24.Якщо 25.Довести
Практичне заняття №10 Тема: Обчислення границі послідовності. Число е. Необхідні відомості: 1. Властивості границі суми, добутку та ділення. 2. Число е. 3. Границя в прямому добутку метричних просторів. Задачі 1. Знайти границю: 1.1. 1.2. 1.3.
1.4. 1.5. 1.6. 2. Знайти границі, використовуючи число е: 2.1. 2.2. 3. Знайти границі послідовностей 3.1. 3.2. Завдання для самостійної роботи: Довести: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. При яких а послідовність 16. 17. 18. 19. 20. 21. Нехай 22. 23. 24. 25. Лекція №11 Границя функції. Означення по Коші і Гейне. Чудові границі. Границя функції. Означення по Гейне і Коші. Нехай Означення 1 (топологічне). Точка у0 є F - границя функції Приклад. 1. Якщо Х=R, A=N, 2. Нехай X - метризований простір, тоді означення 1 буде еквівалентне означенню границі функції по Гейне. Означення 2. Точка у0 Доведемо еквівалентність означень. Означення 2 випливає з означення 1 (навіть якщо X просто топологічний простір). Дійсно, нехай означення 1 виконується. Якщо
Доведемо, що означення 1 випливає з означення 2. Нехай виконується означення 2. Припустимо, що означення 1 не виконується, тобто Розглянемо ситуацію, коли X і F - метричні простори з метриками Означення (по Коші). Точка у0
Означення по Коші та по Гейне еквівалентні (у зв’язку з вище доведеним). Приклад. 1. E=F=R
Означення.
Позначимо Означення.
Позначимо З означень границі та границь справа та зліва випливає, що границя існує тоді і тільки тоді, коли існують границі з права та зліва, що рівні між собою. Крім того, множину А, нижче, не будемо вказувати, якщо вона є зрозумілою з контексту або співпадає з областю визначення функції. 2. Довести Знайдемо Припустимо, що
3. Функція 4. Число y0
Зазначимо, що границя не залежить від того по якому шляху рухається 5. Нехай Е=R2, a F=
Розглянемо границю При При При Тобто в залежності від того по якому шляху точка (
2. Чудові границі: 1. Перша чудова границя: Доведення. Оскільки вираз
S∆AOC= SсектораAOC= S∆AOB= Отримали:
Тоді за лемою про три границі 2. Друга чудова границя: Доведення. Покажемо за Гейне: Нехай
Звідси, Наведемо ще деякі означення границь. Означення границь для випадку Е = F = R1: 1. 2. 3. Зауваження: Самостійно сформулювати означення границь для випадку Е= F= R1 при
Лекція №12 Властивості границь. Неперервність. Розриви функцій 1. Властивості границь функцій. Теорема 1. Нехай (Довести самостійно, подібно аналогічній властивості для послідовностей). Теорема 2. Нехай Доведення. Візьмемо в якості V (згідно означення 1 лекції №11) кулю з центром у0 довільного радіуса R, тоді згідно з означенням границі існує окіл U точки
Приклад. Теорема 3. (про границю складної функції). Нехай Доведення. Для будь-якого окола V точки z0, Розглянемо тепер більш конкретну ситуацію. Теорема 4. Нехай
мають скінчені границі при х Доведення. Використаємо означення Гейне: для довільної послідовності Означення. Якщо Кінцева сума нескінченно малих - нескінченно мала; добуток нескінченно малої на обмежену функцію - нескінченно мала (за властивостями границь). Означення. Дві нескінченно малі при Наприклад, sinх~х при Означення.
Наприклад. g( Теорема 5. Нехай Якщо
то існує границя g(x) при Доведення, як і властивість 4, за допомогою означення Гейне, та відповідної властивості послідовності. Теорема 6. Нехай Доведення провести самостійно. 2. Неперервність. Розриви. Враховуючи означення неперервності (див. лекцію №7) і границі функції можна сформулювати висновок. Означення. Функція З властивостей границь випливає, що всі ці властивості виконуються для неперервних функцій в точці або на всій множині X. Зупинимось на властивості 4. Якщо Нехай
Приклад. З властивостей неперервних функцій та неперервності функцій 1. 2. Зупинимося на функціях
по кожній змінній неперервна в (0,0), але границі не має, тобто неперервною не є. Означення. Якщо рівність Нехай 1. 2. Розриви 1-го роду зліва (зправa). Якщо 3. Розриви 2-го роду зліва (зправa). Якщо Теорема. Монотонна функція має розриви тільки 1-го роду, причому не більше ніж злічене число. Доведення спирається на теорему про границю монотонної функції. Довести самостійно.
Практичне заняття №11 Тема: Границя функції Основні відомості: 1. Визначення границі функції по Коші та Гейне.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 619; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.71.237 (0.212 с.) |
 і
і  - збіжні числові послідовності з границями А і В відповідно.
- збіжні числові послідовності з границями А і В відповідно. .
. такі, що
такі, що  . Якщо
. Якщо  мають одну границю
мають одну границю 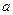 , то
, то 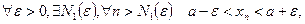
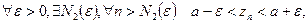
 , тоді
, тоді 
 тобто
тобто  n}.
n}. =А
=А 

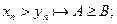




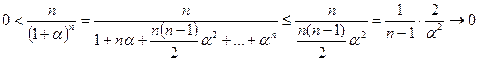 .
.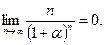
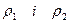 - метрики в Е1 і Е2. На множині Е1
- метрики в Е1 і Е2. На множині Е1  Е2 за допомогою формули
Е2 за допомогою формули  можна ввести метрику.
можна ввести метрику. маємо:
маємо: 
 маємо:
маємо: 
 1,
1, 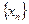 була збіжною в Е1 до
була збіжною в Е1 до  , а також збіжність (
, а також збіжність ( (згідно з означенням границі).
(згідно з означенням границі).
 і нерівності
і нерівності
 .
. збігається до точки (
збігається до точки ( в
в  .
.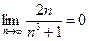 ;
;  ;
; 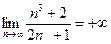


 (використовувати критерій Коші).
(використовувати критерій Коші). (використовувати нерівність Бернуллі);
(використовувати нерівність Бернуллі);  (використовувати оцінку за допомогою середнього арифметичного).
(використовувати оцінку за допомогою середнього арифметичного). (оцінити знизу та зверху дріб).
(оцінити знизу та зверху дріб). . Довести, що
. Довести, що 
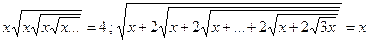

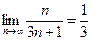 2.
2.  3.
3. 
 5.
5.  6.
6. 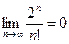
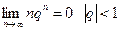 8. Знайти
8. Знайти 
 ,
, 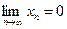 та
та  для будь-якого
для будь-якого  . Довести, що
. Довести, що 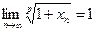
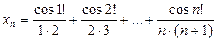
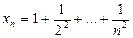 (використовувати
(використовувати 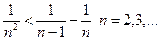 ).
). розбігається.
розбігається.




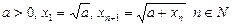 . Довести, що існує
. Довести, що існує  і знайти його.
і знайти його.
 , то
, то 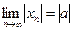
 не обмежена, то існує підпослідовність
не обмежена, то існує підпослідовність  така, що
така, що  .
. , то
, то  . Довести за допомогою критерію Коші.
. Довести за допомогою критерію Коші. .
. ;
;  .
.
 ;
; 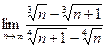 ;
;

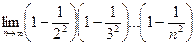 (звернути добуток)
(звернути добуток)
 ;
; 
 .
.









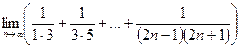

 ,
,  0.
0.

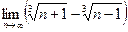
 - n має границю? Чому вона дорівнює?
- n має границю? Чому вона дорівнює?




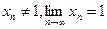 . Знайти
. Знайти 




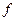 : Х
: Х  F, де X, F - топологічні простори, а
F, де X, F - топологічні простори, а  і точка х0 - гранична для А.
і точка х0 - гранична для А.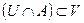 . Позначаємо: у0=
. Позначаємо: у0= 
 ,
,  - границя послідовності
- границя послідовності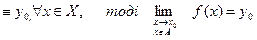 - для будь-якого
- для будь-якого  і А
і А 
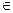 F - границя функції
F - границя функції 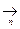
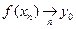 в F.
в F. , то для U з означення 1
, то для U з означення 1 , тобто
, тобто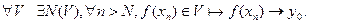
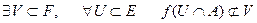 . Візьмемо за U шари
. Візьмемо за U шари  , тоді
, тоді 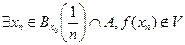 (перетин не порожній, так як точка х0 гранична для А). Одержали суперечність: хn
(перетин не порожній, так як точка х0 гранична для А). Одержали суперечність: хn  , яка і доводить твердження.
, яка і доводить твердження. і
і  відповідно. Означення 1 у цьому випадку прийме вигляд:
відповідно. Означення 1 у цьому випадку прийме вигляд: таке що
таке що  для якого виконується умова
для якого виконується умова  виконується нерівність
виконується нерівність .
.
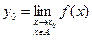 , означає, що
, означає, що 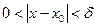 , виконується нерівність
, виконується нерівність  .
. виконується нерівність
виконується нерівність 
 виконується нерівність
виконується нерівність 

 (для довільного
(для довільного  ).
). , тоді
, тоді  або
або  і
і  . Отже
. Отже . Якщо
. Якщо 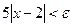 , то
, то  . Візьмемо
. Візьмемо  , тоді якщо
, тоді якщо  , отже означення виконується, що і треба було довести.
, отже означення виконується, що і треба було довести. не має границі при
не має границі при  . Дійсно якщо розглянути послідовності
. Дійсно якщо розглянути послідовності  , то обидві послідовності збігаються до 0, однак
, то обидві послідовності збігаються до 0, однак  отже означення Гейне не виконується.
отже означення Гейне не виконується.


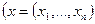 ,
, 

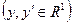
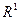 - границя
- границя  по множині
по множині 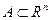 , якщо
, якщо 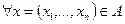 , такого, що
, такого, що  виконується
виконується .
.

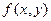 при (
при (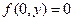 і має границю 0 при (0,
і має границю 0 при (0,  і має границю 0 при (
і має границю 0 при ( і має границю
і має границю 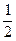 при (
при (

 парний, то можливо припустити що
парний, то можливо припустити що  S∆AOC<SсектораAOC<S∆AOB,
S∆AOC<SсектораAOC<S∆AOB,
 , (коло R=1),
, (коло R=1),
 поділив нерівність на sin
поділив нерівність на sin  або
або 
 (Довести самостійно з означення).
(Довести самостійно з означення). .
.
 . Для кожного n
. Для кожного n  kn
kn 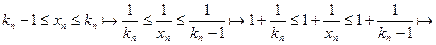

 (як підпослідовність
(як підпослідовність 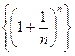 ) і
) і 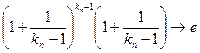
 , тобто за Гейне
, тобто за Гейне 
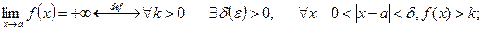


 і
і 
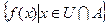 - обмежена.
- обмежена.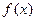 має границю, то
має границю, то  .
. в точці x0 має границю z0.
в точці x0 має границю z0. , існує окіл
, існує окіл  , що
, що  . Для
. Для  окіл
окіл  , що
, що 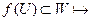 для будь-якого околу
для будь-якого околу 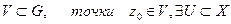 окіл х0 такий, що
окіл х0 такий, що  , тобто означення границі виконується.
, тобто означення границі виконується.
 В,
В,  ,
, 

 , маємо
, маємо  за властивостями числових послідовностей, що і потрібно було довести. (Аналогічно доводяться і інші твердження).
за властивостями числових послідовностей, що і потрібно було довести. (Аналогічно доводяться і інші твердження). нескінченно мала величина при
нескінченно мала величина при  , якщо
, якщо 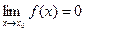

 .
. - нескінченно мала більш високого порядку ніж
- нескінченно мала більш високого порядку ніж 
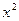 ,
, 
 , тоді
, тоді 
 та існують
та існують

 , а
, а  гранична для Е), необхідно і достатньо, щоб
гранична для Е), необхідно і достатньо, щоб  (
(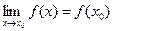
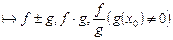 - неперервні в
- неперервні в  - топологічні простори. Якщо
- топологічні простори. Якщо  , то складна функція
, то складна функція  , маємо
, маємо
 неперервна в
неперервна в  неперервна в усіх точках, в яких знаменник не перетворюється в 0.
неперервна в усіх точках, в яких знаменник не перетворюється в 0. неперервна в
неперервна в  - неперервне за виключенням точок у яких знаменник перетворюється в 0 (Q(
- неперервне за виключенням точок у яких знаменник перетворюється в 0 (Q( ) – многочлен двох змінних).
) – многочлен двох змінних).
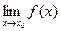 порушується, то говорять про розрив в точці
порушується, то говорять про розрив в точці  =
=  існує, але
існує, але 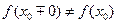
 , або не існує, або нескінченний.
, або не існує, або нескінченний.


