
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 7: ряды предпочтительных чиселСодержание книги
Поиск на нашем сайте
Основой нормализации являются ряды чисел, подчиняющихся определенным закономерностям. В арифметических рядах каждый член образуется прибавлением к предыдущему члену постоянного числа (разность прогрессии) τ. Величина любого члена ряда ак = а0 + kτ, где k — порядковый номер члена; а0 — первый член ряда, которому присваивается нулевой номер. На рис. 11, а показаны арифметические ряды с а0 = 10, τ = 10 ÷ 1 в диапазоне k = 0 ÷ 30. При τ = 5 арифметический ряд в диапазоне наиболее употребительных в машиностроении диаметров D = 10 ¸ 100 мм следующий: 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70... 100.
Рисунок 11 – Арифметические (а) и геометрические (б) ряды; k – порядковый номер члена ряда
Арифметические ряды отличаются относительной неравномерностью. Их верхние области больше насыщены градациями размеров, а нижние меньше. Отношение каждого члена ряда к предыдущему имеет большую величину для первых членов ряда и резко уменьшается в верхних областях ряда. Неравномерность можно отчасти исправить изменением величины t для различных областей ряда. Так, для приведенного выше ряда в диапазонах D < 20, D = 20 ¸ 50 и D = 50 ¸100 мм можно принять соответственно t = 2,5, t = 5 и t= 10. Тогда получается ряд 10; 12,5; 15; 17,5; 20; 25; 30; 35; 40; 45; 50; 60; 70; 80; 90; 100 с более равномерной градацией размеров. В рядах, построенных по принципу геометрической прогрессии, каждый член ряда получается умножением предыдущего члена на постоянную величину j (знаменатель прогрессии). Основные ряды. ГОСТ 8032 - 56 устанавливает пять рядов предпочтительных чисел со знаменателем прогрессии
Таблица 2 – Обозначение рядов
Величина любого члена ряда аk = a0 jkгде k— порядковый номер члена; a0 - первый член ряда, которому присваивают нулевой номер. С уменьшением j интервалы между членами ряда уменьшаются, число членов ряда возрастает; ряд получается более дробным (рис. 11, б). Основные ряды предпочтительных чисел в диапазоне 1 - 10:
большим округлением чисел по сравнению с основными. В отличие от основных ряды нормальных размеров обозначают буквой а:
ГОСТ 6636-69 охватывает линейные размеры в интервале 0,001 — 20000 мм. Применение тестированных линейных размеров целесообразно для поверхностей, подвергаемых точной механической обработке, особенно для диаметров посадочных соединений, что способствует нормализации режущего, контрольного и мерительного инструмента и облегчает настройку станков. Главный экономический выигрыш получается при сокращении числа членов рядов, т. е. при применении в каждом отдельном случае наиболее низкого ряда, обеспечивающего нужный диапазон размеров. Меньшее значение имеют нормальные размеры для поверхностей, не нуждающихся в точной координации. На основании нормальных линейных размеров устанавливают ряды диаметров проволоки, прутков, толщины листового проката, линейных размеров сечений фасонного проката. Применять нормализованные ряды для осевых размеров и для размеров необрабатываемых поверхностей (литье, штамповка) нерационально. В таких случаях даже частичная нормализация размеров, не давая никаких реальных преимуществ, только усложняет процесс проектирования и изготовления деталей, Ряды предпочтительных чисел в конструировании. Значение рядов предпочтительных чисел для конструирования не следует переоценивать. Некоторые конструкторы считают необходимым применять ряды предпочтительных чисел для нормализации и для всех областей конструирования. Это неверно. Ряды предпочтительных чисел целесообразно использовать в случаях, когда требуется создавать ряд градаций какого-либо параметра с равномерной насыщенностью градаций во всех частях ряда (например, передаточных отношений в коробках передач и подач металлорежущих станков). Однако равномерное распределение градаций не всегда является наиболее рациональным. Правильнее при нормировании технических параметров исходить из плотности распределения применяемости данного параметра.
Рисунок 12 – Применяемость модулей зубьев
В качестве примера на рис. 12 приведен график применяемости модулей зубьев в общем машиностроении. Как видно, 90% всех применяемых колес имеют модуль в пределах т = 1 ¸ 5. Максимум применяемости приходится на колеса с модулем 2 - 3. В данном случае целесообразно увеличить число градаций в области наибольшей применяемости и сократить число градаций для редко применяемых модулей. В других отраслях машиностроения (приборостроение, тяжелое машиностроение) соотношения могут быть иными. В каждой отрасли можно установить плотность распределения применяемости и соответственно выбрать градации стандартных модулей. Такой же дифференцированный подход в сущности необходим и для других нормируемых в машиностроении параметров (размеры посадочных диаметров, резьб и др.). Ряды предпочтительных чисел неприменимы для создания унифицированных рядов машин с повторяющимися рабочими органами. Параметры унифицированных рядов складываются по другим законам, зависящим от реальных возможностей сочетания унифицированных органов и условий технической применяемости членов ряда, и не могут уложиться в геометрическую прогрессию. Параметрические ряды необходимо строить с учетом применяемости различных категорий машин, степени их гибкости и т. д. Формальное применение геометрических прогрессий может привести к большим ошибкам. Неприменимы ряды предпочтительных чисел и для: определения параметров прогрессивно развиваемых и модернизируемых машин, параметры которых на каждой стадии зависят от технических возможностей и потребностей соответствующих отраслей народного хозяйства. Так, мощность тепловых машин зависит от их начальных параметров (давления и температуры) и частоты вращения. Ни один из этих параметров невозможно произвольно увеличить. В некоторых случаях они имеют оптимальное значение (например, степень сжатия в газовых турбинах), изменение которого ухудшает показатели машины. Увеличение температуры и частоты вращения возможно только на базе технических усовершенствований (повышения жаропрочности материалов, улучшения охлаждения термически напряженных деталей). Результаты этих поисковых работ невозможно уложить в ряды предпочтительных чисел. Общий вывод состоит в том, что параметры нормализуемых элементов следует выбирать не на основе априорных закономерностей, а исходя из конкретных условий их применяемости.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 922; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


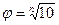 . Степени n корня приняты равными 5, 10, 20, 40 и 80. Эти числа вместе с буквой R составляют обозначение, ряда (таблица 2).
. Степени n корня приняты равными 5, 10, 20, 40 и 80. Эти числа вместе с буквой R составляют обозначение, ряда (таблица 2).








