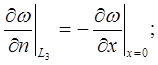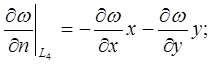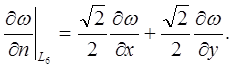Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв’язок деяких задач математичної фізики методом поділення змінних.Стр 1 из 4Следующая ⇒
Розв’язок деяких задач математичної фізики методом поділення змінних.
Методичні вказівки до виконання типового завдання з дисципліни “Рівняння математичної фізики”.
Виконання цього типового завдання передбачається при вивченні дисципліни “Рівняння математичної фізики”. Мета завдання: виробити навички практичного використання математичного апарату у розв’язку задач з реальним фізичним змістом. Типове завдання має три задачі: поширення тепла в стержні, повздовжні коливання струни та стаціонарне розподілення температури у платівці. Їх розв’язок ведеться одним з методів математичної фізики – методом поділення змінних, або як його інакше називають – методом Фур’є.
Виведення рівняння теплопровідності. Розглянемо однорідний стержень довжиною L при таких припущеннях: 1) стержень зроблений з однорідного матеріалу (мал.1.1);
0
мал.1.1
2) бічна поверхня стержня теплозольована (тепло може розповсюджуватись тільки вздовж осі OX); 3) стержень тонкий, тобто температура всіх точок у кожному поперечному перерізі стержня постійна і змінюється тільки від перерізу до перерізу. Якщо розглянемо частину стержня на відрізку
З іншого боку, якщо ввести позначення:
і скористатися формулою обчислення тепла на відрізку
Тоді закон збереження енергії (1.1) можна записати в математичній формі:
де
Задача полягає у тому, що треба записати рівняння (1.2) у формі, в якій нема інтегралів. Для розв’язку цієї задачі треба вжити теорему про середнє значення: якщо функція
В результаті одержимо наступне рівняння
або, якщо поділити на
Спрямуємо
де
Розглянемо випадок, коли бічна поверхня стержня не теплоізольована. Відомо, що величина теплового потоку через бічну поверхню стержня в цьому випадку пропорційна різниці між температурою стержня і температурою навколишнього середовища, яка підтримується постійною і дорівнює нулю. У цьому випадку закон збереження кількості тепла призводить до рівняння:
де
Перетворення задачі з неоднорідними граничними умовами Метод поділення змінних. (Метод Фур’є). Сутність методу – розклад шуканого розв’язку на добуток найпростіших компонент. Метод поділення змінних вживається у таких випадках: 1.Рівняння лінійне й однорідне (не обов’язково з постійними коефіцієнтами). 2.Граничні умови задаються у вигляді:
де
Загальні принципи метода поділення змінних. Для найпростішого рівняння з частинними похідними поділення змінних – це пошук розв’язку у вигляді:
де X(x) – функція, залежна від змінної х; T(t) – функція, залежна від змінної t. Необхідно знайти нескінченне число таких розв’язків рівняння з частинними похідними, які задовольняють граничним умовам. Ці найпростіші функції
Розв’язок задачі U(x,t) знаходиться у вигляді лінійної комбінації фундаментальних розв’язків
яка задовольняє початковим умовам. І оскільки ця сума задовольняє рівнянню і граничним умовам, вона є розв’язком вихідної задачі.
Пошук розв’язку, який задовольняє рівнянню, граничним та початковим умовам. Треба знайти суму фундаментальних розв’язків
з такими коефіцієнтами Ck, щоб функція U(x,t) задовольняла початковій умові
Поширення тепла у стержні. Задача. Нехай на лівому кінці стержня з теплоізольованою бічною поверхнею підтримується постійна температура, яка дорівнює 2 одиницям, а на правому кінці задана теплова течія, яка дорівнює 5. Початковий розподіл температури показаний на малюнку 4.1. Проведемо дослідження з часом зміни цього розподілу.
0
Мал. 4.1 З малюнка легко вивести аналітичну форму функції U(x,0)=f(x), яка буде
Враховуючи, що
рівняння (4.2) та умови (4.1) і (4.3) перепишемо у вигляді
Оскільки у даній задачі граничні умови неоднорідні, то безпосередньо вживати метод поділення змінних не можна. Неоднорідні граничні умови потрібно перетворити в однорідні. Для цього будемо шукати розв’язок задачі у формі
де
Підставимо (4.7) в (4.8), отримаємо
Тоді співвідношення (4.8) приймає вигляд:
або
Сформулюємо вихідну задачу відносно функції
Далі розв’язуємо рівняння методом Фур’є, тобто розв’язок шукаємо у формі
Розв’язок (4.14) підставляємо у рівняння (4.11).
Поділимо праву та ліву частини рівності на
Остання рівність можлива лише у тому випадку, коли обидві частини не залежать від
Розв’яжемо ці рівняння і підставимо в (4.14), тоді будемо мати
де Отже отримали загальний розв’язок рівняння (4.11). Для знаходження частинного розв’язку з граничних та початкових умов визначимо константи. З граничних умов задачі Штурма-Ліувілля маємо
отже
Власними функціями є
Оскільки одержане число
Цей розв’язок рівняння (4.11) задовольняє граничним умовам (4.12) і для кожного значення Тому слід надати константі індекс
Сума розв’язків (4.19) буде також розв’язком рівняння (4.11), тому що розв’язки складають лінійно-незалежну фундаментальну систему. Таким чином
Для визначення довільної константи
Остання формула показує, що константи
Підставимо вираз (4.15) для функції
Виконав необхідні обчислення, дістанемо
Підставимо (4.21) в (4.20) і, враховуючи рівність (4.9), запишемо остаточний розв’язок задачі:
Нехай
Мал.4.2
З цих вислідів видно, що наявність течії на одному кінці стержня і постійної додатної температури на другому, призводять до явища, коли стержень охолоджується з часом дуже повільно.
Будемо розглядати рівняння
де
Рівняння (5.1) відповідно з визначенням операторів div і grad:
можна записати
Розберемо виведення рівняння (5.1) на прикладі малих поперечних коливань струни. Струною називається натягнута нитка, яка не чинить опір згину. Нехай в площині
Оскільки струна не чинить опору згину, то її натяг
Мал. 5.1.
Будь яка ділянка струни
Таким чином, відповідно закону Гука, величина натягу Складемо рівняння руху струни. На її елемент
Але в рамках нашого наближення
тому з (5.3) маємо
відкіля при
Це й є рівняння поперечних коливань струни. При Якщо щільність
де
Рівняння (5.5) будемо також називати одномірним хвильовим рівнянням.
Метод граничних елементів. Для розв’язку ряда задач достатньо визначити шукані величини тільки на межі досліджуваної області, що знижує розмірність розглядуваних задач.
Одним з найбільш широко використаних чисельних методів, що дозволяють вирішити дану проблему, є МГЕ, суть якого полягає у слідуючому. Нехай U0 – точний розв’язок рівняння Лапласа на області
що задовольняє граничним умовам.
( Точний розв’язок U0 може бути знайдено тільки для небагатьох (до того ж простих) випадків, тому, як правило, розв’язок треба апроксимувати. Отже, отримаємо наближений вираз для функції U, тобто розв’язок, підстановка якого в (2.1) і (2.2) порушить указані рівності:
де Таким чином, для розглядуваної області
Тепер головне завдання – зробити ці помилки якнайменшими як у розглядуваній області, так і на межі. Для цього розподілимо функцію помилок наступним чином згідно з [1]:
де
Співвідношення (2.5) можна записати в іншому вигляді, використовуючи вираз (2.4):
Вагова функція
на всій площині
Інтегруючи співвідношення (2.7) два рази за частинами та враховуючи (2.8), отримаємо
Тут Якщо контур
причому на кожному елементі Ui і qj вважаємо постійними
В якості вагової функції розглянемо фундаментальний розв’язок рівняння Лапласа
Оскільки рівняння (2.10) однорідне, коефіцієнт перед логарифмом можна відкинути. Координати джерела Координати джерела можна обчислити за формулами
Підставляючи вагову функцію (2.11) у (2.10), отримаємо систему лінійних алгебраїчних рівнянь, коефіцієнти якої є криволінійні інтеграли першого роду, обчислювані для кожного елемента. Для обчислення значення U у внутрішній точці i області
яке зв’язує значення функції U в точці i зі значенням q і U на межі У формулі (2.13) Примітка. Для визначення
1. Коли нормаль направлена до центру кола, рівняння кола
знаходимо
складемо допоміжну функцію
Тоді
2. Якщо нормаль направлена від центру, рівняння кола запишеться
Подальші міркування аналогічні наведеним у п. 1. Отримаємо
Приклад 2.1. Розглянемо задачу теплопровідності для контура (мал. 2.1), де на сторонах L1, L2, L4, L5 – задана температура, а на сторонах L3, L6 – задано тепловий потік.
Математична формуліровка задачі має вигляд
Тоді за контур
Враховуючи
отримаємо
Розв’язок деяких задач математичної фізики методом поділення змінних.
Методичні вказівки до виконання типового завдання з дисципліни “Рівняння математичної фізики”.
Виконання цього типового завдання передбачається при вивченні дисципліни “Рівняння математичної фізики”. Мета завдання: виробити навички практичного використання математичного апарату у розв’язку задач з реальним фізичним змістом. Типове завдання має три задачі: поширення тепла в стержні, повздовжні коливання струни та стаціонарне розподілення температури у платівці. Їх розв’язок ведеться одним з методів математичної фізики – методом поділення змінних, або як його інакше називають – методом Фур’є.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.108.9 (0.335 с.) |






 і скористуємось законом збереження тепла, тобто загальна кількість тепла на відрізку
і скористуємось законом збереження тепла, тобто загальна кількість тепла на відрізку  дорівнює сумі кількості тепла, що проходить через межі, й тепло створене всередині відрізку, тобто:
дорівнює сумі кількості тепла, що проходить через межі, й тепло створене всередині відрізку, тобто: (1.1)
(1.1) – температура стержня,
– температура стержня,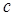 - питома теплоємність матеріалу (означає здібність матеріалу запасати тепло),
- питома теплоємність матеріалу (означає здібність матеріалу запасати тепло), -густина матеріалу,
-густина матеріалу, – площа поперечного перерізу стержня
– площа поперечного перерізу стержня стержня, то маємо
стержня, то маємо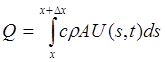 .
.
 (1.2)
(1.2) – теплопровідність матеріалу (здатність матеріалу проводити тепло),
– теплопровідність матеріалу (здатність матеріалу проводити тепло), – об’ємна потужність зовнішнього джерела тепла.
– об’ємна потужність зовнішнього джерела тепла. неперервна на відрізку
неперервна на відрізку  , то існує не більш, як одна точка
, то існує не більш, як одна точка  така, що
така, що .
.
 , то
, то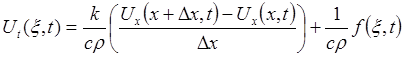 .
. до
до  і одержимо шукане рівняння:
і одержимо шукане рівняння: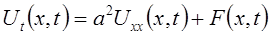 , (1.3)
, (1.3) - коефіцієнт теплопровідності,
- коефіцієнт теплопровідності,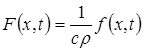 – щільність джерела тепла.
– щільність джерела тепла. , (1.4)
, (1.4) - коефіцієнт пропорційності для потоку через бічну поверхню.
- коефіцієнт пропорційності для потоку через бічну поверхню.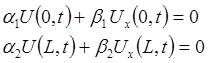 ,
,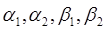 – константи (такі граничні умови називаються лінійними однорідними).
– константи (такі граничні умови називаються лінійними однорідними).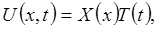
 називаються фундаментальними розв’язками.
називаються фундаментальними розв’язками. тобто вислідна суми
тобто вислідна суми
 (3.7)
(3.7)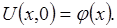












 (4.1)
(4.1) ;
;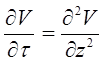 (4.5)
(4.5) (4.6)
(4.6)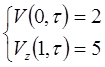 (4.7)
(4.7) (4.8)
(4.8) - функція, яка задовольняє однорідним граничним умовам, аналогічним (4.7);
- функція, яка задовольняє однорідним граничним умовам, аналогічним (4.7); - лінійна функція, яка задовольняє неоднорідним граничним умовам.
- лінійна функція, яка задовольняє неоднорідним граничним умовам.
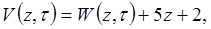 (4.9)
(4.9)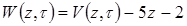 . (4.10)
. (4.10)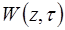 . Для цього (4.9) підставимо в (4.5). Отже задача буде
. Для цього (4.9) підставимо в (4.5). Отже задача буде (4.11)
(4.11) (4.12)
(4.12) (4.13)
(4.13) (4.14)
(4.14)
 , отримаємо
, отримаємо (4.15)
(4.15) і
і  ,тобто є постійними величинами. Позначимо її через
,тобто є постійними величинами. Позначимо її через 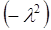 . Тоді з рівності (4.15) одержимо два звичайних диференціальних рівняння
. Тоді з рівності (4.15) одержимо два звичайних диференціальних рівняння (4.16)
(4.16) (4.17)
(4.17) (4.18)
(4.18)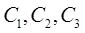 - довільні сталі.
- довільні сталі.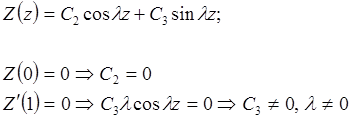

 .
. залежить від
залежить від  , яке змінюється до нескінченності, то кожному значенню
, яке змінюється до нескінченності, то кожному значенню  буде відповідати розв’язок
буде відповідати розв’язок
 будемо мати іншу константу.
будемо мати іншу константу. . Тоді розв’язок буде мати вигляд
. Тоді розв’язок буде мати вигляд (4.19)
(4.19) (4.20)
(4.20) , використаємо початкову умову, з якої виходить
, використаємо початкову умову, з якої виходить
 виявляються коефіцієнтами розкладання функції
виявляються коефіцієнтами розкладання функції  у ряд Фур’є по синусам в інтервалі (0,1). Отже
у ряд Фур’є по синусам в інтервалі (0,1). Отже
 під інтеграл, тоді
під інтеграл, тоді
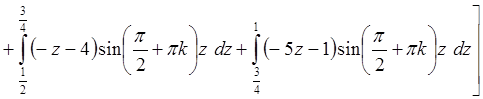 .
.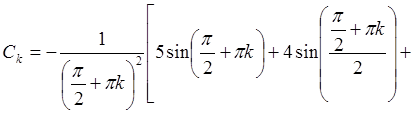
 (4.21)
(4.21) .
.


 (4.22)
(4.22) змінюється від 0 до 1 з кроком 0.2, а
змінюється від 0 до 1 з кроком 0.2, а  - від 0 до 1 з кроком 0.25. Змінення розподілу температури вздовж стержня з часом показано на графіках малюнку 4.2.
- від 0 до 1 з кроком 0.25. Змінення розподілу температури вздовж стержня з часом показано на графіках малюнку 4.2.

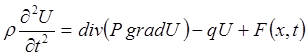 , (5.1)
, (5.1) - невідома функція, яка залежить від
- невідома функція, яка залежить від  , просторових координат
, просторових координат  і часу
і часу  ;
;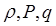 - коефіцієнти, які визначаються властивостями середовища, де відбувається коливальний процес;
- коефіцієнти, які визначаються властивостями середовища, де відбувається коливальний процес; - вільний доданок, висловлює інтенсивність зовнішнього збурення.
- вільний доданок, висловлює інтенсивність зовнішнього збурення.
 . (5.2)
. (5.2) струна виконує коливання біля свого положення рівноваги, яка співпадає з віссю
струна виконує коливання біля свого положення рівноваги, яка співпадає з віссю  . Величину відхилення струни від положення рівноваги в точці
. Величину відхилення струни від положення рівноваги в точці 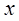 у час
у час  позначимо через
позначимо через  , так що
, так що  - є рівняння струни у час
- є рівняння струни у час  . Обмежуючись розглядом лише малих коливань струни, будемо нехтувати величинами порядку мализни в порівнянні з
. Обмежуючись розглядом лише малих коливань струни, будемо нехтувати величинами порядку мализни в порівнянні з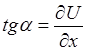 .
. в точці
в точці  у час
у час  направлений по дотичній до струни у точці
направлений по дотичній до струни у точці 















 0
0 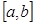 після відхилення від положення рівноваги у рамках даного приближення не змінює своєї довжини, тобто
після відхилення від положення рівноваги у рамках даного приближення не змінює своєї довжини, тобто
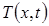 буде залишатися постійною, яка не залежить від
буде залишатися постійною, яка не залежить від  і
і  . Позначимо через
. Позначимо через 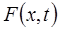 щільність зовнішніх сил, які діють на струну у точці
щільність зовнішніх сил, які діють на струну у точці  , а в час
, а в час  . Нехай
. Нехай 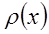 позначає лінійну щільність струни в точці
позначає лінійну щільність струни в точці  - маса елемента струни
- маса елемента струни 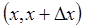 .
. діє сила натягу
діє сила натягу  , і зовнішня сила, сума яких, згідно законам Ньютона, повинна дорівнювати добутку маси цього елемента на його прискорення. Проектуючи цю векторну рівність на вісі, на основі вище сказаного, будемо мати
, і зовнішня сила, сума яких, згідно законам Ньютона, повинна дорівнювати добутку маси цього елемента на його прискорення. Проектуючи цю векторну рівність на вісі, на основі вище сказаного, будемо мати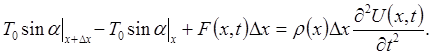 (5.3)
(5.3) ,
, ,
,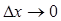 виходить рівність
виходить рівність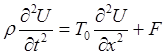 . (5.4)
. (5.4) коливання струни називаються вимушеними, а при
коливання струни називаються вимушеними, а при 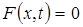 - вільними.
- вільними. стала,
стала,  , то рівняння коливань струни приймає вигляд
, то рівняння коливань струни приймає вигляд , (5.5)
, (5.5)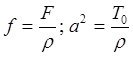 - сталі.
- сталі.
 , (2.1)
, (2.1) (2.2)
(2.2)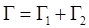 – повна межа розглядуваної області
– повна межа розглядуваної області  ).
). (2.3)
(2.3)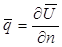 .
. та її межи
та її межи  (2.4)
(2.4) , (2.5)
, (2.5) – вагова функція;
– вагова функція; . (2.6)
. (2.6) . (2.7)
. (2.7) – повинна бути неперервною разом зі своїми другими похідними та задовольняти рівнянню
– повинна бути неперервною разом зі своїми другими похідними та задовольняти рівнянню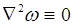 (2.8)
(2.8) . (2.9)
. (2.9) і
і  – шукані, а
– шукані, а  і
і  – задані.
– задані. розбити на скінчене число граничних елементів K1+K2, тобто
розбити на скінчене число граничних елементів K1+K2, тобто ,
, , то рівняння (2.9) матиме вигляд
, то рівняння (2.9) матиме вигляд . (2.10)
. (2.10)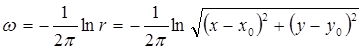 . (2.11)
. (2.11)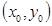 обираємо не на контурі, а на відстані
обираємо не на контурі, а на відстані  на зовнішній нормалі, де d – довжина елемента.
на зовнішній нормалі, де d – довжина елемента. (2.12)
(2.12)
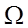 використовується співвідношення [1]
використовується співвідношення [1] , (2.13)
, (2.13) .
. – задані, q, U – знайдені величини, а
– задані, q, U – знайдені величини, а  – фундаментальний розв’язок (2.11), в якому за джерело
– фундаментальний розв’язок (2.11), в якому за джерело  береться внутрішня точка
береться внутрішня точка  .
. і
і  , де n – нормаль до кола, можна отримати формули для двох випадків.
, де n – нормаль до кола, можна отримати формули для двох випадків. (тут (a, b) – координати центру, R – радіус кола) перепишемо у вигляді
(тут (a, b) – координати центру, R – радіус кола) перепишемо у вигляді ;
;


 .
.


 y
y


 2 L2
2 L2



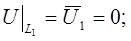 L3 L1
L3 L1 1 L4 L6
1 L4 L6

 0 1 L5 3 4 x
0 1 L5 3 4 x Мал. 2.1
Мал. 2.1
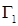 приймаємо суму L1+L2+L4+L5, а за контур
приймаємо суму L1+L2+L4+L5, а за контур  - суму L3+L6. Граничне рівняння має вигляд
- суму L3+L6. Граничне рівняння має вигляд
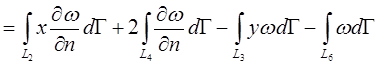 (*)
(*) ,
, ;
;