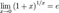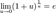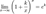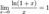Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения плоскости в пространстве.
Уравнения плоскости в пространстве. Ax+By+Сz-Ax0-By0-Сz0=0 - общ. Ур-е a (x – x 0) + b (y – y 0) + c (z – z 0) = 0
Угол между плоскостями, условие параллельности и перпендикулярности плоскостей. Угол между плоскостями:
Усл. перпендикулярности: Необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если: Усл. параллельности: Плоскости параллельны, векторы нормалей коллинеарны:
Расстояние от точки до плоскости.
Уравнения прямой в пространстве. Каноническое ур-е: Парам.ур-е: Ур-е прямой проход. Через 2 точки:
Угол между прямыми, условие параллельности и перпендикулярности прямых. Угол между двумя прямыми равен углу между их направляющими векторами а)
S1 {l1,m1} S2 {l2,m2},
Или p:y=k1x+b1, k1=tgj1 q:y=k2x+b2, k2=tgj2 =>tgj=tg(j2-j1)= =(tgj2-tgj1)/(1+ tgj1tgj2)= =(k2-k1)/(1+k1k2). б) p||q, tgj=0, k1=k2 в)p^q,то
Взаимное расположение прямой и плоскости, угол между прямой и плоскостью.
Угол между прямымой и плоскостью: cosα= Если α‖β, то s^n, => s . n=o Если α^β, то s‖n
Предел функции в точке. Число А – это предел функции y=f(x) в точке x0, если для любой последовательности допустимых значений для аргумента функции
Односторонние пределы. Число А называется левым односторонним пределом функции y=f(x), если х®x0 так что для лююбых х: Число А называется правым односторонним пределом функции y=f(x), если х®x0 так что для лююбых х:
9. Предел функции при Число А называется пределом функции y=f(x) при х®∞ если для любого сколь угодно малого положительного числа d найдется положительное число М что для любго Х так что
Бесконечно большие и бесконечно малые функции. Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если БЕСКОНЕЧНО БОЛЬШАЯ ФУНКЦИЯ - функция переменного х, к-рая в данном процессе изменения х становится и остается по абсолютной величине больше любого наперед заданного числа. Точнее, функция f(x), определенная в окрестности точки х0, наз. бесконечно большой функцией при х, стремящемся к x0, если для любого числа М > 0 найдется такое число δ = δ (М) > 0, что для всех х ≠ х0 и таких, что |х - х0 | < δ, выполняется неравенство |f(x)| > M. Этот факт записывается так:
Основные теоремы о б.м.ф. Т1: Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция. Т2: Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая. Т3: Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая. Т4: Если функция α(х) — бесконечно малая (α¹ 0), то функция 1/α(х) есть бесконечно большая функция и наоборот: если функция ƒ(х)— бесконечно большая, то 1/ƒ(х) — бесконечно малая.
Теорема о связи функции ее предела и б.м.ф. Для того чтобы число А было пределом функции f(x) в точке х0 необходимо и достаточн чтобы эта функция была представлена как сумма ее предела и б.м.ф.
Основные теоремы о пределах (предел суммы, произведения и частного функций) Теорема 1: предел суммы = сумме пределов - Теорема 2: предел произведения = произведению пределов - Теорема 3: предел частного двух функций = частному пределов -
Теорема о пределе промежуточной функции. Если функция f(x)заключена между двумя функцияи f(x) и g(x) стремящихся к одному и тому же пределу limf(x)=A, limg(x)=A, то и f(x) будет стремиться к тому же пределу.
Первый замечательный предел, его следствия.
1. 2. 3. 4. 5. Второй замечательный предел, его следствия.
Следствия:
Непрерывность функций в точке, на интервале.
x=x0+Dx, Dx=x-x0 Dy=f(x0+Dx)-f(x0) Ф-ция y=f(x) наз. непрерывной в точке x0, если она определена в окрестности этой точки, а limDy=0. (б.м. приращению аргумента соответствует б.м. приращению ф-ции). limDy=lim[f(x)-f(x0)]=limf(x)-limf(x0)=0, то limf(x)=limf(x0) x®x0 Ф-ция непрерывна в точке х0, если ее предел = значению этой ф-ции в точке х0 Ф-ция явл. непрерывной на интервале, если она непрерывна в каждой его точке.
Связь между непрерывностью и дифференцируемостью функции.
Теорема: Если функция дифференцируема в некоторой точке, то она непрерывна в ней.
Таблица производных.
Максимум и минимум функций. Точка x0 называется точкой минимума функции f, если для всех x из некоторой окрестности x0 выполняется неравенство f(x) ≥ f(x0. . Точка x0 называется точкой максимума функции f, если для всех x из некоторой окрестности x0 выполняется неравенство f(x) ≤ f(x0.
Асимптоты графика функции. Асимптота - прямая, к которой график ф-ции стремится, но никогда ее не пересекает. 1) прямая х=х0 назыв-ся вертикальной асимптотой графика ф-ции f(x)=y, если при х®х0 |f(x)|®+¥ (вида x=b) 2) y=kx+b,,y=f(x) - общее ур-е наклонной асимптоты lim[f(x)-(kx+b)]=0, f(x)=kx+b+a(б.м.в.) по св-ву x®¥ пределов. разделим левую и правую части на х. Возьмем предел при х®¥ f(x)/x=k+b/x+a/x, lim(f(x)/x)=limk+lim(b/x)+lim(a/x) x®¥ , то k=lim(f(x)/x) b=lim[f(x)-kx] Если эти пределы существуют, то существует и наклонная ассимптота вида kx+b=y 3)k=lim(f(x)/x)=0, y=b - горизонтальная асимптота.
Уравнения плоскости в пространстве. Ax+By+Сz-Ax0-By0-Сz0=0 - общ. Ур-е a (x – x 0) + b (y – y 0) + c (z – z 0) = 0
|
||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 86; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.147.252 (0.015 с.) |
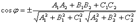
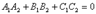 .
.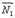 ïï
ïï 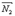 . Это условие выполняется, если:
. Это условие выполняется, если: 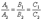
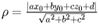 .
.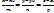
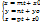
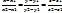

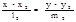
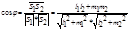

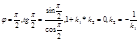
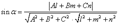 -угол
-угол
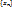 ®x0 соответствующие значения функции стремятся к числу А, т.е.
®x0 соответствующие значения функции стремятся к числу А, т.е. 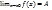
 <хо, т.е.
<хо, т.е. 
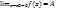

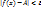
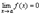 или
или 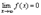 , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
, т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.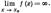
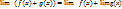
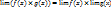




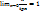
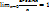
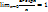
 или
или