
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поведенческие свойства сетей Петри.Стр 1 из 4Следующая ⇒
Лекция 4. Поведенческие свойства сетей Петри.
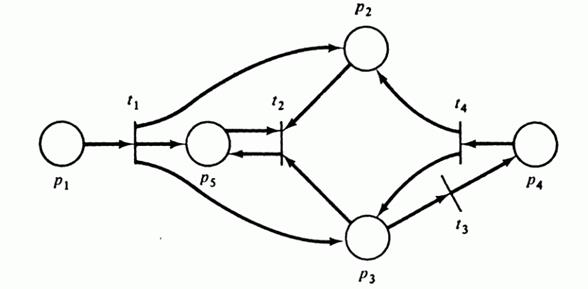
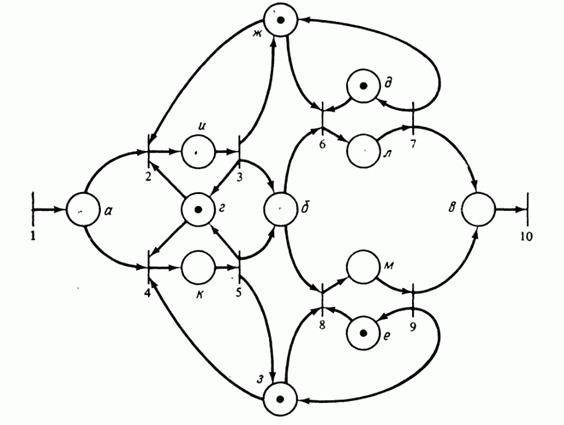
Пример сети Петри и её графа. C = (P, T, I, O), P = { p 1, p 2 p 3, p 4, p 5}, T = { t 1, t 2 t 3, t 4} I (t 1) = { p 1}, O (t 1) = { p 2, p 3, р 5}, I (t 2) = { p 2, p 3, p 5}, O (t 2) = { p 5}, I (t 3) = { p 3}, O (t 3) = { р 4}, I (t 4) = { p 4}, O (t 4) = { p 2, p 3}.
Рис 4.1: Примерсети Петри.
Привести пример какой-нибудь маркировки.
Функция следующего состояния. Состояние, сети Петри определяется ее маркировкой. Запуск перехода изменяет состояние сети. Пространство состояний сети Петри, обладающей n позициями, есть множество всех маркировок, т. е. Nn. Изменение в состоянии, вызванное запуском перехода, определяется функцией изменения d, которую мы назовем функцией следующего состояния:
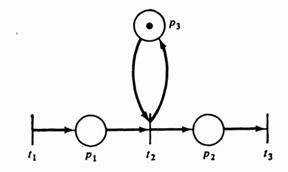
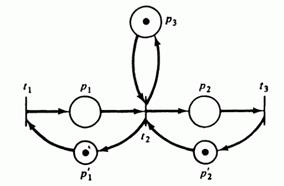
Достижимость. Пусть некоторый переход в маркировке m разрешен и, следовательно, может быть запущен. Результат запуска перехода есть новая маркировка m '. Говорят, что m ' является непосредственно достижимой из маркировки m. если существует переход Безопасность. Одно из важнейших свойств сети Петри, которая должна моделировать реальное устройство, — безопасность. Позиция сети Петри является безопасной, если число фишек в ней никогда не превышает 1. Позиция Если позиция не является кратной входной или кратной выходной для перехода, ее можно сделать безопасной. К позиции Если Если
Цель введения этой новой позиции
а) б)
Рис 4.2: а) Опасная сеть Петри; б) Эквивалентная ей безопасная сеть Петри.
Безопасность — это частный случай более общего свойства ограниченности. Позиция является k -безопасной или k -ограниченной, если количество фишек в ней не может превышать целое число k. Заметим, что граница по числу фишек, которые могут находиться в позиции, может быть функцией от позиции. Если позиция Сохранение. Сеть Петри C = (P, T, I, O) с начальной маркировкой m называется строго сохраняющей, если для всех
Строгое сохранение — это очень сильное ограничение. Например, из него следует, что число входов в каждый переход должно равняться числу выходов. Сеть Петри C = (P, T, I, O) с начальной маркировкой m называется сохраняющей по отношению к вектору взвешивания w, w = (w 1, w 2,.., wn), n = | P |, wi > 0, если для всех
Строго сохраняющая сеть Петри является сохраняющей по отношению к вектору взвешивания (1,..., 1). Активность. Тупик в сети Петри — это переход (или множество переходов), которые не могут быть запущены. В сети Переход называется активным, если он не заблокирован (нетупиковый). Это не означает, что переход разрешен, скорее он может быть разрешенным. Переход tj сети Петри С называется потенциально допустимым в маркировке m, если существует маркировка
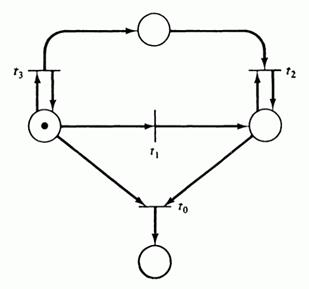
Для заданной маркировки m можно выделить пять уровней активности. Уровень 0: Переход tj обладает активностью уровня 0, если он никогда не может быть запущен. Уровень 1: Переход tj обладает активностью уровня 1, если он потенциально запустим, т. е. если существует такая Уровень 2: Переход tj; обладает активностью уровня 2, если для всякого целого n существует последовательность запусков, в которой tj присутствует по крайней мере n раз. Уровень 3: Переход tj обладает активностью уровня 3, если существует бесконечная последовательность запусков, в которой tj присутствует неограниченно часто. Уровень 4: Переход tj обладает активностью уровня 4, если для всякой Переход, обладающий активностью уровня 0, называется пассивным. Переход, обладающий активностью уровня 4, называется активным. Сеть Петри обладает активностью уровня i, если каждый ее переход обладает активностью уровня i. В качестве примера, иллюстрирующего уровни активности, рассмотрим сеть Петри на рис. 4.3. Переход t 0 не может быть запущен никогда; он пассивен. Переход t 1 можно запустить точно один раз; он обладает активностью уровня 1. Переход t 2 может быть запущен произвольное число раз, но это число зависит от числа запусков перехода t 3. Если мы хотим запустить t 2 пять раз, мы запускаем пять раз t 3 затем t 1 и после этого пять раз t 2. Однако, как только запустится t 1 (t 1 должен быть запущен до того, как будет запущен t 2), число возможных запусков t 2 станет фиксированным. Следовательно, t 2 обладает активностью уровня 2, но не уровня 3. С другой стороны, переход t 3 можно запускать бесконечное число раз, и поэтому он обладает активностью уровня 3, но не уровня 4, поскольку, как только запустится t 1, t 3 больше запустить будет нельзя.
Рис 4.3: Примерразличной степени активности переходов.
Методы анализа сетей Петри.
Дерево достижимости.
Рис 4.4: Маркированная сеть Петри, для которой строится дерево достижимости.
Дерево достижимости представляет множество достижимости сети Петри. Рассмотрим, например, маркированную сеть Петри на рис. 4.4. Её начальная маркировка – (1, 0, 0). Это – корневая вершина дерева достижимости. Непосредственно достижимые из неё маркировки – это вершины второго уровня и т.д.
Рис 4.5: Первые три шага построения дерева достижимости для сети Петри на рис 4.4. Получившееся дерево достижимости может оказаться бесконечным. Будет порождена каждая маркировка из множества достижимости, поэтому для любой сети Петри с бесконечным множеством достижимости соответствующее дерево также должно быть бесконечным. Даже сеть Петри с конечным множеством достижимости может иметь бесконечное дерево. Пассивные маркировки – маркировки, в которых нет разрешенных переходов. Они называются терминальными вершинами. Другой класс маркировок – это маркировки, ранее встречавшиеся в дереве. Они называются дублирующими вершинами; никакие последующие маркировки рассматривать нет нужды – все они будут порождены из места первого появления дублирующей маркировки в дереве. Таким образом, в дереве на рис.4.5 маркировка (0, 1, 1), получившаяся в результате выполнения последовательности
Для сведения дерева достижимости к конечному представлению используется еще одно средство. Рассмотрим последовательность запусков переходов σ, начинающуюся в начальной маркировке m и кончающуюся в маркировке m ' > m,. Маркировка m ' совпадает с маркировкой m, за исключением того, что имеет некоторые «дополнительные» фишки в некоторых позициях. Теперь, поскольку на запуски переходов лишние фишки не влияют, последовательность σ можно запустить снова, начиная в m ' и приходя к маркировке m ". В общем случае можно запустить последовательность σ n раз, получив в результате маркировку
Рис 4.6: Дерево достижимости для сети Петри изображённой на рис 4.4. Можно показать, что алгоритм построения дерева достижимости заканчивает работу.
Лекция 5. Сохранение. Если маркировка имеет
Если система (5.1) имеет решение, то сеть сохраняющая с весом. Покрываемость. Данная задача решается проверкой дерева достижимости. Строим для начальной маркировки дерево достижимости. Затем ищем любую вершину с m "
Матричные уравнения. Второй подход к анализу сетей Петри основан на матричном представлении сетей Петри. Представим сеть Петри в виде двух матриц
Пусть e [ j ] — m -вектор, содержащий нули везде, за исключением j -й компоненты. Переход tj представляется m -вектором e [ j ] (строка), а маркировка m — n -вектором (столбец). Теперь переход tj в маркировке m разрешен, если m
где D = Для последовательности запусков переходов
Вектор Сохранение. Для того чтобы показать сохранение, необходимо найти (ненулевой) вектор взвешивания, для которого взвешенная сумма по всем достижимым маркировкам постоянна. Пусть w — n - вектор-столбец. Тогда, если m — начальная маркировка, а m ' — произвольная достижимая маркировка, необходимо, чтобы m • w = m ' • w. Теперь, поскольку m ' достижима, существует последовательность запусков переходов
Следовательно, m • w = m ' • w = (m + Достижимость. Предположим, что маркировка m ' достижима из маркировки m. Тогда существует последовательность (возможно, пустая) запусков переходов
Пример. Рассмотрим маркированную сеть Петри на рис. 5.1. Матрицы
Рис 5.1: Примерсети Петри (решение задачи достижимости).
Для определения того, является ли маркировка (1, 8, 0, 1) достижимой из маркировки (1, 0, 1, 0), имеем уравнение
которое имеет решение х = (0, 4, 5). Это соответствует, например, последовательности
Матричный подход к анализу сетей Петри очень перспективен, но имеет и некоторые трудности. Заметим прежде всего, что матрица D сама по себе не полностью отражает структуру сети Петри. Переходы, имеющие как входы, так и выходы из одной позиции (петли), представляются соответствующими элементами матриц Другая проблема — это отсутствие информации о последовательности запусков. Еще одна трудность заключается в том, что наличие целочисленного решения уравнения (5.6) является необходимым для достижимости, но недостаточным. Рассмотрим простую сеть Петри, приведенную на рис. 5.2. Если мы хотим определить, является ли маркировка (0, 0, 0, 1) достижимой из маркировки (1, 0, 0, 0), необходимо решить уравнение
Это уравнение имеет решение (1, 1), соответствующее двум последовательностям:
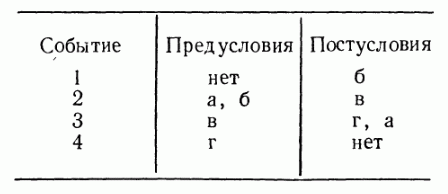
Рис 5.2: Сеть Петри, показывающая, что решение матричного уравнения — ЯЗЫКИ СЕТЕЙ ПЕТРИ. Лекция 6. События и условия. Простое представление системы сетью Петри основано на двух основополагающих понятиях: событиях и условиях. События — это действия, имеющие место в системе. Возникновением событий управляет состояние системы Состояние системы может быть описано множеством условий. Условие может принимать либо значение «истина», либо значение «ложь». Для того чтобы событие произошло, необходимо выполнение соответствующих условий. Эти условия называются предусловиями события. Возникновение события может вызвать нарушение предусловий и может привести к выполнению других условий, постусловий. В качестве примера рассмотрим задачу моделирования простого автомата-продавца. Автомат-продавец находится в состоянии ожидания до тех пор, пока не появится заказ, который он выполняет и посылает на доставку. Условиями для такой системы являются: а) автомат-продавец ждет; б) заказ прибыл и ждет; в) автомат-продавец выполняет заказ; г) заказ выполнен. Событиями будут: 1. Заказ поступил. 2. Автомат-продавец начинает выполнение заказа. 3 Автомат-продавец заканчивает выполнение заказа. 4. Заказ посылается на доставку. Таблица предусловий и постусловий:
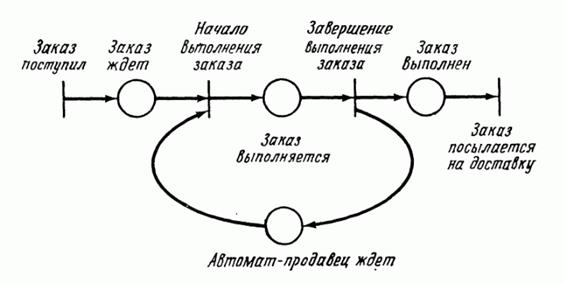
В сети Петри условия моделируются позициями, события — переходами. При этом входы перехода являются предусловиями соответствующего события; выходы — постусловиями. Возникновение события равносильно запуску соответствующего перехода. Выполнение условия представляется фишкой в позиции, соответствующей этому условию. Запуск перехода удаляет разрешающие фишки, представляющие выполнение предусловий и образует новые фишки, которые представляют выполнение постусловий. Сеть Петри на рис.6.1 иллюстрирует модель приведенного выше автомата-продавца.
Рис 6.1: Сеть Петри для простого автомата-продавца.
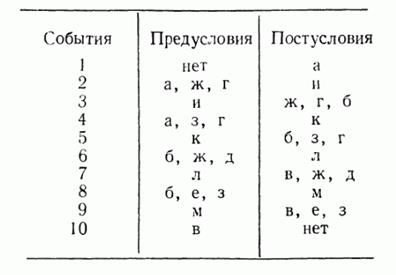
Более сложная система. Система автоавтомат-продавец состоит из трех различных автоматов M1, М2 и М3 и двух операторов F1 и F2. Оператор F1 воздействует на автоматы М1 и М2, а оператор F2 — на М1 и М3. Заказы требуют двух стадий обработки. Сначала они должны быть обработаны автоматом М1, затем либо автоматом М2 либо М3. Эта система будет иметь следующие условия: а) заказ прибыл и ждет обработки автоматом М1. б) заказ обработан автоматом М1 и ждет обработки либо автоматом М2, либо М3; в) заказ выполнен; г) автомат M1 незанят; д) автомат М2 незанят; е) автомат М3 незанят; ж) оператор F1 незанят; з) оператор F2 незанят; и) автомат М1 находится под воздействием оператора F1; к) автомат М1 находится под воздействием оператора F2, л) автомат М2 находится под воздействием оператора F1, м) автомат М3 находится под воздействием оператора F2. При этом могут происходить следующие события: 1. Поступление заказа. 2. Оператор F1 начинает выполнение заказа на автомате M1 3. Оператор F1 закончил выполнение заказа на автомате М1. 4. Оператор F2 начинает выполнение заказа на автомате М1. 5. Оператор F2 закончил выполнение заказа на автомате М1. 6. Оператор F1 начинает выполнение заказа на М2. 7. Оператор F1 закончил выполнение заказа на М2. 8. Оператор F2 начинает выполнение заказа на М3. 9. Оператор F2 закончил выполнение заказа на М3. 10. Заказ посылается на доставку. Таблица предусловий и постусловий:
Рис 6.2: Сеть Петри для сложного автомата-продавца.
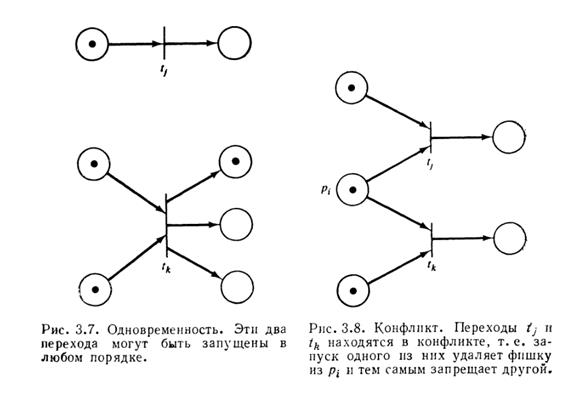
Одновременность и конфликт. В сети Петри два разрешенных невзаимодействующих события могут происходить независимо друг от друга. Сети Петри представляются идеальными для моделирования систем с распределенным управлением, в которых несколько процессов выполняются одновременно. В сети Петри отсутствует измерение времени или течение времени. Выполнение сети Петри (или поведение моделируемой системы) рассматривается как последовательность дискретных событий. Порядок появления событий является одним из возможных, допускаемых основной структурой. Это приводит к явной недетерминированности в выполнении сети Петри. Если в какой-то момент времени разрешено более одного перехода, то любой из нескольких возможных переходов может стать «следующим» запускаемым. Выбор запускаемого перехода осуществляется недетерминированным образом, т. е. случайно. Эта особенность сети Петри отражает тот факт, что в реальной жизненной ситуации, где несколько действий происходит одновременно, возникающий порядок появления событий — не однозначен; может возникнуть любая из множества последовательностей событий. Однако частичный порядок появления события — единственен. Для простоты обычно вводят следующее ограничение. Запуск перехода (и соответствующего события) рассматривается как мгновенное событие, занимающее нулевое время, и возникновение двух событий одновременно невозможно. Моделируемое таким образом событие называется примитивным; примитивные события мгновенны и неодновременны.
Рис 6.3: Понятие одновременности и конфликта в Сетях Петри.
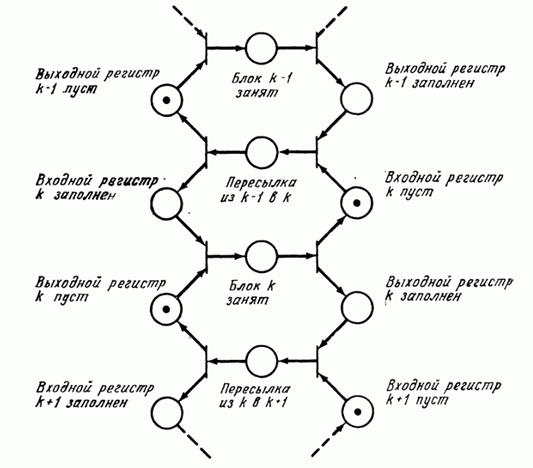
Аппаратное обеспечение ЭВМ. ЭВМ с конвейерной обработкой. Конвейер состоит из набора операций, которые могут выполняться одновременно. Когда операция k завершается, она передает свой результат операции (k + 1) и ожидает от операции (k — 1) нового задания. Для управления блоком k асинхронного конвейера необходимо знать, когда выполняются следующие условия: • входной регистр заполнен; • входной регистр пуст; • выходной регистр заполнен; • выходной регистр пуст; • блок занят; • блок свободен; • пересылка осуществлена.
Рис 6.4: Модель сети Петри устройства управления асинхронной ЭВМ с конвейерной обработкой.
Кратные функциональные блоки. Каждому функциональному блоку и каждому регистру поставим в соответствие позицию: если блок или регистр свободен — в позицию будет помещена фишка, если нет — фишки в позиции не будет. Кратные идентичные функциональные блоки показываются соответствующим числом фишек в позициях. На рис. 6.5 изображена часть сети Петри, которая может быть использована для моделирования выполнения инструкции, использующей блок u и регистры i, j и k.
Рис 6.5: Часть сети Петри, моделирующая устройство управления для ЭВМ с кратными регистрами и кратными функциональными блоками.
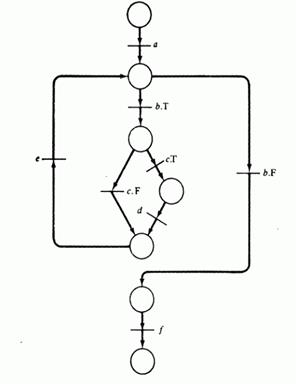
Рис 6.6: Перевод узлов вычисления и принятия решения в блок-схеме в переходы в сети Петри.
Рис 6.7: Пример блок-схемы и соответствующей ей сети Петри
Фишка, находящаяся в позиции, означает, что счетчик команд установлен на готовность выполнения следующей инструкции. Каждая позиция имеет единственный выходной переход, за исключением позиции, которая предшествует принятию решения; такие позиции имеют по два выходных перехода, соответствующих истинному и ложному значению предиката. Переходы связываются с действиями программы: вычислениями и принятиями решений. Переходы для вычислений имеют один вход и один выход; переход, представляющий вычисления, не может находиться в конфликте, поскольку его входная позиция не является входной для какого-либо другого перехода. Действие же, связанное с принятием решения, вводит в сеть конфликт. Выбор способа разрешения конфликта либо недетерминирован, либо им можно управлять извне (предсказателем, вычисляющим истинность или ложность предиката и вынуждающим запуск нужного перехода). Различие между этими двумя способами разрешения конфликта — методологический вопрос.
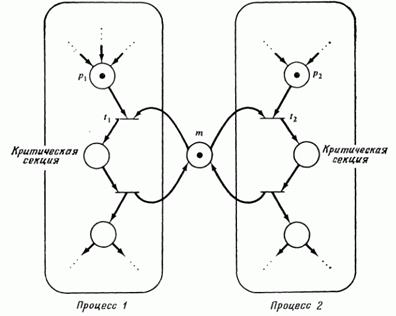
Синхронизация. Введение параллелизма полезно только в том случае, когда компоненты процессов могут взаимодействовать при получении решения задачи. Такое взаимодействие требует распределения ресурсов между процессами. Для гарантии правильности работы системы в целом распределением необходимо управлять. Проблемы синхронизации, возникающие при взаимодействии процессов, иллюстрируются многочисленными примерами, приведенными в литературе. Среди задач синхронизации: задача о взаимном исключении, задача о производителе/потребителе, задача об обедающих мудрецах, задача о чтении/записи и др. Задача о взаимном исключении. Взаимное исключение — это метод создания таких программ, что одновременно не более чем один процесс имеет доступ к разделяемому объекту данных. Участок кода, в котором осуществляется доступ к разделяемому объекту и который требует защиты от вмешательства других процессов, называется критической секцией.
Рис 6.8: Взаимное исключение. Управление доступом к критическим секциям осуществляется таким образом, что оба процесса не могут одновременно выполнять свои критические секции.
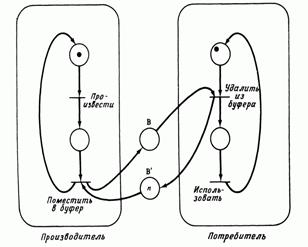
Задача о производителе/потребителе.
Рис 6.9: Задача о производителе/потребителе, моделируемая сетью Петри. Справа: задача о производителе/потребителе с ограниченным буфером. Буфер, представленный позициями В и В', ограничен п ячейками.
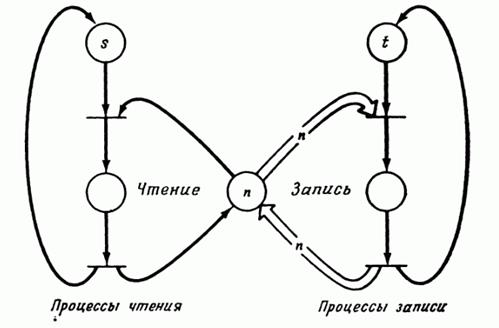
В задаче о производителе/потребителе также присутствует совместно используемый объект, но в этом случае разделяемый объект точно определен и является буфером. Процесс-производитель создает объекты, которые помещаются в буфер. Потребитель ждет, пока объект не будет помещен в буфер, удаляет его оттуда и использует. Один из вариантов — задача о нескольких производителях/нескольких потребителях. Его модель сетью Петри совпадает с сетью на рис. 6.9 (слева), за исключением того, что для представления s производителей и t потребителей мы начали выполнение сети с s фишками в начальной позиции процесса-производителя и t фишками в начальной позиции процесса-потребителя. В другом варианте задачи используется буфер ограниченного размера. Следовательно, производитель не может постоянно работать с той скоростью, которая ему нужна, а вынужден ждать, если потребитель работает медленно и буфер заполнен. На рис. 6.9 (справа) показано решение этой проблемы. Ограниченному буферу сопоставляются две позиции: В представляет количество элементов данных, которые произведены, но еще не использованы (число заполненных ячеек), В' — количество пустых ячеек в буфере. Первоначально В' имеет n фишек, а В фишек не имеет. Задача о чтении/записи. Существует несколько вариантов задачи о чтении/записи, однако основная структура их остается неизменной. Имеются процессы двух типов: процессы чтения и процессы записи. Все процессы совместно используют общий файл или переменную или элемент данных. Процессы чтения не изменяют объект в отличие от процессов записи. Таким образом, процесс записи должен взаимно исключать все другие процессы чтения и записи, в то время как несколько процессов чтения могут иметь доступ к разделяемым данным одновременно. Задача состоит в определении структуры управления, которая не приведет к тупику и не допустит нарушения критерия взаимного исключения. На рис. 6.10 иллюстрируется решение задачи в том случае, когда количество процессов чтения ограничено величиной n.
Рис 6.10: Задача о чтении/записи в случае, когда число процессов чтения ограничено величиной n. Первоначально имеются s процессов чтения и t процессов записи.
Проблема возникает в том случае, если количество процессов чтения не ограничено. Это связано с тем, что в сетях Петри нет механизма, который бы осуществлял проверку на нуль неограниченной позиции.
Лекция 7. Рис.1: Классификация систем массового обслуживания. . К замкнутым относятся системы, в которых поступающий поток требований ограничен. Например, мастер, задачей которого является наладка станков в цехе, должен периодически их обслуживать. Каждый налаженный станок становится в будущем потенциальным источником требований на подналадку. В подобных системах общее число циркулирующих требований конечно и чаще всего постоянно. Если питающий источник обладает бесконечным числом требований, то системы называются разомкнутыми. Примерами подобных систем могут служить магазины, кассы вокзалов, портов и др. Для этих систем поступающий поток требований можно считать неограниченным. Под дисциплиной подключения каналов к обслуживанию понимают правила, по которым обслуживающие приборы подключаются к обслуживанию поступающих заявок, при этом все заявки считаются равноценными, с этой точки зрения различают две разновидности СМО: системы со взаимопомощью между каналами обслуживания и системы без взаимопомощи. Встречаются СМО, в которых для ускорения процесса обслуживания допускается подключение нескольких каналов к работе над одной заявкой. Например, два или несколько рабочих могут одновременно ремонтировать один станок или автомашину, по одному самолету может стрелять несколько зенитных орудий, вычисления для одной задачи могут быть, распараллелены между несколькими ЭВМ Многофазными называются СМО, которые состоят из нескольких последовательно соединенных отдельных подсистем массового обслуживания, причем входящий поток каждой последующей подсистемы является выходящим потоком предыдущей. Характеристики СМО. 1. Среднее число требований, поступающих в систему обслуживания за единицу времени, называется интенсивностью поступления требований иопределяется следующим соотношением: 2. Интенсивность обслуживания среднее число требований, обслуженных системой за единицу времени 3. Коэффициент загрузки:
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 2739; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.190.147 (0.21 с.) |
 ,
,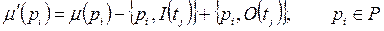 . (4.1)
. (4.1)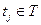 , такой, что
, такой, что 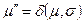 , где σ — последовательность переходов. Определим множество достижимости R (C, m) сети Петри С с маркировкой m как множество всех маркировок, достижимых из m. Маркировка m ' принадлежит R (C, m), если существует какая-либо последовательность запусков переходов, изменяющих m на m '.
, где σ — последовательность переходов. Определим множество достижимости R (C, m) сети Петри С с маркировкой m как множество всех маркировок, достижимых из m. Маркировка m ' принадлежит R (C, m), если существует какая-либо последовательность запусков переходов, изменяющих m на m '.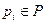 сети Петри C = (P, T, I, O) с начальной маркировкой m является безопасной, если
сети Петри C = (P, T, I, O) с начальной маркировкой m является безопасной, если 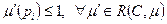 . Сеть Петри безопасна, если безопасны все позиции сети. В первоначальном определении сети Петри были безопасны, поскольку переход не мог быть запущен, если не все из выходных позиций были пусты (а кратные дуги не были разрешены).
. Сеть Петри безопасна, если безопасны все позиции сети. В первоначальном определении сети Петри были безопасны, поскольку переход не мог быть запущен, если не все из выходных позиций были пусты (а кратные дуги не были разрешены).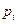 , которую необходимо сделать безопасной, добавляется новая позиция
, которую необходимо сделать безопасной, добавляется новая позиция 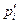 Переходы, в которых
Переходы, в которых  и
и 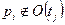 , тогда добавить
, тогда добавить 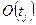
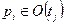 и
и 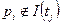 , тогда добавить
, тогда добавить 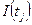 .
.
 имеет место
имеет место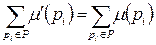 . (4.2)
. (4.2)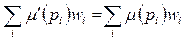 . (4.3)
. (4.3)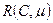 . Следовательно, если переход активен, то всегда возможно перевести сеть Петри из ее текущей маркировки в маркировку, в которой запуск перехода станет разрешенным.
. Следовательно, если переход активен, то всегда возможно перевести сеть Петри из ее текущей маркировки в маркировку, в которой запуск перехода станет разрешенным.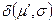 .
.




 , не будет порождать какие-либо новые вершины, поскольку она ранее встречалась в дереве в результате выполнения перехода
, не будет порождать какие-либо новые вершины, поскольку она ранее встречалась в дереве в результате выполнения перехода  из начальной маркировки.
из начальной маркировки. . Следовательно, для тех позиций, которые увеличивают число фишек последовательностью σ, можно создать произвольно большое число фишек, просто повторяя последовательность σ столько, сколько это нужно. В сети Петри на рис. 4.4, например, можно запустить переход
. Следовательно, для тех позиций, которые увеличивают число фишек последовательностью σ, можно создать произвольно большое число фишек, просто повторяя последовательность σ столько, сколько это нужно. В сети Петри на рис. 4.4, например, можно запустить переход  столько раз, сколько необходимо для того, чтобы получить произвольное число фишек в р 2. Представим бесконечное число маркировок, получающихся из циклов такого типа, с помощью специального символа ω, который обозначает «бесконечность». Для любого постоянного а определим
столько раз, сколько необходимо для того, чтобы получить произвольное число фишек в р 2. Представим бесконечное число маркировок, получающихся из циклов такого типа, с помощью специального символа ω, который обозначает «бесконечность». Для любого постоянного а определим . (4.5)
. (4.5)
 в качестве маркировки некоторой позиции тогда для того, чтобы сеть была сохраняющей, вес этой позиции должен быть равным 0. Если сеть сохраняющая, существуют взвешенная сумма, обозначим её s, и вектор весов w = (w 1, w 2,.., wn). Для каждой маркировки дерева достижимости имеем
в качестве маркировки некоторой позиции тогда для того, чтобы сеть была сохраняющей, вес этой позиции должен быть равным 0. Если сеть сохраняющая, существуют взвешенная сумма, обозначим её s, и вектор весов w = (w 1, w 2,.., wn). Для каждой маркировки дерева достижимости имеем . (5.1)
. (5.1) m '. Если такой вершины не существует, маркировка m ' не покрывается никакой достижимой маркировкой; если она найдена, то это и есть искомая маркировка. Путь от корня к покрывающей маркировке определяет последовательность переходов, которые приводят из начальной маркировки к покрывающей маркировке. Символ
m '. Если такой вершины не существует, маркировка m ' не покрывается никакой достижимой маркировкой; если она найдена, то это и есть искомая маркировка. Путь от корня к покрывающей маркировке определяет последовательность переходов, которые приводят из начальной маркировки к покрывающей маркировке. Символ 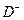 и
и 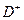 , представляющих входную и выходную функции. Каждая матрица имеет m строк (по одной на переход) и n столбцов (по одному на позицию). Определим
, представляющих входную и выходную функции. Каждая матрица имеет m строк (по одной на переход) и n столбцов (по одному на позицию). Определим (5.2)
(5.2)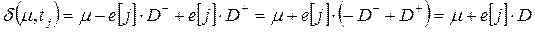 . (5.3)
. (5.3)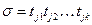 имеем
имеем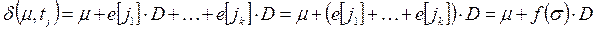 . (5.4)
. (5.4)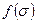 называется вектором запусков последовательности
называется вектором запусков последовательности 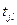 в последовательности
в последовательности 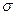 , которая переводит сеть из m в m '. Поэтому
, которая переводит сеть из m в m '. Поэтому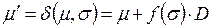 . (5.5)
. (5.5)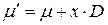 . (5.6)
. (5.6)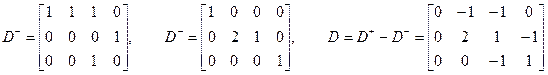 . (5.7)
. (5.7)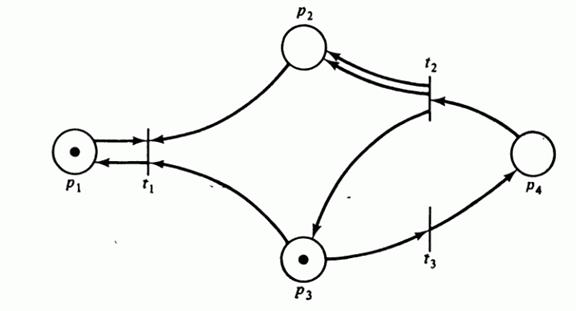
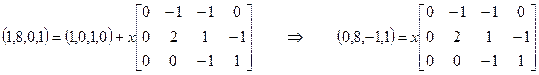 . (5.8)
. (5.8)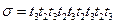 . (В принципе, может быть и другая последовательность.)
. (В принципе, может быть и другая последовательность.)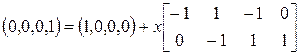 . (5.9)
. (5.9)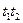 и
и 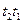 . Но ни одна из этих двух последовательностей переходов невозможна, поскольку в (1,0, 0, 0) ни
. Но ни одна из этих двух последовательностей переходов невозможна, поскольку в (1,0, 0, 0) ни 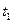 ни
ни 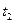 не разрешены.
не разрешены.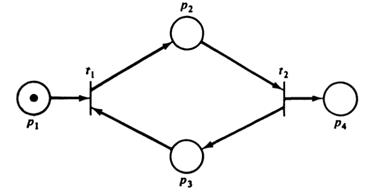



 , где Т — среднее значение интервала между поступлением очередных требований.
, где Т — среднее значение интервала между поступлением очередных требований. , tобс — среднее время обслуживания.
, tобс — среднее время обслуживания.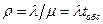 .
.


