
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Физический и математический маятники
Физическим маятником называется абсолютно твердое тело, совершающее колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, не проходящей через его центр масс. На рисунке 33.1 изображено произвольное тело массой
Рис. 33.1
Пусть ось вращения (качания) маятника является осью Если силами трения в подвесе маятника можно пренебречь, то момент относительно оси
направленный в противоположную оси
С другой стороны, согласно основному уравнению динамики вращения твердого тела
Так как
где При малых колебаниях маятника
решение которого имеет вид
где
Математический маятником называется материальная точка (частица), подвешенная на невесомой и нерастяжимой нити (длиной Математический маятник представляет собой предельный случай физического маятника, вся масса Период колебаний математического маятника зависит только от его длины и ускорения свободного падения:
Возвращающей силой в этом случае является проекция силы тяжести на направление движения (
Пример 33.1. Диск радиусом Решение. Период колебаний физического маятника определяется по формуле (33.4),
где Момент инерции
где Учитывая, что для диска
и по условию задачи
представим (33.5) в виде
Подставляя выражение (33.6) в формулу (33.4), получаем окончательно
Ответ:
Вопросы: 1) Какие колебания называют гармоническими? собственными? 2) Что такое смещение? 3) Дайте определение амплитуды, фазы, периода, частоты, циклической частоты. 4) Какая сила называется квазиупругой? Приведите примеры квазиупругих сил. 5) От чего зависят амплитуда и начальная фаза гармонических колебаний? 6) Как зависит ускорение гармонических колебаний от смещения? 7) Выведите формулу для полной энергии при гармонических колебаниях. 8) Какую систему можно считать математическим маятником?
Лекция 10. Механические колебания (продолжение)
Затухающие колебания
Во всех реальных случаях помимо квазиупругой силы на тело действует сила сопротивления, которая обычно считается пропорциональной скорости:
где Уравнение второго закона Ньютона при наличии силы сопротивления имеет вид
или
где
где Из выражения (34.2) видно, что амплитуда колебаний не является постоянной величиной, а уменьшается со временем по экспоненциальному закону:
где
Рис. 34.1.
Следовательно, колебания при наличии силы сопротивления не являются гармоническими. Такие колебания называются затухающими. Постоянная величина
Поэтому период Быстроту убывания амплитуды характеризуют величиной, называемой логарифмическим декрементом затухания
где Воспользовавшись соотношением (34.3), получим
откуда
Пример 34.1. А мплитуда затухающих колебаний уменьшилась в Решение. Логарифмический декремент затухания связан с коэффициентом затухания Амплитуда затухающих колебаний убывает со временем по закону
По условию задачи
Комбинируя выражения (34.6) и (34.7), получаем
где Период колебаний
Подставляя выражения (34.9) и (34.8) в соотношение (34.5), получаем
Вынужденные колебания
Для поддержания колебаний в системе необходимо, чтобы действовала сила, работа которой компенсировала бы уменьшение механической энергии. Эта сила должна быть переменной, т.к. постоянная сила может только изменить положение равновесия, но не может способствовать поддержанию колебаний в системе. Колебания, возникающие в системе под действием внешней переменной силы, называются вынужденными. Переменная сила, поддерживающая в системе незатухающие колебания, называется вынуждающей. Рассмотрим простейший частный случай вынужденных колебаний в среде, заключающийся в том, что на систему действует сила, которая изменяется со временем по гармоническому закону:
где Помимо вынуждающей силы на тело действуют квазиупругая сила и сила сопротивления. Тогда колебания будут описываться дифференциальным уравнением:
или
где С течением времени собственные колебания в системе затухнут, следовательно, вынужденные колебания происходят с частотой вынуждающей силы. Решение уравнения для установившихся вынужденных колебаний имеет вид:
где
Из соотношений (35.4) и (35.5) следует, что амплитуда и фаза зависят от соотношения между частотой собственных колебаний Явление резкого увеличения амплитуды вынужденных колебаний при совпадении частоты вынуждающей силы с частотой собственных колебаний системы, называется резонансом.
Рис.35.1
Резонансная амплитуда зависит от сопротивления среды, как видно из формулы (35.4). Кривой
Тогда скорость изменяется по закону
откуда видно, что скорость изменяется в фазе с вынуждающей силой. Возрастание амплитуды при резонансе объясняется тем, что при
|
|||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 975; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.228 (0.061 с.) |
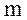 , колеблющееся вокруг оси
, колеблющееся вокруг оси 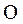 (ось
(ось 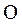 перпендикулярна плоскости чертежа);
перпендикулярна плоскости чертежа); 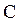 – центр масс;
– центр масс; 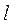 – плечо силы тяжести.
– плечо силы тяжести. 
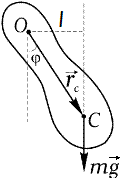
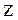 декартовой системы координат с началом в точке
декартовой системы координат с началом в точке 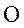 . Свяжем положительное направление оси
. Свяжем положительное направление оси 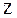 с положительным направлением отсчета угла поворота
с положительным направлением отсчета угла поворота 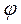 правилом правого винта. (Примем направление отсчета угла
правилом правого винта. (Примем направление отсчета угла 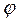 против часовой стрелки за положительное.) Тогда ось
против часовой стрелки за положительное.) Тогда ось 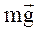 . Под действием этой силы при отклонении маятника на угол
. Под действием этой силы при отклонении маятника на угол 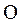
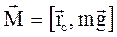 ,
,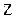 сторону. Тогда проекция вектора
сторону. Тогда проекция вектора 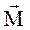 на ось
на ось 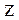
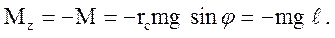 (33.1)
(33.1)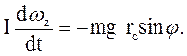 (33.2)
(33.2)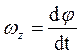 , то (33.2) можно переписать в виде
, то (33.2) можно переписать в виде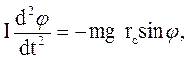
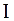 – момент инерции маятника относительно оси качания
– момент инерции маятника относительно оси качания 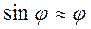 , и уравнение (33.2) принимает вид дифференциального уравнения гармонических колебаний,
, и уравнение (33.2) принимает вид дифференциального уравнения гармонических колебаний,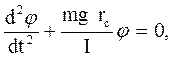
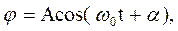 (33.3)
(33.3)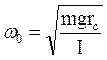 – собственная частота колебаний физического маятника, зависящая, как видно из приведенной формулы, от массы, момента инерции тела и расстояния между осью вращения и центром масс. В соответствии с формулами (28.2) и (33.3) период колебаний физического маятника определяется выражением
– собственная частота колебаний физического маятника, зависящая, как видно из приведенной формулы, от массы, момента инерции тела и расстояния между осью вращения и центром масс. В соответствии с формулами (28.2) и (33.3) период колебаний физического маятника определяется выражением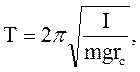 (33.4)
(33.4)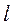 ) и совершающая колебания в вертикальной плоскости под действием силы тяжести.
) и совершающая колебания в вертикальной плоскости под действием силы тяжести.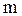 которого сосредоточена в его центре масс, так что
которого сосредоточена в его центре масс, так что 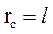 ,
, 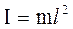 .
.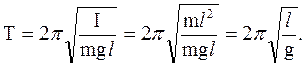
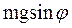 ). Для постоянства коэффициента
). Для постоянства коэффициента 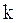 , а следовательно, и частоты колебаний
, а следовательно, и частоты колебаний 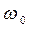 , необходимо постоянство длины нити
, необходимо постоянство длины нити 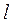 . Между тем составляющая силы тяжести
. Между тем составляющая силы тяжести 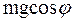 , действующая вдоль нити, может вызывать ее удлинение, которое будет минимальным в крайних положениях и максимальным при прохождении тела через положение равновесия. Поэтому для того чтобы колебания маятника были гармоническими, необходимо, кроме малости углов отклонения, дополнительно еще и условие нерастяжимости нити.
, действующая вдоль нити, может вызывать ее удлинение, которое будет минимальным в крайних положениях и максимальным при прохождении тела через положение равновесия. Поэтому для того чтобы колебания маятника были гармоническими, необходимо, кроме малости углов отклонения, дополнительно еще и условие нерастяжимости нити.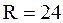 см колеблется около горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Определить период колебаний такого маятника.
см колеблется около горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Определить период колебаний такого маятника.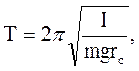
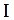 – момент инерции маятника относительно оси колебаний,
– момент инерции маятника относительно оси колебаний, 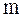 – его масса,
– его масса, 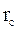 – расстояние от центра масс маятника до его оси колебаний.
– расстояние от центра масс маятника до его оси колебаний.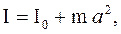 (33.5)
(33.5)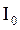 – момент инерции диска относительно оси, проходящей через центр масс параллельно оси колебаний,
– момент инерции диска относительно оси, проходящей через центр масс параллельно оси колебаний, 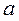 – расстояние между указанными осями.
– расстояние между указанными осями.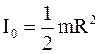

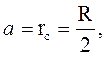
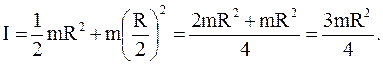 (33.6)
(33.6)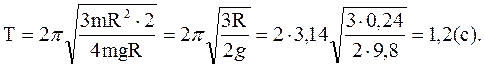
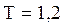 с.
с.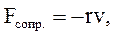
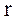 – коэффициент сопротивления.
– коэффициент сопротивления.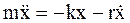
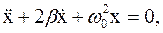 (34.1)
(34.1)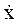 означает первую производную смещения по времени;
означает первую производную смещения по времени; 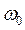 – частота собственных колебаний,
– частота собственных колебаний, 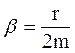 – коэффициент затухания. Уравнение (34.1) является дифференциальным. Его решение при не слишком сильном затухании имеет вид
– коэффициент затухания. Уравнение (34.1) является дифференциальным. Его решение при не слишком сильном затухании имеет вид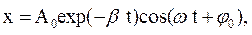 (34.2)
(34.2)
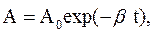 (34.3)
(34.3)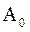 – начальная амплитуда колебаний.
– начальная амплитуда колебаний.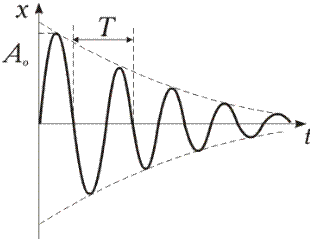
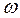 называется круговой частотой затухающих колебаний. Величина
называется круговой частотой затухающих колебаний. Величина 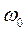 является круговой частотой колебаний в отсутствие сопротивления среды (
является круговой частотой колебаний в отсутствие сопротивления среды (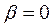 ) и называется собственной частотой колебаний. За счет работы силы сопротивления механическая энергия в процессе колебаний непрерывно уменьшается, переходя во внутреннюю энергию. Соответственно амплитуда колебаний уменьшается, и колебания постепенно затухают (рис. 34.1). Однако смещение
) и называется собственной частотой колебаний. За счет работы силы сопротивления механическая энергия в процессе колебаний непрерывно уменьшается, переходя во внутреннюю энергию. Соответственно амплитуда колебаний уменьшается, и колебания постепенно затухают (рис. 34.1). Однако смещение 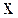 принимает нулевые значения через равные промежутки времени
принимает нулевые значения через равные промежутки времени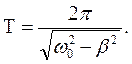 (34.4)
(34.4)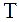 , определяемый формулой (34.4), и частота
, определяемый формулой (34.4), и частота 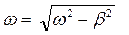 рассматриваются как условные период и частота затухающих колебаний.
рассматриваются как условные период и частота затухающих колебаний.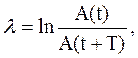
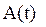 и
и 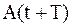 – значения амплитуд, соответствующих моментам времени, отличающимся на период.
– значения амплитуд, соответствующих моментам времени, отличающимся на период.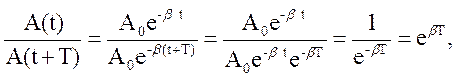
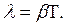 (34.5)
(34.5)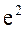 раз за
раз за 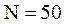 колебаний. Чему равен логарифмический декремент затухания
колебаний. Чему равен логарифмический декремент затухания  ?
?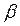 соотношением (34.5).
соотношением (34.5).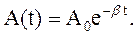 (34.6)
(34.6)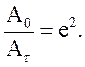 (34.7)
(34.7)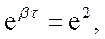
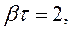
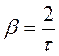 (34.8)
(34.8)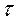 – время, в течение которого произошло
– время, в течение которого произошло 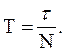 (34.9)
(34.9)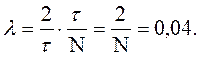
 Ответ:
Ответ: 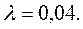
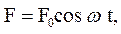 (35.1)
(35.1) – амплитуда силы,
– амплитуда силы, 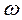 – круговая частота изменения силы со временем.
– круговая частота изменения силы со временем.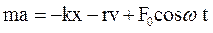
 (35.2)
(35.2)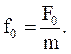
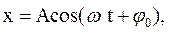 (35.3)
(35.3)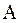 – амплитуда вынужденных колебаний,
– амплитуда вынужденных колебаний, 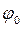 – сдвиг фаз; он представляет собой величину отставания по фазе вынужденного колебания от обусловившей его вынуждающей силы:
– сдвиг фаз; он представляет собой величину отставания по фазе вынужденного колебания от обусловившей его вынуждающей силы: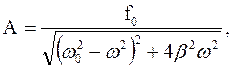 (35.4)
(35.4)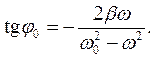 (35.5)
(35.5)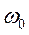 и частотой вынуждающей силы
и частотой вынуждающей силы 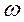 . При совпадении этих частот амплитуда колебаний будет резко возрастать (рис.35.1)
. При совпадении этих частот амплитуда колебаний будет резко возрастать (рис.35.1)
 соответствует меньшее сопротивление среды, чем кривой
соответствует меньшее сопротивление среды, чем кривой 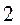 . При
. При 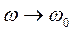 , как видно из (35.5),
, как видно из (35.5), 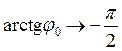 и, соответственно, решение уравнения колебаний приобретает вид
и, соответственно, решение уравнения колебаний приобретает вид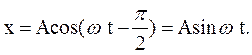
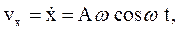
 направление вынуждающей силы все время совпадает с направлением перемещения, и, следовательно, вынуждающая сила будет непрерывно совершать положительную работу. Т.о., механическая энергия системы, а, соответственно, и амплитуда будут возрастать. При отсутствии сопротивления среды амплитуда стремится к бесконечно большим значениям. При
направление вынуждающей силы все время совпадает с направлением перемещения, и, следовательно, вынуждающая сила будет непрерывно совершать положительную работу. Т.о., механическая энергия системы, а, соответственно, и амплитуда будут возрастать. При отсутствии сопротивления среды амплитуда стремится к бесконечно большим значениям. При 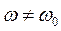 вынуждающая сила на одних перемещениях совершает положительную работу, а на других – отрицательную, и потому амплитуда вынужденных колебаний невелика.
вынуждающая сила на одних перемещениях совершает положительную работу, а на других – отрицательную, и потому амплитуда вынужденных колебаний невелика.


