
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экономическая интерпретация двойственной задачи
Что отражает двойственная модель? Оказывается, она дает возможность оценить решение исходной (прямой) задачи. В рассматриваемом примере прямая задача состоит, фактически, в наилучшем использовании всех имеющихся ресурсов. Каждому варианту плана поизводства продукции соответствует свое использование ресурсов, а, следовательно, и их полезность или значимость. Под последним понимается степень влияния ресурса на результат. Так как каждому условию прямой задачи, отражающему использование ресурса, ставится в соответствие двойственная переменная, то именно она и является мерилом значимости этого ресурса. Действительно, рассмотрим уравнение размерности условия двойственной задачи [A][U]=[C]. Пусть, например, ресурс – фонд времени оборудования (сколько часов оборудование может быть загружено в течение планового периода). Тогда размерность двойственной переменной будет
Итак, U дает стоимость единицы ресурса в единицах критерия, то есть в нашем случае – прирост произведенной стоимости в рублях на каждый дополнительный час работы оборудования. Ниже, в теоремах двойственности, это будет показано строго математически. Поэтому двойственные переменные называют также теневыми ценами. Чтобы увидеть отличие теневой цены от рыночной, возьмем конкретные цифры. Пусть рыночная цена некоторого ресурса, полностью используемого в производстве, равна 500 руб/кг и 1 кг достаточно (при наличии других ресурсов) для выпуска дополнительной продукции на сумму 100000 руб. Тогда теневая цена этого ресурса равна 100000 руб. Если поставщик сорвал поставку данного ресурса, то он должен нести ответственность не в размере рыночной цены, а по теневой цене за каждую единицу недопоставленного ресурса. Такое предложение было высказано впервые Л. Канторовичем, который называл двойственные переменные объективно обусловленными оценками, сокращенно О.О.О. (объективные цены, складывающиеся в конкретной ситуации производства и потребления). Таким образом, чем больше абсолютная величина двойственной переменной, тем выше значимость ресурса в полученном решении, и наоборот, более сильному влиянию ресурса на критерий соответствует большее значение двойственной переменной. Теперь интерпретируем условия двойственной задачи. Если Ui – объективная цена за единицу ресурса, то левая часть неравенства двойственной модели представляет собой полные затраты на производство единицы продукции, а все неравенство отражает тот факт, что произведенная стоимость Ci не может превышать суммарных затрат.
Значимость ресурса эквивалентна его дефицитности. Поэтому критерий двойственной задачи можно интерпретировать как суммарную дефицитность ресурсов, которую следует минимизировать. Другая трактовка заключается в том, что двойственная задача моделирует взаимодоговоренности Покупателя и Продавца ресурсов. Продавец готов продать свои ресурсы, отказавшись от производства продукции, если цены на них (Ui) будут такими, что он получит за ресурсы, расходуемые им на единицу продукции, не меньше Ci, то есть не меньше того, что он имел бы от производства этой продукции. Эти требования выражаются неравенствами двойственной задачи. С другой стороны, Покупатель стремится к таким ценам, которые минимизируют плату за все ресурсы. Это стремление и выражает критерий двойственной задачи. Теоремы двойственности Между решениями прямой и двойственной задач существует тесная взаимосвязь, которая устанавливается теоремами двойственности. Эта связь позволяет по решению одной задачи двойственной пары получать решение другой. Основными являются две теоремы, первая из которых определяет связи критериев, а вторая - условий и переменных. Мы сначала рассмотрим составляющие второй теоремы как самостоятельные теоремы, а затем приведем сводную. Аналогично поступим и с первой основной теоремой двойственности. Теорема 1. Если в оптимальном решении прямой задачи условие выполняется как строгое неравенство
то соответствующая двойственная переменная равна нулю, то есть
Обоснование следует из смысла двойственных переменных. Неравенство (4.32) означает, что i- й ресурс используется не полностью, следовательно, малое изменение этого ресурса не повлияет на результат деятельности (критерий) и поэтому значение двойственной переменной равно нулю. Следствие. Если дополнительная переменная в i- м условии прямой задачи больше нуля, то соответствующая двойственная переменная равна нулю.
Действительно, в этом случае i- е условие без дополнительной переменной будет заведомо строгим неравенством, что и оговорено в теореме.
Теорема 2. Если в единственном оптимальном решении прямой задачи условие выполняется как равенство, то есть
то соответствующая двойственная переменная будет заведомо не равна нулю. Равенство (4.33) означает, что i- й ресурс полностью исчерпан, следовательно, малые изменения этого ресурса обязательно приведут к изменению критерия и поэтому его значимость не равна нулю. Следствие. Если дополнительная переменная в i- м условии равна нулю, то двойственная переменная этого условия не равна нулю.
Случай с неединственным оптимальным решением показан на рис.4.10. Линия оптимального значения критерия L* совпадает с границей по 2-му ресурсу. В оптимальном решении, соответствующем вершине А, первые два ресурса используются полностью. Однако изменение b 1 не приводит к изменению критерия, тогда как любое изменение b 2 отражается на оптимальном значении критерия. Поэтому оценки этих ресурсов разные: U 1 = 0, U 2¹0. Теоремы 1 и 2 легко трансформируются для двойственной задачи. Теорема
Интерпретация: если затраты превышают производимую стоимость, то производить такую продукцию невыгодно. Теорема
Так как производимая стоимость равна затратам, то производство такой продукции окупается. Обобщением рассмотренных теорем является вторая основная теорема двойственности: Для того чтобы векторы X * и U* являлись оптимальными решениями прямой и двойственной задач соответственно, необходимо и достаточно выполнение следующих условий:
Эта теорема учитывает и случай множественности оптимальных решений, когда равенству в одной задаче может сответствовать нулевая переменная в другой. Теперь покажем на конкретном примере, как приведенные теоремы позволяют находить решение одной из задач двойственной пары по известному решению другой. Пример 4.5. Рассмотрим задачу, которая решалась ранее графически и симплекс-методом.
Оптимальное решение этой задачи:
Запишем модель двойственной задачи (ДЗ):
2 U 1+2 U 2+3 U 4³7; 3 U 1+ U 2+3 U 3³5; " Ui ³0. Получим ее решение на основе решения ПЗ и теорем двойственности. Так как дополнительные переменные х5 и х6, входящие в третье и четвертое условия ПЗ, в оптимальном решении не равны нулю, то согласно следствию теоремы 1
Из первой группы условий (4.36) следует, что если исходная переменная ПЗ не равна нулю, то ограничение ДЗ будет выпополняться как равенство. Поэтому в нашем примере имеем:
Получили систему 2-х уравнений с двумя неизвестными. Ее решение:
Таким образом, мы нашли решение ДЗ без применения симплекс-метода. Как увидим ниже, равенство оптимальных значений критериев ПЗ и ДЗ не случайно. Разумеется, таким способом решать ДЗ нецелесообразно, так как в реальных случаях пришлось бы решать систему уравнений большой размерности. Пример только демонстрирует связь решений двойственной пары задач, а значения двойственных переменных легко получить из оптимальной симплекс-таблицы ПЗ. Они расположены в вспомогательной строке Z в столбцах начального базиса. Обратившись к симплекс-таблице 3 в разд.4.9.7, легко убедиться в справедливости этого способа нахождения двойственных переменных (см. в столбцах А 3, А 4, А 5и А 6). Следующая группа теорем определяет связь между критерими двойственной пары задач. Теорема 3. Если X и U – допустимые решения прямой и двойственной задач соответственно, то L( X) £ Доказательство. Так как допустимость решений означает выполнение неравенств
из которой следует справедливость теоремы. Таким образом, для любых допустимых решений значение критерия прямой задачи не может превышать значение критерия двойственной.
Теорема 4. Если X * и U * - допустимые решения прямой и двойственной задач и L (X *)= Доказательство. Согласно теореме 3 для любого допустимого X справедливо неравенство L (X)£ И так как L (X *)= Аналогично доказывается оптимальность U * для двойственной задачи. Теорема 5. Для любых оптимальных X * и U * линейные формы прямой и двойственной задач равны:
L (X *)= Доказательство. В оптимальных решениях выполняются равенства (4.36). Суммируя первую группу по j, а вторую по i и сделав простые преобразования, получаем
Из равенства левых частей следует равенство правых и, значит, справедливость теоремы. Теперь ясно, что совпадение значений критериев в приведенном примере не является случайным. Теорема позволяет строго объяснить смысл двойственных переменных. Действительно, правомерна запись L* =
Таким образом, в оптимальном решении двойственная переменная является производной оптимального значения критерия по правой части ограничения. Значит, как уже говорилось, оптимальная двойственная переменная показывает, как изменится оптимальное значение критерия при изменении ресурса на единицу (она равна этому изменению критерия).
Теорема 6. Если линейная форма одной из задач двойственной пары не ограничена, то условия другой противоречивы. (Обратное не всегда верно, возможна противоречивость в обеих задачах). Доказательство проведем от противного. Допустим, что при неограниченности L (x) сверху в прямой задаче условия двойственной задачи непротиворечивы. Тогда существует допустимое решение ДЗ, на котором. значение ее критерия конечно. Но согдасно теореме 3 для допустимых решений должно выполняться неравенство L (x)£ Аналогично доказывается 2-я часть теоремы для случая неограниченности снизу
Обобщением теорем 3-5 является первая основная теорема двойственности: Если одна из задач двойственной пары разрешима, то и другая задача разрешима, при этом оптимальные значения критериев равны; при неразрешимости одной из задач другая тоже неразрешима.▲
Что дает двойственность для решения задач ЛП помимо анализа? Во-первых, вместо решения исходной задачи можно решать двойственную. Это выгодно, если в ПЗ число условий существенно больше числа переменных (тогда в ДЗ будет меньше ограничений и потребуется меньше итераций). Кроме того, переход к ДЗ может уменьшить число искусственных переменных или исключить их совсем. Во-вторых, теория двойственности породила такие методы как двойственный симплекс-метод и метод сокращения невязок или венгерский метод. В последнем используются неотрицательные оптимальные решения, при которых не выпоняются некоторые ограничения-равенства (имеются невязки), но от итерации к итерации невязки уменьшаются. Нулевые невязки являются признаком достижения допустимого оптимального решения. Метод применяется в основном для решения транспортных задач.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 520; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.138.144 (0.03 с.) |
 .
. , (4.32)
, (4.32)
 (4.33)
(4.33)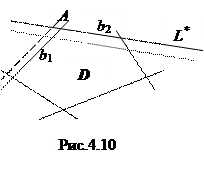
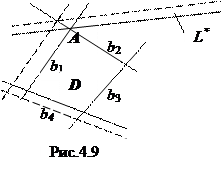 На рис.4.9 приведена геометрическая интерпретация рассмотренных теорем для случая единственного оптимального решения (вершина А). Здесь допустимое множество D образовано четырьмя условиями- неравенствами с ресурсами b 1, b 2, b 3 и b4. В оптимальном решении по 1-му и 2-му ресурсам выполняется равенство и изменение любого из них (показано пунктиром для b 1)приводит к перемещению оптимальной вершины и, следовательно, критерия. Поэтому значимость этих ресурсов или их двойственные переменные отличны от нуля. В то же время по 3-му и 4-му ресурсам имеем строгие неравенства и их изменения не влияют на оптимальное значение критерия, что соответствует нулевым дополнительным переменным.
На рис.4.9 приведена геометрическая интерпретация рассмотренных теорем для случая единственного оптимального решения (вершина А). Здесь допустимое множество D образовано четырьмя условиями- неравенствами с ресурсами b 1, b 2, b 3 и b4. В оптимальном решении по 1-му и 2-му ресурсам выполняется равенство и изменение любого из них (показано пунктиром для b 1)приводит к перемещению оптимальной вершины и, следовательно, критерия. Поэтому значимость этих ресурсов или их двойственные переменные отличны от нуля. В то же время по 3-му и 4-му ресурсам имеем строгие неравенства и их изменения не влияют на оптимальное значение критерия, что соответствует нулевым дополнительным переменным. . Если в оптимальном решении двойственной задачи условие выполняется как строгое неравенство
. Если в оптимальном решении двойственной задачи условие выполняется как строгое неравенство (4.34)
(4.34)

 Если в единственном оптимальном решении двойственной задачи условие выполняется как равенство, то соответствующая переменная прямой задачи строго больше нуля:
Если в единственном оптимальном решении двойственной задачи условие выполняется как равенство, то соответствующая переменная прямой задачи строго больше нуля: . (4.35)
. (4.35) (4.36)
(4.36)



 =19 U 1+13 U 2+12 U 3+17 U 4®miin;
=19 U 1+13 U 2+12 U 3+17 U 4®miin; .
.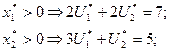

 .
. в ПЗ и
в ПЗ и  в ДЗ, то очевидна цепочка соотношений
в ДЗ, то очевидна цепочка соотношений
 (U *). (4.38)
(U *). (4.38)
 . Отсюда имеем
. Отсюда имеем (4.39)
(4.39)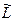 (U), что при принятом допущении невозможно (L бесконечно, а
(U), что при принятом допущении невозможно (L бесконечно, а 


