
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Контрольная работа № 2. «введение в анализ. Дифференциальное исчисление».
1. Найти пределы функций. 1. 1) 2) 2. 1) 2) 3. 1) 2) 4. 1) 2) 5. 1) 2) 6. 1) 2) 7. 1) 2) 8. 1) 2) 9. 1) 2) 10. 1) 2) 2. Найти производные заданных функций. 1. 1) 2. 1) 3) 3. 1) 3) 4. 1) 3) 5. 1) 3) 6. 1) 3) 7. 1) 3) 8. 1) 3) 9. 1) 3) 10. 1) 3) 3. Провести полное исследование функции и построить ее график. 1. 3. 5. 7. 9. 4. Доказать, что функция z = f (x; y) удовлетворяет данному уравнению. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Основные теоретические сведения. Теория пределов Основные понятия 1. Постоянное число l есть предел функции y = f (х): 2. Если существует 3. Функция a(x) называется бесконечно малой функцией при х → а, если 4. Если a(x) – бесконечно малая функцией при х → а, то Основные теоремы о действиях над функциями, 5. Пусть 1) 2) 3) 4) 5) Если n – натуральное число, то 6) Если n – натуральное число, то 7) Правило замены переменной. Пусть требуется найти предел сложной функции y = f (j(x)) при x → a. Тогда если существует Важные исключения из теоремы 6) Если 7) Если 8) Если
Существуют и другие виды неопределенностей. Замечательные пределы 9) Первый замечательный предел: 10) Основные следствия из первого замечательного предела: 1) 3) 5) 7) 9) 11) 13) 15) 11) Второй замечательный предел: 12) Основные следствия из второго замечательного предела: 1) 3) 5) 7) 9) 11) 13) 15) 17) Дифференциальное исчисление функций одной переменной 1. Производной функции Таблица производных 2. 4. 6. 8. 10. 12. 14. 16. Основные правила дифференцирования 17. 19. 21. Геометрический смысл производной 22. Производная от функции
Рис. 7 Механический смысл производной 23. Производная от функции 24. Если функция задана параметрически уравнениями 25. Если функция задана неявно уравнением Применение производной 26. Если на некотором промежутке 27. Если функция 28. Если на некотором промежутке 29. Если функция 30. Для нахождения наибольшего или наименьшего значения функции а) найти критические точки – точки, в которых производная функции
б) найти значения функции в критических точках, принадлежащие отрезку в) выбрать среди полученных чисел наибольшее или наименьшее. 31. Для исследования функции а) определяется область определения функции, находятся точки разрыва, определяется их характер, находятся вертикальные асимптоты, если они есть; б) проверяется четность, нечетность, периодичность графика, поведение его при в) находится производная г) находится вторая производная д) если необходимо, находятся дополнительные точки. Сведя всю полученную информацию в таблицу, строят график функции
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.156.35 (0.072 с.) |
 при: а)
при: а)  ; б)
; б)  ; в)
; в) 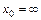 ;
; ; 3)
; 3)  .
. при: а)
при: а)  ; б)
; б)  ; 3)
; 3)  .
. при: а)
при: а)  ; в)
; в)  ; 3)
; 3)  .
. при: а)
при: а)  ; в)
; в) 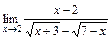 ; 3)
; 3)  .
. при: а)
при: а) 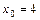 ; в)
; в)  ; 3)
; 3)  .
.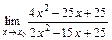 при: а)
при: а) 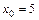 ; в)
; в) 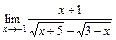 ; 3)
; 3) 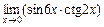 .
. при: а)
при: а)  ; б)
; б)  ; в)
; в) 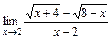 ; 3)
; 3)  .
. при: а)
при: а)  ; в)
; в)  ; 3)
; 3)  .
. при: а)
при: а) 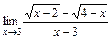 ; 3)
; 3)  .
.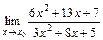 при: а)
при: а)  ; в)
; в)  ; 3)
; 3) 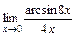 .
. ; 2)
; 2) 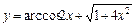 ;
; .
.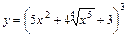 ; 2)
; 2)  ;
; .
. ; 2)
; 2)  ;
;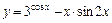 .
. ; 2)
; 2)  ;
; .
.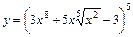 ; 2)
; 2)  ;
;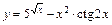 .
. ; 2)
; 2)  ;
; .
. ; 2)
; 2) 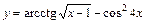 ;
; .
. ; 2)
; 2)  ;
; .
. ; 2)
; 2) 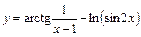 ;
; .
. ; 2)
; 2)  ;
;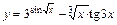 .
. . 2.
. 2. 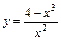 .
. . 4.
. 4.  .
.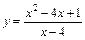 . 6.
. 6.  .
. . 8.
. 8.  .
. . 10.
. 10.  .
. , если
, если  .
.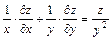 , если
, если 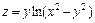 .
. , если
, если 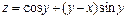 .
. , если
, если 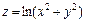 .
. , если
, если  .
. , если
, если  .
. , если
, если 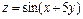 .
. , если
, если 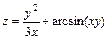 .
. , если
, если 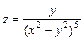 .
. , если
, если 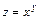 .
.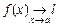 или
или  , если для любого сколь угодно малого числа e > 0 существует число d > 0, зависящее от e такое, что из выполнения неравенства
, если для любого сколь угодно малого числа e > 0 существует число d > 0, зависящее от e такое, что из выполнения неравенства 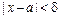 следует неравенство
следует неравенство 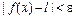 .
. . Аналогично, если существует
. Аналогично, если существует  . Эти пределы называются односторонними пределами.
. Эти пределы называются односторонними пределами. . Аналогично, функция b(х) называется бесконечно большой при х → а, если
. Аналогично, функция b(х) называется бесконечно большой при х → а, если  .
.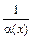 – бесконечно большая функция при х → а; если b(x) – бесконечно большая функцией при х → а, то
– бесконечно большая функция при х → а; если b(x) – бесконечно большая функцией при х → а, то  – бесконечно малая функция при х → а.
– бесконечно малая функция при х → а. ,
, 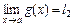 , где l 1, l 2 – конечные, тогда:
, где l 1, l 2 – конечные, тогда: ;
;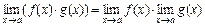 ;
; при
при  ;
; ;
; ;
; ;
; и существует
и существует 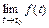 , то справедлива формула
, то справедлива формула 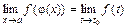 .
. и
и  , то частное
, то частное  при x → a называется неопределенностью вида
при x → a называется неопределенностью вида  .
.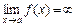 и
и  , то разность f (x) – g (x) при x → a называется неопределенностью вида (¥ – ¥), а частное
, то разность f (x) – g (x) при x → a называется неопределенностью вида (¥ – ¥), а частное  .
. .
. ; 2)
; 2) 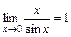 ;
; ; 4)
; 4)  ;
;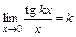 ; 6)
; 6) 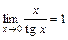 ;
; ; 8)
; 8)  ;
;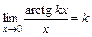 ; 10)
; 10)  ;
; ; 12)
; 12)  ;
; ; 14)
; 14) 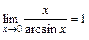 ;
; .
. .
. ; 2)
; 2)  ;
;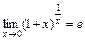 ; 4)
; 4)  ;
; ; 6)
; 6) 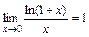 ;
; ; 8)
; 8)  ;
; ; 10)
; 10)  ;
; ; 12)
; 12)  ;
; ; 14)
; 14)  ;
;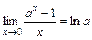 ; 16)
; 16)  ;
; .
.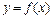 в точке x 0 называется предел отношения приращения функции в точке x 0 к приращению аргумента D x, когда
в точке x 0 называется предел отношения приращения функции в точке x 0 к приращению аргумента D x, когда  , т. е.
, т. е.  .
. . 3.
. 3. 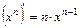 .
. . 5.
. 5.  .
. . 7.
. 7. 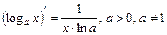 .
. . 9.
. 9.  .
. . 11.
. 11.  .
.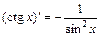 . 13.
. 13.  .
.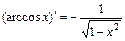 . 15.
. 15.  .
. .
.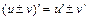 . 18.
. 18.  .
. . 20.
. 20.  .
.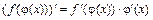 .
. в точке
в точке  равна угловому коэффициенту (т. е. тангенсу угла наклона) касательной, проведенной к графику функции
равна угловому коэффициенту (т. е. тангенсу угла наклона) касательной, проведенной к графику функции  (рис. 7). Уравнение касательной:
(рис. 7). Уравнение касательной: 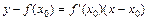 . Уравнение нормали:
. Уравнение нормали: 

 .
. то производная вычисляется по формуле:
то производная вычисляется по формуле:  . Вторая производная находится по формуле:
. Вторая производная находится по формуле:  .
.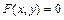 , то для нахождения ее производной дифференцируют обе части этого уравнения, считая
, то для нахождения ее производной дифференцируют обе части этого уравнения, считая  сложной функцией от
сложной функцией от  и полученное уравнение разрешают относительно
и полученное уравнение разрешают относительно  .
.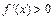 , то на этом промежутке функция
, то на этом промежутке функция  возрастает; если
возрастает; если 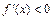 , то функция убывает.
, то функция убывает. непрерывна в точке
непрерывна в точке  и в левой ее окрестности
и в левой ее окрестности  , то на этом промежутке функция
, то на этом промежутке функция 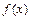 вогнута; если
вогнута; если  , то функция выпукла.
, то функция выпукла. нужно:
нужно: , не существует или равна бесконечности;
, не существует или равна бесконечности; и построения ее графика пользуются следующей схемой:
и построения ее графика пользуются следующей схемой: (или на границах области определения, если она ограничена); определяется наличие невертикальных асимптот вида
(или на границах области определения, если она ограничена); определяется наличие невертикальных асимптот вида  , для чего числа k и b находятся по формулам:
, для чего числа k и b находятся по формулам:  ,
,  , если оба эти предела существуют и конечны;
, если оба эти предела существуют и конечны; , определяются интервалы возрастания
, определяются интервалы возрастания 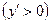 , убывания
, убывания  и критические точки (
и критические точки ( или не существует) функции, находятся экстремумы;
или не существует) функции, находятся экстремумы; , определяются интервалы выпуклости вверх
, определяются интервалы выпуклости вверх  , выпуклости вниз
, выпуклости вниз  и точки перегиба графика;
и точки перегиба графика;


