
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Затухающие колебания и их характеристики
С в о б о д н ы е к о л е б а н и я р е а л ь н ы х с и с т е м в с е г д а з а т у х а ю т, так как часть первоначальной энергии системы тратится на работу против сил сопротивления в механических системах и на джоулево тепло - в электрических системах. Рассмотрим свободные затухающие колебания пружинного маятника. Действующую на него силу сопротивления
где r - коэффициент сопротивления, зависящий от вязкости среды, размеров и формы тела; минус говорит о том, что сила С учетом силы сопротивления II закон Ньютона для груза имеет вид
Разделим его на m и введем обозначения
Тогда дифференциальное уравнение свободных затухающих колебаний маятника запишется в виде
где Следуя общим правилам решения линейных дифференциальных уравнений с постоянными коэффициентами, полагаем
Общее решение уравнения (30)
где Здесь следует различать два случая. Если
Учитывая (1а),затухающие колебания будут описываться функцией
где
не повторяются. Однако можно говорить об условной циклической частоте затухающих колебаний
Энергия системы
где Второй случай реализуется, если
описывает апериодическое движение,при котором Характеристики затухающих колебаний В р е м я р е л а к с а ц и и
Отсюда следует, что
За время релаксации система успевает совершить число колебаний, равное
Л о г а р и ф м и ч е с к и й д е к р е м е н т к о л е б а н и й
Практически логарифмический декремент определяется по формуле
Д о б р о т н о с т ь Q - равна отношению энергии системы Е(t) в момент времени t к убыли этой энергии за один последующий период затухающих колебаний, умноженному на
Учитывая (35)
При малых значениях логарифмического декремента
Вынужденные колебания В ы н у ж д е н н ы е к о л е б а н и я в о з н и к а ю т п р и в н е ш н е м п е р и о д и ч е с к о м в о з д е й с т в и и н а к о л е б а т е л ь н у ю с и с т е м у. Общей чертой вынужденных колебаний является то,что спустя некоторое время система полностью «забывает» свое начальное состояние,и в ней устанавливаются незатухающие колебания с частотой внешнего воздействия. Рассмотрим вынужденные колебания на примере механической системы (рис.14). Маятник в виде заряженного шарика на длинном стержне из диэлектрика помещен между вертикальными пластинами плоского конденсатора, на которые подается переменное напряжение. Если внешняя сила
то уравнение движения для маятника имеет вид
Введя обозначения
Решением такого уравнения является сумма общего решения однородного уравнения
где первый член описывает свободные затухающие колебания, второй - незатухающие колебания с частотой Через время, равное времени релаксации
Из этого следует, что
Подставим:
(1) (2) (3) (4) Проведем сложение трех гармонических колебаний в левой части уравнения методом векторных диаграмм. Для этого произвольно расположим вектор
Резонанс Кривая, описывающая зависимость амплитуды вынужденных колебаний от частоты внешнего воздействия W, называется резонансной кривой или амплитудно - частотной характеристикой (АЧХ). П р и п р и б л и ж е н и и ч а с т о т ы в н е ш н е й с и л ы W к ч а с т о т е w0 н а б л ю д а е т с я в о з р а с т а н и е а м п л и т у д ы в ы н у ж д е н н ы х к о л е б а н и й. Э т о я в л е н и е н а з ы в а е т с я р е з о н а н с о м. Рассмотрим физическую сторону этого явления в разных областях частот. Если W<<w0, первый и второй члены в уравнении малы по сравнению с третьим и уравнение движения сводится к виду
В этом случае внешняя сила «идет» на преодоление квазиупругой силы, и колебания будут происходить со статической амплитудой
Если W>>w0, первый член в левой части уравнения много больше остальных и уравнение движения будет иметь вид
Решение его В области резонанса
Таким образом, в условиях резонанса роль внешней силы сводится главным образом к компенсации действующих в механической системе сил трения и ускорение создается силой упругости. При этом система совершает почти «гармонические» колебания с максимальной для нее амплитудой
Значение р е з о н а н с н о й ч а с т о т ы WРЕЗ можно определить из условия минимальности знаменателя в выражении
При d<<w0 , Отсюда следует, что чем выше добротность системы Q, тем острее «резонансный пик» (рис. Поскольку энергия осциллятора пропорциональна квадрату амплитуды, при резонансе система обладает наибольшей энергией ЕРЕЗ. Пусть
Чтобы убедится в справедливости, составим соотношение
Так как то отсюда
ВОЛНЫ Ф р о н т в о л н ы - геометрическое место точек системы, до которых доходят колебания источника к моменту времени t. Фронт волны представляет ту поверхность, которая отделяет часть системы, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли. Геометрическое место точек, в которых колебания совершаются в одинаковой фазе, называется в о л н о в о й п о в е р х н о с т ь ю. Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости - п л о с к а я в о л н а, или форму сферы - с ф е р и ч е с к а я в о л н а. Волну можно считать сферической на расстояниях значительно превышающих размеры источника (точечный источник) и при условии, что скорость распространения возмущения одинакова по всем направлениям (изотропная среда). Если источник возмущения находится настолько далеко, что волновая поверхность представляет собой плоскость (сфера очень большого радиуса), то говорят о плоской волне. Волна называется п о п е р е ч н о й, если колебания совершаются в направлениях, перпендикулярных к направлению распространения волны. Волна называется п р о д о л ь н о й, если колебания происходят в направлении распространения волны.
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 214; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.83.150 (0.023 с.) |
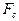 при малых скоростях движения груза можно считать пропорциональной скорости
при малых скоростях движения груза можно считать пропорциональной скорости 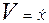
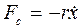 .
.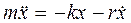 .
.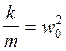 ;
; 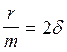 .
.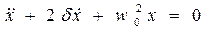 ,
,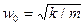 собственная частота,а
собственная частота,а 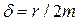 называется коэффициентом затухания.
называется коэффициентом затухания.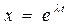 и находим для
и находим для 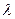 характеристическое уравнение
характеристическое уравнение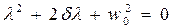 .
.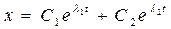 ,
,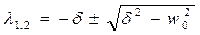 .
.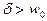 , то имеем два комплексно сопряженных значения
, то имеем два комплексно сопряженных значения 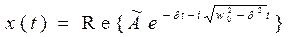 .
.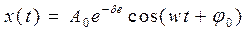 ,
,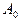 - начальная амплитуда;
- начальная амплитуда; 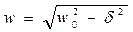 ;
; 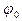 - начальная фаза. График зависимости
- начальная фаза. График зависимости 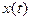 изображен на рис. Строго говоря, з а т у х а ю щ и е к о л е б а н и я н е я в л я ю т с я п е р и о д и ч е с к и м и, так как значение амплитуды
изображен на рис. Строго говоря, з а т у х а ю щ и е к о л е б а н и я н е я в л я ю т с я п е р и о д и ч е с к и м и, так как значение амплитуды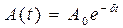
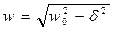 и об условном периоде
и об условном периоде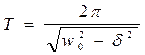 .
.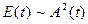 при условии
при условии 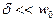 в среднем за период убывает по закону
в среднем за период убывает по закону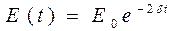 ,
,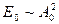 - начальное значение энергии.
- начальное значение энергии.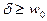 . При этом оба значения
. При этом оба значения 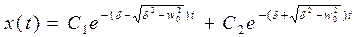
 убывает,если
убывает,если  .
.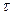 - время, в течении которого амплитуда свободных колебаний убывает в е раз, то есть
- время, в течении которого амплитуда свободных колебаний убывает в е раз, то есть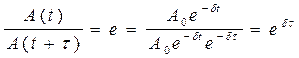 .
.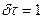 или
или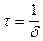 .
.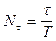 .
.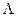 показывает, какую долю период составляет от времени релаксации и, таким образом, обратен по величине числу колебаний
показывает, какую долю период составляет от времени релаксации и, таким образом, обратен по величине числу колебаний 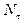 :
: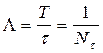 .
.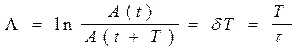 .
.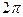
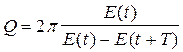 .
.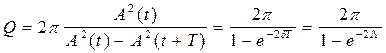 .
.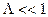
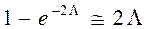 и
и 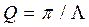 .
. изменяется гармонически с частотой
изменяется гармонически с частотой  и амплитудой
и амплитудой 
 ,
, .
.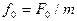 , получим линейное неоднородное дифференциальное уравнение вынужденных колебаний
, получим линейное неоднородное дифференциальное уравнение вынужденных колебаний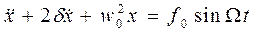 .
. и частного решения неоднородного уравнения
и частного решения неоднородного уравнения ,
, между действием силы и смещением х.
между действием силы и смещением х. .
. ,
, .
. .
. , описывающий третье колебание. Вектор
, описывающий третье колебание. Вектор  , описывающий первое колебание, опережает его на p, а вектор
, описывающий первое колебание, опережает его на p, а вектор  - на p/2. Так как сумма
- на p/2. Так как сумма  , из рисунка следует
, из рисунка следует ;
; .
. .
. .
. .
. будет описывать колебания с амплитудой
будет описывать колебания с амплитудой  , при которых силы трения и упругости становятся несущественными по сравнению с внешней силой. При W ® ¥ амплитуда колебания А стремится к нулю.
, при которых силы трения и упругости становятся несущественными по сравнению с внешней силой. При W ® ¥ амплитуда колебания А стремится к нулю. первый и третий члены уравнения (51) сравняются, а так как они противоположны по знаку, то
первый и третий члены уравнения (51) сравняются, а так как они противоположны по знаку, то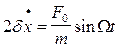 ,
,  .
. .
. ,
, .
. и
и  , а с учетом
, а с учетом 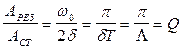 .
. и
и  - циклические частоты, при которых энергия системы убывает в два раза по сравнению с
- циклические частоты, при которых энергия системы убывает в два раза по сравнению с  ,тогда величина
,тогда величина 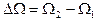 называется шириной резонансной кривой. Для системы с высокой добротностью
называется шириной резонансной кривой. Для системы с высокой добротностью  ;
;  и
и .
. .
. ,а
,а  ,
, ,
, . С учетом можно получить очень важное соотношение между полушириной резонансной кривой
. С учетом можно получить очень важное соотношение между полушириной резонансной кривой 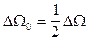 вынужденных колебаний и временем релаксации свободных затухающих колебаний:
вынужденных колебаний и временем релаксации свободных затухающих колебаний: .
.


