
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Лагранжа (о конечных приращениях).Стр 1 из 3Следующая ⇒
Теорема Лагранжа (о конечных приращениях). Пусть функция y = f (x) 1) непрерывна на отрезке [a;b]; 2) дифференцируема на интервале (a;b). Тогда на интервале (a;b) найдется по крайней мере одна точка такая, что ◄Введем вспомогательную функцию L(x) на отрезке [a;b], определив ее так: L(x)= f(x) - f(a) - 1) она непрерывна на [a;b], поскольку непрерывны все слагаемые L(x); 2) на (a;b) функция L(x)имеет производную; 3) L(a) = L(b) = 0. Из теоремы Ролля следует, что существует точка x0∈(a;b), в которой L′ (x) = 0. Следовательно, L’(x)= f’(x0) - Геометрический смысл теоремы Лагранжа. Отношение
Теорема Коши (об отношении конечных приращений двух Функций). Если функции y = f (x) и y = g (x) 1) непрерывны на отрезке [a;b]; 2) дифференцируемы на интервале (a; b); 3) производная g ′ (x) ≠ 0 на интервале (a; b). Тогда на интервале (a; b) найдется по крайней мере одна точка x0 такая, что ◄Из условия теоремы следует, что g ′ (x) ≠ 0. Это означает, что разность g (b) − g (a) ≠ 0. Действительно, если бы g (b) − g (a) = 0, то функция y=g(x), являясь непрерывной и дифференцируемой, удовлетворяла бы условиям теоремы Ролля и в таком случае g′(x) была бы равна нулю по крайней мере в одной точке x0 интервала (a; b), что противоречит условию. Введем вспомогательную Функцию K(x) =f(x) - f(a) - Эта функция удовлетворяет всем условиям теоремы Ролля: 1) K(x) непрерывна на отрезке [a;b], так как непрерывны функции у=f(x) и y=g(x); 2) функция K(x) имеет производную всюду в интервале (a; b), поскольку каждое слагаемое в правой части функции K(x) имеет производную на этом интервале; 3) K(a) = K(b) = 0, в чем убеждаемся непосредственной проверкой. Из теоремы Ролля делаем вывод о существовании точки x0, что K '(x0)= 0. Поэтому K’(x) =f’(x0) - Теорема Лагранжа является частным случаем теоремы Коши: достаточно в теореме Коши взять g (x) = x.
Теорема Лопиталя (нахождения предела отношения Функций через предел отношения их производных). Пусть функции y = f(x) и y = g (x) 1) дифференцируемы в окрестности точки a, кроме, быть может, самой точки a; 2) g (x) ≠ 0 и g ′(x) ≠ 0 в этой окрестности; 3) lim(x→a) f(x)= 0,; lim(x→a) g(x)= 0 4) существует lim(x→a) Тогда существует lim(x→a) ◄В теореме ничего не сказано о значениях y = f(x) и y = g (x) в точке х=а. Положим f(a) = g(a) = 0. Так как теперь lim(x→a)f(x)=f(a) и lim(x→a)g(x)=g(a), то функции y = f(x) и y = g (x) будут непрерывны в точке а. Поэтому на отрезке [a;x], где х - какая угодно точка окрестности точки а, функции y = f(x) и y = g (x) удовлетворяют всем условиям теоремы Коши. Следовательно,между а и х найдется по крайней мере одна точка такая, что и lim(x→a) Последнее равенство выражает правило Лопиталя, по которому вычисление предела отношения двух функций может быть заменено при выполнении условий теоремы вычислением предела отношения производных этих функций. Это один из наиболее мощных методов нахождения пределов. Признаки монотонности ф-ии Теорема. (Достаточное условие возрастания (убывания) функции на интервале Х). Пусть функция f(x) 1) определена на интервале Х; 2) имеет на Х конечную производную f '(x); 3) f '(x)>0 (f '(x)<0) на Х. Тогда f(x) является возрастающей (убывающей) на интервале Х. Доказательство. Рассмотрим случай, когда f '(x)<0 на Х. Возьмем любые два значения х1 и х2 из Х такие, что х1 < х2, тогда на сегменте [х1, х2] f(x) удовлетворяет всем условиям теоремы Лагранжа, поэтому справедливо равенство Для случаев f '(x) >0 на Х доказательство проводится аналогично.
Асимптоты графика функции Прямая x = x 0 называется вертикальной асимптотой графика функции y=f(x), если хотя бы одно из предельных значений lim x → x −0 f(x) или lim x → x +0 f(x) равно + ∞ или − ∞.
Прямая y = y0 называется горизонтальной асимптотой графика функции y=f(x), если хотя бы одно из предельных значений lim x →+∞ f (x)или lim x →-∞ f (x)равно b. График функции может иметь только правую горизонтальную асимптоту или только левую. Прямая y = kx + b называется наклонной асимптотой графика функции y=f(x), если lim x →+∞(f(x)-kx-b)= 0, т.е. когда функция при x →∞ представима в виде f (x) = kx + b +α(x), где lim x →+∞α(x) = 0. Существование асимптоты y = kx + b у кривой y=f(x) при x →∞ означает, что при x →∞ функция ведет себя «почти как линейная», т. е. отличается от линейной функции y = kx + b бесконечно мало. Наклонная асимптота может быть как правой так и левой. Теорема (об условиях существования наклонной асимптоты) Если для функции y = f (x) существуют пределы lim x →∞
Таблица интегралов 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) 14) 15) 16) 17)
Общие методы интегрирования Наиболее важными методами интегрирования являются: 1) метод непосредственного интегрирования (метод разложения), 2) метод подстановки (метод введения новой переменной), 3) метод интегрирования по частям. I. Метод непосредственного интегрирования Задача нахождения неопределенных интегралов от многих функций решается методом сведения их к одному из табличных интегралов. II. Метод подстановки (интегрирование заменой переменной) Если функция x=φ(t) имеет непрерывную производную, то в данном неопределенном интеграле ∫f(x)dx всегда можно перейти к новой переменной t по формуле: ∫f(x)dx=∫f(φ(t))φ'(t)dt. Затем найти интеграл из правой части и вернуться к исходной переменной. При этом, интеграл стоящий в правой части данного равенства может оказаться проще интеграла, стоящего в левой части этого равенства, или даже табличным. Такой способ нахождения интеграла называется методом замены переменной. III. Метод интегрирования по частям Метод интегрирование по частям основан на следующей формуле: ∫udv=uv-∫vdu, где u(x),v(x) –непрерывно дифференцируемые функции. Формула называется формулой интегрирования по частям. Данная формула показывает, что интеграл ∫udv приводит к интегралу ∫vdu, который может оказаться более простым, чем исходный, или даже табличным.
Ньютона-Лейбница(док-во) Т: Если ВЫВОД ФОРМУЛЫ: Рассм-м
Подставим верхнюю границу:
Задача Коши. Дифференциальное уравнение 1–го порядка имеет бесконечно много решений. Для того чтобы выделить единственное решение, нужно задать дополнительные (начальные) условия. Задача отыскания решения y = y(x) уравнения F(x, y, y ') = 0, удовлетворяющего условию y(x0) = y0, называется задачей Коши (или начальной задачей). Условие y(x0) = y0 — начальное условие.
Гармонический ряд Ряд вида
Обобщенный гармонический ряд, или ряд Дирихле – это ряд вида
Ряд
34. Достаточные признаки сходимости знакоположительных числовых рядов Числовой ряд называется знакоположительным, если un >0 при всех n =1,2,3…. Для таких рядов частичные суммы S1, S2, …, Sn,… образуют возрастающую числовую последовательность S1 < S2 <…< Sn <…. Признак сравнения числовых рядов Пусть даны два знакоположительных числовых ряда причём 0<a n≤bn при любых n =1,2,…. Тогда: 1. Если ряд 2. Если ряд В качестве эталонного числ ряда использ ряд вида Предельный признак сравнения Пусть даны два знакоположительных числовых ряда 35. Признак Даламбера Пусть дан знакоположительный числовой ряд и пусть существует предел Признак Коши Пусть дан знакоположительный числовой ряд При l <1 ряд сходится, при l >1 ряд расходится. При l =1 критерий Коши не позволяет определить сходимость/расходимость Интегральный признак (признак Маклорена-Коши) Пусть задан ряд, непрер ф-я y=f(x) на [1;∞) такая что f(n)=an. Тогда интеграл
35. Знакопеременные ряды Числ ряд наз знакомеременным, если его члены либо положит либо отрицат Признак Коши сходимости знакоперем рядов Числ ряд Если числ ряд Теорема. Из абсолютной сходимоти числ ряда след сходимость исходного ряда, т.е. если Числовой ряд вида u1-u2+u3-u4+…+ … +(- 1 )n- 1. un+ …, где un – модуль члена ряда, называется знакочередующимся числовым рядом, т.е. ряд в к-м члены попеременно меняют знак. Признак Лейбница Если для знакочередующегося числового ряда Выполняются два условия:
1. Члены ряда убывают по модулю u1 > u2 >…> un >…, 2. то ряд (19) сходится, причём его сумма положительна и не превосходит первого члена ряда. Следствие. Остаток ряда Лейбница имеет знак своего первого члена и меньше его по абсолютной величине, т.е.
36. Знакопеременные ряды. Абсолютная и условная сходимость. Числовой овой ряд Если ряд, сост из абсол значений величин Теорема: Если ряд явл абсол сх-ся, то исх ряд сх-ся. Док-во:восп-ся 1 признаком сравнения Рассм-м ряд
О. Если ряд, образ из абсол значений его величин расх-ся, а исх ряд сх-ся, то он наз условно сх-ся. Признак Лейбница Если для знакочередующегося числового ряда Выполняются два условия: 1. Члены ряда убывают по модулю u1 > u2 >…> un >…, 2. то ряд (19) сходится, причём его сумма положительна и не превосходит первого члена ряда. Следствие. Остаток ряда Лейбница имеет знак своего первого члена и меньше его по абсолютной величине, т.е. Если в знакочередующемся ряде члены ряда монотонно убывают по абсолютным значениям и imUn=0 (nà∞), то ряд сходится. Дано: U1>U2>U3>...; imUn=0 (nà∞); U1-U2+U3-U4+..., Ui>0 Доказательство: S2n ¾ чётная частичная сумма: S2n=+U1-U2+U3-U4+...-U2n; S2n=(U1-U2)+(U3-U4)+...+(U2n-1-U2n); S2n>0 ¾ возрастает. S2n=U1-(U2-U3)-(U4-U5)-...-U2n; S2n<U1, U1>0; imS2n=S {nà∞} imS2n+1 {nà∞} = im(S2n+U2n+1)=S; Чётные и нечётные суммы с одним пределом => ряд сходится. 1) Заметим, что S>0, т.е. знак суммы совпадает со знаком первого члена. 2) S<U1
38. Абсол и условная сходимость. О. Ряд вида наз знакочеред-ся. Признак Лейбница (сх-ть знакочер ряда). Для того, чтобы ряд (1) сх-ся достаточно, чтобы абсол значения убывали и →0 при возрастании n, т.е. О. Если ряд, сост из абсол значений величин Теорема: Если ряд явл абсол сх-ся, то исх ряд сх-ся. Док-во:восп-ся 1 признаком сравнения Рассм-м ряд Доказана сх-ть по 2-му признаку сравнения, след-но исх ряд сх-ся абсолютно. О. Если ряд, образ из абсол значений его величин расх-ся, а исх ряд сх-ся, то он наз условно сх-ся.
39. Понятие степенного ряда. Область сходимости степенного ряда. Теорема Абеля. Ряд вида
40. Радиус сходимости и область сходимости степенных рядов. Дифференцирование и интегрирование степенных рядов Свойства степенных рядов 1. Сумма степенного ряда f(x) непрерывна внутри его интервала сходимости 2. Степенной ряд можно почленно интегрировать на любом отрезке целиком принадлежащем интервалу сходимости. Степенной ряд можно почленно дифференцировать в интервале сходимости любое число раз. Ряды полученные почленным интегрированием и почленным дифференцированием степенного ряда имеют тот же радиус сходимости что и исходный ряд. 3. Пусть задан СР 4. Для любого интеграла (α,β)
Теорема Лагранжа (о конечных приращениях). Пусть функция y = f (x) 1) непрерывна на отрезке [a;b]; 2) дифференцируема на интервале (a;b). Тогда на интервале (a;b) найдется по крайней мере одна точка такая, что ◄Введем вспомогательную функцию L(x) на отрезке [a;b], определив ее так: L(x)= f(x) - f(a) - 1) она непрерывна на [a;b], поскольку непрерывны все слагаемые L(x); 2) на (a;b) функция L(x)имеет производную; 3) L(a) = L(b) = 0. Из теоремы Ролля следует, что существует точка x0∈(a;b), в которой L′ (x) = 0. Следовательно, L’(x)= f’(x0) - Геометрический смысл теоремы Лагранжа. Отношение
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 1390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.213.209 (0.119 с.) |
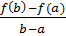 = f’(x0)
= f’(x0)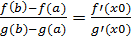
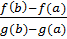 (g(x) - g(a))
(g(x) - g(a))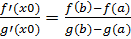 ►
►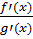 (конеч. или беск.)
(конеч. или беск.)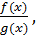 причем lim(x→a)
причем lim(x→a) 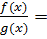 lim(x→a)
lim(x→a) 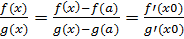 Величина x0 зависит от х, причем x → a при точка x0 также будет стремиться к а. Поэтому lim(x→a)
Величина x0 зависит от х, причем x → a при точка x0 также будет стремиться к а. Поэтому lim(x→a) 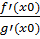
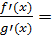 lim(x→a)
lim(x→a) 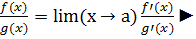
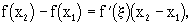 где
где 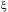 - некоторая точка из (х1, х2): х1<
- некоторая точка из (х1, х2): х1< 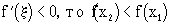 , что означает убывание функции на множестве Х.
, что означает убывание функции на множестве Х. и lim x →∞
и lim x →∞  , то функция имеет наклонную асимптоту y = kx + b при x →∞.
, то функция имеет наклонную асимптоту y = kx + b при x →∞.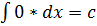
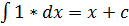
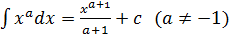
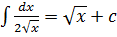
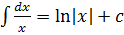
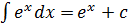
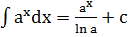
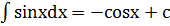
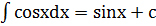
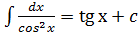
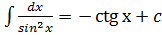
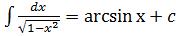 |x|<1
|x|<1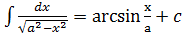 |x|<|a|, a
|x|<|a|, a 
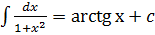 = -arcctgx+c
= -arcctgx+c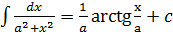 =
= 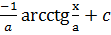
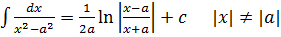
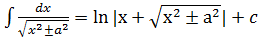
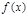 непрерывна на
непрерывна на 
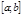 , справедлива ф-ла Ньютона-Лейбница:
, справедлива ф-ла Ньютона-Лейбница: 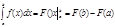
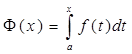 , т.к.
, т.к. 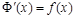 , то
, то 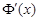 - первообразная для
- первообразная для 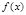 . Но
. Но 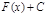 , также первообразная. Это значит что имеет место следующее равенство:
, также первообразная. Это значит что имеет место следующее равенство: 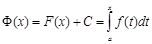
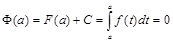
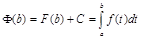
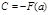 подставами вместо
подставами вместо 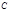 :
: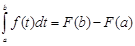 в силу 1-го свойства, что значении определенного интеграла независит от обозначения переменной интегрирования, запишем:
в силу 1-го свойства, что значении определенного интеграла независит от обозначения переменной интегрирования, запишем: 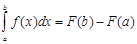
 называется гармоническим. Можно строго сказать, что он расходится.
называется гармоническим. Можно строго сказать, что он расходится. , где α – любое действительное число.
, где α – любое действительное число.

 сходится, то сходится и ряд
сходится, то сходится и ряд 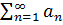 ; из сходимости ряда с большими членами следует сходимость ряда с меньшими членами
; из сходимости ряда с большими членами следует сходимость ряда с меньшими членами расходится, то расходится и ряд
расходится, то расходится и ряд  ≠0, то ряды сходятся или расходятся одновременно. В качестве этал – ряд Дирихле.
≠0, то ряды сходятся или расходятся одновременно. В качестве этал – ряд Дирихле.
 . При l <1 ряд сходится, при l >1 ряд расходится. Если l =1, то признак не дает ответ
. При l <1 ряд сходится, при l >1 ряд расходится. Если l =1, то признак не дает ответ


 (19)
(19)

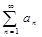 , содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, наз-ся знакопеременным.
, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, наз-ся знакопеременным.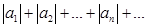 сх-ся, то ряд
сх-ся, то ряд  наз абсолютно сходящимся.
наз абсолютно сходящимся.
 - ряд из абсол значений величин.Доказана сх-ть по 2-му признаку сравнения, след-но исх ряд сх-ся абсолютно.
- ряд из абсол значений величин.Доказана сх-ть по 2-му признаку сравнения, след-но исх ряд сх-ся абсолютно. (19)
(19)
 (1)
(1)

 сх-ся, то ряд
сх-ся, то ряд  наз абсолютно сходящимся.
наз абсолютно сходящимся.
 - ряд из абсол значений величин
- ряд из абсол значений величин , где
, где  - числа, называемые коэффициентами ряда, x – переменная, наз-ся степенным рядом. Интервал (-R;R) наз интервалом сх-ти степ ряда. Заметим, что для x?(-R;R) ряд сходится абсолютно, а в точках x= ± R степенной ряд может сходиться или расходиться. Для нахождения радиуса сходимости можно воспольз-ся, признаками Даламбера или Коши. Теорема. Если существует
- числа, называемые коэффициентами ряда, x – переменная, наз-ся степенным рядом. Интервал (-R;R) наз интервалом сх-ти степ ряда. Заметим, что для x?(-R;R) ряд сходится абсолютно, а в точках x= ± R степенной ряд может сходиться или расходиться. Для нахождения радиуса сходимости можно воспольз-ся, признаками Даламбера или Коши. Теорема. Если существует  | an+1/ an|=L, то R=1/L=
| an+1/ an|=L, то R=1/L= 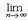 | an/ an+1|. (Док-во. Рассмотрим ряд
| an/ an+1|. (Док-во. Рассмотрим ряд  anxn. Применим к нему признак Даламбера.
anxn. Применим к нему признак Даламбера.  | an+1xn+1/ anxn|=
| an+1xn+1/ anxn|=  | an+1/ an|∙| x | =L∙| x |. Отсюда следует, что если L∙| x |<1, т,е. если | x |<1/L, то ряд сходится абсолютно. Если L∙| x |>1, то ряд расходится. Теорема доказана.) Заметим, что если L=0, для любого | x | то R=∞. Если L=∞, для любого x≠0, то R=0. Если R=0, то ряд сходится в единственной точке x0=0; если R=∞, то ряд сходится на всей числовой прямой. Итак, интервал сходимости ряда
| an+1/ an|∙| x | =L∙| x |. Отсюда следует, что если L∙| x |<1, т,е. если | x |<1/L, то ряд сходится абсолютно. Если L∙| x |>1, то ряд расходится. Теорема доказана.) Заметим, что если L=0, для любого | x | то R=∞. Если L=∞, для любого x≠0, то R=0. Если R=0, то ряд сходится в единственной точке x0=0; если R=∞, то ряд сходится на всей числовой прямой. Итак, интервал сходимости ряда  anxn есть (-R;R). Для нахождения области сходимости ряда надо отдельно исследовать сходимость в точках x=R и x=-R; в зав-ти от рез-тов этого исслед-я обл-ю сх-ти ряда м. б. один из промежутков: [-R;R],(-R;R),[-R;R),(-R;R]. Теорема Абеля: 1) Если степенной ряд
anxn есть (-R;R). Для нахождения области сходимости ряда надо отдельно исследовать сходимость в точках x=R и x=-R; в зав-ти от рез-тов этого исслед-я обл-ю сх-ти ряда м. б. один из промежутков: [-R;R],(-R;R),[-R;R),(-R;R]. Теорема Абеля: 1) Если степенной ряд  anxn сходится при x=x0, то он сходится причем абсолютно для всех x, удовлетворяющих неравенству |x|<|x0|. 2) Если же ряд
anxn сходится при x=x0, то он сходится причем абсолютно для всех x, удовлетворяющих неравенству |x|<|x0|. 2) Если же ряд 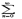 anxn расходится при x=x1, то он расходится при всех x, удовлетворяющих условию |x|>|x1|. (Док-во 1)Так как числовой ряд
anxn расходится при x=x1, то он расходится при всех x, удовлетворяющих условию |x|>|x1|. (Док-во 1)Так как числовой ряд  anx0n сходится, то
anx0n сходится, то 
 anx0n=0. Это означает, что числовая последовательность {anx0n} ограничена.Тогда перепишем степенной ряд в виде a0 + a1x0 (x/x0) + a2x02(x2/x02) +…+…=
anx0n=0. Это означает, что числовая последовательность {anx0n} ограничена.Тогда перепишем степенной ряд в виде a0 + a1x0 (x/x0) + a2x02(x2/x02) +…+…=  anx0n (x/x0)2. Рассмотрим ряд из абсолютных величин. |a0| + |a1x0 (x/x0) | + |a2x02(x2/x02) | +…+…<= M + M| x/x0| + M| x/x0|2 +…= M(1+q+ q2+…). Это геометрическая прогрессия с q=(x/x0)<1—сходится. Из признака сравнения следует абсолютная сходимость степенного ряда. 2)От противного. Пусть степенной ряд сходится при некотором x*, | x*|> x1. Но тогда согласно 1-ой части теоремы, степенной ряд сходится для всех | x |< x*. В том числе должен сходится и при x= x0, так как | x |< | x*|. Но это противоречит предположению теоремы. Теорема доказана.)
anx0n (x/x0)2. Рассмотрим ряд из абсолютных величин. |a0| + |a1x0 (x/x0) | + |a2x02(x2/x02) | +…+…<= M + M| x/x0| + M| x/x0|2 +…= M(1+q+ q2+…). Это геометрическая прогрессия с q=(x/x0)<1—сходится. Из признака сравнения следует абсолютная сходимость степенного ряда. 2)От противного. Пусть степенной ряд сходится при некотором x*, | x*|> x1. Но тогда согласно 1-ой части теоремы, степенной ряд сходится для всех | x |< x*. В том числе должен сходится и при x= x0, так как | x |< | x*|. Но это противоречит предположению теоремы. Теорема доказана.) с областью сходимости (-R;R). Тогда сумма S(x) явл дифференцируемой функцией в инт (-R;R). Ее произв S'(x)=
с областью сходимости (-R;R). Тогда сумма S(x) явл дифференцируемой функцией в инт (-R;R). Ее произв S'(x)= 
 (-R;R).
(-R;R).



