
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритмічна та програмна реалізація методу Рунге-Кутта четвертого порядку
Var x0,y0,x,y,b,h: real; k1,k2,k3,k4: real; i,n: integer; … Begin <введення вихідних даних> h:=(b-x0)/n; x:=x0; y:=y0; for i:=1 to n do begin k1:=x+y; k2:=(x+h/2)+(y+h*k1/2); k3:=(x+h/2)+(y+h*k2/2); k4:=(x+h)+(y+h*k3); у:=у+h*(k1+2*k2+2*k3+k4)/6; <виведення x,y> x:=x+h; end; end.
Примітка: у програмі реалізовано розв’язання диференційного рівняння, що розглянуте у прикладі.
Порядок виконання роботи Вибрати індивідуальне завдання у Таблиці 10.1. і виконати всі пункти завдання із Розділу 10.3, застосувавши для розв’язання заданого диференційного рівняння метод Рунге-Кутта четвертого порядку. Заняття № 12 Розробка програми визначення екстремумів функцій градієнтним методом Мета роботи: Закріплення знань із застосування градієнтних методів для визначення екстремумів функцій, розробка відповідного алгоритму і програми на мові Pascal і застосування її для розв’язання індивідуального завдання. Теоретичні відомості Загальні положення Екстремумом функції На параметри На траєкторії спуску кожна наступна точка
Координати кожної точки на траєкторії спуску обчислюються за рекурентною формулою:
де
Градієнтний метод Градієнтом функції Протилежний йому напрям антиградієнта Визначений таким чином напрям вектора-градієнта (антіградієнта) дозволяє виконувати оптимальні кроки і спрямовувати траєкторію спуску в бік екстремума функції, який треба знайти. Саме тому в градієнтному методі кроки оптимізації виконуються вздовж вектора градієнта:
Знак залежить від виду екстремуму функції, який визначається: знак “+” - при пошуку максимуму функції, знак “-” – мінімуму. Вектор-градієнт
Вони є складовими вектора, визначають його напрям і довжину. Для визначення чергового кроку З врахуванням (12.1) і (12.2) рекурентна формула градієнтного метода набуває вигляду:
Вона дозволяє отримати координати чергової При наближенні до екстремуму функції довжина вектора-градієта зменшується. В точці екстремуму вона дорівнює нулю. Якщо чергова точка траєкторії
де Координати цієї точки Загальний алгоритм визначення екстремума функції градієнтним методом 1. Підготовчий етап: · визначення структури вектора-градієнта і аналітичних виразів його складових 2. вибір коефіцієнту кроку 3. Вибір і завдання начальних наближень вектора змінних 4. Обчислення значень похідних функції (складових вектора-градієнта) в точці
5. Контроль завершення відповідно до умов (12.5). Якщо ці умови не виконуються – перехід до п. 5, якщо виконується – до п. 6; 6. Виконання кроку вздовж вектора-градієнта, заданого його складовими, відповідно до (12.4), визначення координат чергової точки
Повернення до п. 3; 7. Точка траєкторії спуску Обчислюємо значення функції в цій точці
Приклад визначення екстремумів функції градієнтним методом Знайти максимум функції однієї змінної
1. Визначаємо структуру вектора-градієнта. Він має одну складову:
Приймаємо коефіцієнт кроку 2. Як початкове наближення параметра беремо початок інтервалу
Виконуємо крок оптимізації ( 3. Вектор-градієнт в точці початкового наближення х(0):
4. Контроль завершення відповідно до (12.5):
Необхідно виконати наступний крок (к=1). 5. Координати наступної точки траєкторії спуску відповідно до (12.4):
Значення функції в цій точці: F(X(1)) = 0.1*(Х(1))3 – 2*(Х(1))2 + 10*Х = 0.1*(2.6875)3 – 2*(2.6875)2 +10*2.6875 =14.3708. Переходимо до наступного кроку (
Повторюємо кроки оптимізації до досягнення заданої точності. Результати розрахунків записуємо в таблицю:
Після виконання 23-го кроку оптимізації довжина вектора-градієнта становить:
Розрахунок закінчується. Максимум функції з точністю На хід процесу оптимізації можно впливати, змінюючи коефіцієнт кроку
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 122; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.77.71 (0.019 с.) |

 називається її мінімальне або максимальне значення. У загальному випадку функція може мати декілька екстремумів. Один із них – головний - називається глобальним, інші - локальні. Задача пошуку екстремумів зводиться до їх локалізації і уточнення значень параметрів
називається її мінімальне або максимальне значення. У загальному випадку функція може мати декілька екстремумів. Один із них – головний - називається глобальним, інші - локальні. Задача пошуку екстремумів зводиться до їх локалізації і уточнення значень параметрів 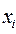 та функції
та функції 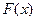 в точці екстремума.
в точці екстремума.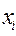 накладаються, зазвичай, обмеження у вигляді нерівностей
накладаються, зазвичай, обмеження у вигляді нерівностей 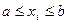 . В межах відрізку
. В межах відрізку  функцію вважаємо унімодальною, тобто такою, що має один екстремум. За таких умов для пошуку екстремуму функції найчастіше застосовують методи можливих напрямків. Це методи послідовних наближень, у яких, в результаті виконання ряду кроків оптимізації
функцію вважаємо унімодальною, тобто такою, що має один екстремум. За таких умов для пошуку екстремуму функції найчастіше застосовують методи можливих напрямків. Це методи послідовних наближень, у яких, в результаті виконання ряду кроків оптимізації  у просторі параметрів, формується послідовність точок
у просторі параметрів, формується послідовність точок 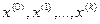 , що збігається до точки екстремума функції
, що збігається до точки екстремума функції  . Їх сукупність складає траєкторію спуску до мінімуму (максимуму) функції.
. Їх сукупність складає траєкторію спуску до мінімуму (максимуму) функції. повинна бути кращою за попередню точку
повинна бути кращою за попередню точку  по критерію оптимальності:
по критерію оптимальності: - якщо визначається мінімум функції
- якщо визначається мінімум функції  - якщо визначається максимум функції.
- якщо визначається максимум функції. (12.1)
(12.1) - вектори координат
- вектори координат  -ї і наступної
-ї і наступної 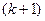 -ї точок траєкторії;
-ї точок траєкторії;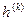 - коефіцієнт кроку. Дозволяє впливати на довжину кроку при переході від точки
- коефіцієнт кроку. Дозволяє впливати на довжину кроку при переході від точки  ;
; - крок, задає напрям кроку.
- крок, задає напрям кроку.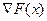 .
. показує шлях найшвидшого зменшення функції.
показує шлях найшвидшого зменшення функції. (12.2)
(12.2)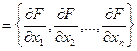
 (12.3)
(12.3)  необхідно обчислювати, відповідно до (12.2), значення похідних
необхідно обчислювати, відповідно до (12.2), значення похідних  .
.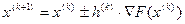 (12.4)
(12.4)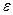 , то виконуватиметься умова:
, то виконуватиметься умова: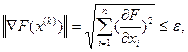 (12.5)
(12.5)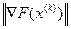 -
-  .
. і значення функції в ній
і значення функції в ній  і є розв’язком задачі.
і є розв’язком задачі.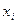 ;
; ;
; , які є координатами початкової точки траєкторії спуску. Обчислення значення функції в цій точці
, які є координатами початкової точки траєкторії спуску. Обчислення значення функції в цій точці  ;
;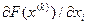 ;
;
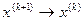 .
.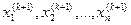 визначені в результаті останнього кроку, є шуканим екстремумом функції із заданою точністю
визначені в результаті останнього кроку, є шуканим екстремумом функції із заданою точністю 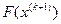 .
. в інтервалі
в інтервалі 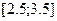 з точністю
з точністю 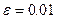 .
.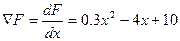 .
.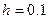 ;
;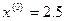 . Значення функції в цій точці:
. Значення функції в цій точці:
 ).
).
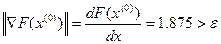 .
.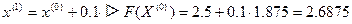 .
.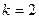 ):
):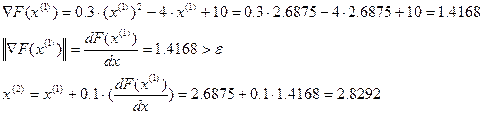

 .
. і досягається при
і досягається при 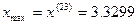 після виконання 23-х кроків оптимізації в напрямку вектора-градієнта. При цьому монотонно зменшується довжина вектора
після виконання 23-х кроків оптимізації в напрямку вектора-градієнта. При цьому монотонно зменшується довжина вектора 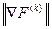 (збігається до нуля) і збільшується значення функції
(збігається до нуля) і збільшується значення функції 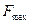 .
.


