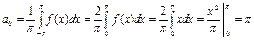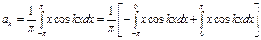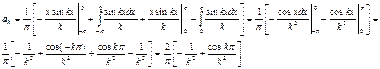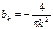Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложение взаимноперпендикулярных колебаний.
В результате сложения взаимноперпендикулярных колебаний получаются сложные в общем случае по виду траектории движения. Поэтому мы рассмотрим частный случай, когда складываемые колебания имеют одинаковые частоты, но разные амплитуды и фазы. В этом случае отдельные составляющие можно записать в виде Для определения вида траектории результирующего движения из закона движения следует исключить время.
Даже в этом простом случае уравнение траектории для произвольного сдвига фаз между отдельными колебаниями принимает сложный вид. Мы рассмотрим частные случаи сдвига фаз. а) Упрощая выражение, получаем, что б) .Отсюда следует, что в) ,т.е. представляет собой эллипс. Следует заметить, что как при сдвиге фаз представляют собой только частный случай так называемых фигур Лиссажу. Фигурами Лиссажу называют траектории, описываемые точкой, совершающей одновременно два гармонических колебания во взаимноперпендикулярных направлениях. Таким образом, по виду фигуры Лиссажу можно определить соотношение между частотами и фазами складываемых колебаний, а также оценивать, насколько сильно они отличаются от гармонических.
В конце прошлого века Фурье доказал, что справедливо и противоположное утверждение: любое периодическое движение можно представить в виде суммы гармонических составляющих. Математически это представление называется рядом Фурье. Согласно Фурье, любой периодический процесс
При анализе периодических движений оба представления Фурье эквивалентны. На амплитуды отдельных гармонических составляющих накладываются определённые ограничения, и они вычисляются по приведенным ниже соотношениям:
где Постоянная При вычислении коэффициентов Фурье
а если функция
Пользуясь этими общими правилами вычисления коэффициентов Фурье, рассмотрим разложение в тригонометрический ряд нескольких частных типов периодических колебаний, часто встречающихся в практике физических измерений и работе различных приборов. а) Колебания прямоугольной формы. Колебания прямоугольной формы (рис. 110) могут быть представлены функцией
 , является периодической. , является периодической.
Так как исследуемая функция является нечётной, то 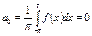
Как видно, коэффициенты
а для четных
Учитывая полученные значения коэффициентов разложения в ряд Фурье (348), (349), и (350), можно окончательно записать ряд Фурье для колебаний прямоугольной формы в виде
б) Колебания пилообразной формы
Периодические колебания пилообразной формы, представленные на рис. 111, можно описать функцией 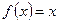 , определяемой в промежутке , определяемой в промежутке  . При других значениях аргумента . При других значениях аргумента  функция повторяется с периодом функция повторяется с периодом  . .
Как видно, Полагая
Таким образом, коэффициенты Фурье
а при нечётных
в) Колебания треугольной формы Колебания треугольной формы (рис.112) описываются функцией
В этом выражении значения интегралов находим по правилу интегрирования по частям, как в предыдущем случае:
Для чётных значений
а для нечётных
Используя найденные значения коэффициентов
Упругие волны. Для распространения колебаний, возбуждаемых источником, необходимо наличие упругой среды.
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 174; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.174.168 (0.016 с.) |
 и
и 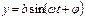 . Здесь
. Здесь  - сдвиг фаз между складываемыми колебаниями.
- сдвиг фаз между складываемыми колебаниями.

 . При таком сдвиге фаз уравнение траектории принимает вид
. При таком сдвиге фаз уравнение траектории принимает вид 
 т.е. траектория представляет собой прямую линию, которая лежит в первом и третьем квадрантах.
т.е. траектория представляет собой прямую линию, которая лежит в первом и третьем квадрантах. . При таком сдвиге фаз уравнение траектории преобразуется к виду
. При таком сдвиге фаз уравнение траектории преобразуется к виду 
 , т.е. и в этом случае траектория представляет собой прямую линию с тем же наклоном, но она лежит уже во втором и четвёртом квадрантах.
, т.е. и в этом случае траектория представляет собой прямую линию с тем же наклоном, но она лежит уже во втором и четвёртом квадрантах.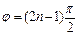 . Уравнение траектории для такого сдвига фаз имеет вид
. Уравнение траектории для такого сдвига фаз имеет вид 
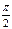 , так и при
, так и при  уравнение траектории имеет один и тот же вид.
уравнение траектории имеет один и тот же вид.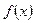 , протекающий с частотой
, протекающий с частотой  может быть представлен бесконечным тригонометрическим рядом
может быть представлен бесконечным тригонометрическим рядом или
или 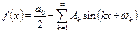
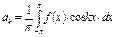 и
и 
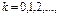 а пределы интегрирования определяются тем промежутком, в котором определена сама изучаемая функция
а пределы интегрирования определяются тем промежутком, в котором определена сама изучаемая функция 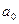 разложения в ряд Фурье определяется из соотношения:
разложения в ряд Фурье определяется из соотношения: 
 и
и  часто бывает полезно пользоваться тем, что если функция
часто бывает полезно пользоваться тем, что если функция  четная в промежутке
четная в промежутке  , т.е.
, т.е. 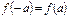 , то
, то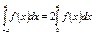
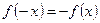 , то
, то
 , в промежутке
, в промежутке 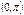 и
и  в промежутке
в промежутке  , т.е. функция
, т.е. функция  в данном
в данном




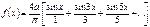
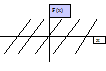



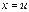 и
и 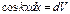 , находим далее, что
, находим далее, что  , а
, а 

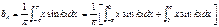
 .
.  .
.
 при чётных значениях равны
при чётных значениях равны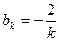
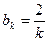

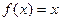 , определённой в промежутке
, определённой в промежутке 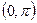 и
и 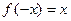 , определённой в промежутке
, определённой в промежутке 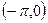 . Так как
. Так как  , функция является чётной, а для чётной функции по
, функция является чётной, а для чётной функции по