
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типичные ошибки в решениях задачи 15Стр 1 из 8Следующая ⇒
Задача 15 В профильном ЕГЭ 2015 года модель задачи 15 (ранее – задача С1) не претерпела никаких изменений по сравнению с прошлым годом. Уже традиционно, это была задача, состоящая из двух пунктов: решить тригонометрическое уравнение и отобрать корни уравнения из указанного промежутка. Задача 15 предполагала: – знание основных тригонометрических формул (основное тригонометрическое тождество); – владение методом замены переменной при решении уравнения; – умение решать квадратные уравнения; – вычислительные навыки работы с числовыми иррациональными выражениями; – умение решать простейшие тригонометрические уравнения по общим и частным формулам; – знание области значений тригонометрических функций; – владение хотя бы одним из способов отбора корней тригонометрического уравнения из указанного промежутка: с помощью единичной окружности, решением двойного неравенства, перебором, с помощью графика функции. Приведем один из примеров задачи 15: а) Решите уравнение: б) Укажите корни этого уравнения, принадлежащие отрезку Типичные ошибки в решениях задачи 15 Одной из самых распространенных ошибок при решении задачи 15 в 2015 году были неточности и заблуждения в формулах корней простейших тригонометрических уравнений: использование формулы корней для простейшего тригонометрического уравнения относительно синуса – к уравнению относительно косинуса и наоборот, неверная периодичность корней, описки и другие ошибки в записи корня. Эти ошибки приводили к тому, что решения уравнения указывались неверно, и как следствие – первый пункт задачи не был выполнен. Пример 1.
Рис. 10.1. Комментарий: Ошибка учащегося на Рис. 10.1. заключается в незнании формул корней простейшего тригонометрического уравнения. В частности (при нахождении первой серии решений), использование формулы корней простейшего тригонометрического уравнения относительно косинуса как формулы корней уравнения относительно синуса. Эта ошибка была очень распространена среди работ участников экзамена 2015 года. Решение пункта а) содержит еще одну грубую ошибку (о которой будет сказано позднее) – невладение областью значений тригонометрических функций (
Пример 2.
Рис. 10.2. Комментарий: Единственной ошибкой в решении пункта а) на рисунке 10.2. является ошибка в записи корня уравнения: 2. Не менее редкой ошибкой при решении задачи 15 в 2015 году было неверное вычисление значения обратной тригонометрической функции: либо неверные значения аркфункций, либо неверное преобразование аркфункций отрицательного аргумента. Эти ошибки также приводили к тому, что корни уравнения указывались неверно, и как следствие – первый пункт задачи не был выполнен. Пример 3.
Рис. 10.3. Комментарий: При решении простейшего тригонометрического уравнения Пример 4.
Рис.10.4. Комментарии: В решении, приведенном на рисунке 10.4., досадная ситуация: одно лишь неверное преобразование арккосинуса отрицательного аргумента свело весь результат к 0 баллов. Учащийся, видимо, считает, что 3.Достаточно много ошибок было связано с незнанием множества значений тригонометрических функций синус и косинус. Учащиеся записывали формулу корней тригонометрических уравнений
Пример 5.
Рис.10.5. Комментарии: В работе на рисунке 10.5. учащийся в решение записывает несуществующее значение 4. К типичным ошибкам при решении задачи 15 можно отнести потерю корней при переходе от решения простейшего тригонометрического уравнения в общем виде к частному виду. Пример 6.
Рис. 10.6. Комментарий: Записав верное решение уравнения Рис. 10.7. Комментарий: Среди работ 2015 года ошибка такого рода приобрела популярность. Учащийся сводит глобальное решение уравнения к исследованию одного частного случая. В данном случае, рассматривая равенство суммы нулю только в том случае, когда каждое слагаемое равно нулю. При чем, эти размышления проводятся без логических связок «и» или «или», но по решению очевидно, учащийся имеет в виду связку «или», что делает рассуждение еще более неправильным. Оценка – 0 баллов. Рис. 10.8. Комментарий: На рисунке 10.8. приведено решение, содержащее изначально ошибку при раскрытии скобок в момент использования основного тригонометрического тождества, что возможно было бы приравнять к описке или вычислительной ошибке. Но, кроме этого, оба простейших тригонометрических уравнения не имеют решения в силу множества значений синуса, на что учащийся не обращает внимания и приводит неверные решения уравнения. Оценка – 0 баллов. 7. Нехарактерная в прошлых годах для задачи такого типа ошибка – неумение работать с иррациональными числовыми выражениями. В связи с этим, для многих учащихся решение квадратного уравнения с иррациональными коэффициентами представляло трудность (чаще всего решение не доводилось до конца). Пример 9.
Рис.10.9. Комментарий: В решении на рисунке 10.9. нет ошибок. Но решение не доведено до конца. Упростив полученные иррациональные выражения, учащийся смог бы сделать вывод о решениях уравнения. Оценка – 0 баллов. 8. По-прежнему, как и в прошлых годах, учащиеся теряют баллы в пункте б) решения задачи 15 по причине отсутствия обоснования отбора корней из промежутка. 1 балл за решение пункта б) выставляется при условии присутствия «следов» отбора корней, что зачастую не имело места в работах участников экзамена 2015 года. Пример 10.
Рис.10.10. Комментарий: В решении на рисунке 10.10. приведено верное, достаточно обоснованное решение пункта а). Но «следы» отбора корней из указанного промежутка отсутствуют (хотя в ответе указаны правильно отобранные корни для пункта б)), что дает эксперту право выставить только 1 балл.
Следует отметить, что по сравнению с 2014 годом при решении задачи 15 улучшилась ситуация с обоснованным отбором корней их промежутка. Учащиеся активно использовали различные способы отбора корней: перебор, решая двойное неравенство, используя единичную окружность или график функции. В основном это было успешно.
Задача 16 В 2015 году задача 16 (ранее задача С2) без изменения тематики (Прямые и плоскости в пространстве. Многогранники. Тела и поверхности вращения. Измерение геометрических величин. Координаты и векторы.) стала содержать два пункта с требованиями «доказать» и «найти». Каждый из пунктов независимо оценивался 1 баллом. Задача 16 предполагала: – владение как стереометрическими понятиями (такими как пирамида, высота пирамиды, перпендикулярность прямой и плоскости, угол между прямой и плоскостью и др.) так и планиметрическими (в частности, понятием прямоугольного треугольника, определениями тригонометрических функций острого угла прямоугольного треугольника и др.), а также фактами, связанными с этими понятиями; – умение изображать пирамиду, проводить дополнительные построения, направленные на изображение и поиск угла между прямой и плоскостью; – знание признаков перпендикулярности прямой и плоскости и умение их использовать при решении задачи; – знание обратной теоремы Пифагора и умение ею воспользоваться в нужной ситуации; – владение навыками нахождения угла по значению тригонометрической функции при выполнении вычислительной составляющей решения. Приведем один из примеров задачи 16: В основании четырехугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB = 3 и BC = 4. Длины боковых ребер пирамиды а) Докажите, что SA – высота пирамиды. б) Найдите угол между прямой SC и плоскостью ASB. Рис. 11.1. Комментарии: В решении пункта а) задачи 16 на рисунке 11.1. содержится типовая ошибка, заключающаяся в незнании (или неверном понимании) признака перпендикулярности прямой и плоскости. Рассмотрение одного треугольника и доказательство его прямоугольности с помощью обратной теоремы Пифагора, дает основание утверждать только перпендикулярность прямой SA и AD, чего недостаточно для заключения перпендикулярности прямой SA и плоскости ABCD. Решение пункта б) отсутствует. Оценка в таком случае – 0 баллов. 2. Неверное определение искомого угла между прямой и плоскостью (неверный переход к планиметрической задаче) стало также одно из наиболее распространенных типовых ошибок при выполнении пункта б) задачи 16. Процедура определения угла между прямой и плоскостью требует особых рассуждений и дополнительных построений (проекции прямой на плоскость). Однако, многими учащимися искомый угол между прямой и плоскостью был определен интуитивно, без необходимых умозаключений, что, чаще всего, было ошибочным и сводило все решение пункта б) к 0 баллов.
Пример 2.
Рис.11.2. Комментарии: Решение пункта б) задачи 16 на рисунке 11.2. оценено 0 баллов, т.к. искомый угол между прямой SC и плоскостью ASB определен неверно. Учащимся даже предпринята попытка построения искомого угла по всем правилам – проведен перпендикуляр (видимо, с целью построения проекции прямой на плоскость), но, к сожалению, не из точки С, а из точки А. Это говорит о том, что у учащегося есть некоторое общее представление об угле между прямой и плоскостью, но недостаточно полное. Часто в решениях пункта б) отсутствовали необходимые дополнительные построения искомого угла, а сам угол просто констатировался (неверно) учащимся без каких-либо пояснений. Все эти случаи сводились к 0 баллов. 3. Распространенным недостатком в решении задачи 16 было отсутствие теоретических ссылок и обоснований логических переходов. Учащиеся не указывают используемую для вывода теорию: определения, теоремы, признаки, свойства и т.д.
Рис.11.3. Комментарии: В доказательстве учащимся приводятся некоторые обоснования выводов, в частности, ссылка на теорему о трех перпендикулярах, но основания для этого не приведены. Кроме того, в доказательстве обоснована перпендикулярность рассматриваемой прямой и только одной прямой плоскости, чего недостаточно использования признака перпендикулярности прямой и плоскости. Оба пункта не выполнены, оценка – 0 баллов.
Следует отметить, что по сравнению с 2015 годом при решении задачи 16 улучшилась ситуация с указанием верного ответа. В 2014 году одной из распространенных ошибок было в ответ на требование «Найдите угол между…» выписывание значения одной и тригонометрических функций, используемых в решении, что вело к потере баллов, т.к. решение признавалось незавершенным. В 2015 году таких ошибок практически не было. Еще одним достоинством решений задачи 16 в 2015 году было активное использование учащимися нестандартных (для школьного курса геометрии) способов решения (в том числе, координатный, координатно-векторный способы). Также можно констатировать увеличение количества работ с оригинальным решением задачи 16. Приведем примеры некоторых из них.
Рис. 11.4. Комментарии: В решении на рисунке 11.4. угол найден с помощью координатного метода. Грамотно введен вектор
Рис.11.5. Комментарии: Решение на рисунке 11.5. достаточно грамотное. Для нахождения уравнения плоскости по трем точкам учащийся демонстрирует умение работать с определителем, несвойственное школьному курсу математики. Хотя ответ не преобразован, не приведен к эталонному 450, он является правильным. Оценка – 2 балла.
Рис. 11.6. Комментарии: К оригинальным решениям можно отнести доказательство перпендикулярности прямой и плоскости с помощью теоремы косинусов, представленное на рисунке 11.6. Угол между прямой и плоскостью найден также нестандартным для школьного курса математики методом координат. Все рассуждения достаточно обоснованные и верные. Оценка – 2 балла. Задача 17 В профильном ЕГЭ 2015 года модель задачи 17 (ранее – задача С3) претерпела изменения по сравнению с прошлым годом. Вместо системы неравенств была предложена задача: решить «одиночное» неравенство. Задача 17 предполагала: § умение использовать метод введения вспомогательной переменной для решения неравенств; § умение применять метод интервалов; § владение тождественными преобразованиями рациональных выражений, а также показательных и логарифмических выражений и умения оценить равносильность этих преобразований; § владение понятием области допустимых значений неравенства, системы неравенств, совокупности неравенств, в данном случае связанной со свойствами дробно-рациональной функции; § знание свойств показательной и логарифмической функций; § понимание смысла системы неравенств как логической операции «конъюнкции» и совокупности неравенств как логической операции «дизъюнкция» и др. Приведем один из примеров задачи 17 из варианта 579: «Решите неравенство: Участниками ЕГЭ 2015 года были предложены несколько различных способов решения, в том числе отличные от предложенных разработчиками. Основные: метод интервалов с предварительной заменой и так называемый логический, предполагавший рассмотрение случаев неотрицательности дроби (частного). Ниже на рисунках 12.1 и 12.2 приведены примеры работ учащихся с безошибочными решениями задачи №17 описанными способами. Пример 1.
Пример 2.
Рис. 12.2 Комментарии: Решение, согласно критериям, оценено максимальным баллом, не смотря на нерациональное решение неравенства (2).
Рис. 12.3 Комментарии: Автором этого решения, представленного на рис. 12.3 применено неравносильное преобразование, а именно: умножение неравенства на выражение с переменной, знак которого зависит от значения этой переменной. Согласно критериям, оценка – 0 баллов. Заметим также, что в последнем переходе, видимо, ученик допустил описку, вместо
Пример 4.
Рис. 12.4 Комментарии: Автор этого решения неправомерно применил для неравенства свойство пропорции («крест-накрест»), что проиллюстрировал соответствующим знаком. Имеется также ошибка вычислительного характера в последнем переходе решения. Оценка, согласно критериям, 0 баллов.
2. Также очень распространённой ошибкой надо считать переход от дробно-рационального неравенства к неравенству, связывающему числители («отбрасывание» знаменателя). В следующем примере представлена именно такая ошибка.
Пример 5.
Рис. 12.5. Комментарии: нарушена равносильность в определённый момент решения. Можно предположить, что ученик использовал в общем случае неверное утверждение о том, что «дробь неотрицательна при неотрицательном числителе». Согласно критериям, 0 баллов. Заметим также, что в этой работе наблюдается ещё одна достаточно распространённая ошибка: аналитическое и графическое представления ответа не соответствуют друг другу, описывая различные числовые множества. Если бы эта ошибка была единственной, то, согласно критериям, решение могло претендовать на 1 балл.
3. Ряд учащихся вместо неравенства решали уравнение. Соответствующий пример ниже. Пример 6.
Рис. 12.6. Комментарии: Учащийся решал задачу, отличную от сформулированной в КИМ. Согласно критериям, 0 баллов. 4. Как уже отмечалось выше, учащиеся, приступившие к решению задачи №17 и получившие ненулевой балл за эту задачу, применяли в основном метод интервалов, предварительно введя вспомогательную переменную. С применением метода интервалов и введением вспомогательной переменной связан ряд достаточно распространённых ошибок. Отдельные из них, согласно критериям, могут расцениваться как вычислительные (ошибка при определении знаков на промежутках, неверное расположение чисел на числовой прямой), другие – принципиальные, связанные с пропуском шагов алгоритма или неверным их выполнением, не могут быть оценены ненулевым баллом. Приведём примеры. Пример 7.
Рис.12.7. Комментарии: Ошибка в определении знака на одном из интервалов вполне может быть признана вычислительной. Учащийся довёл решение до конца, продемонстрировав в целом владение методом замены переменных и методом интервалов. Согласно критериям, 1 балл. Пример 8.
Рис. 12.8. Комментарии: Не сделана обратная замена – необходимый шаг алгоритма. На числовой прямой отмечены значения исходной и введённой переменной. Согласно критериям, 0 баллов. Отдельные учащиеся применили так называемый логический способ решения, осуществив на определённом этапе равносильный переход к совокупности двух систем. Пример правильного решения этим способом представлен на рисунке 12.2. С этим способом решения неравенства связаны следующие ошибки. Это рассмотрение только одного случая положительности (отрицательности) дроби, неверное использование логической символики. Приведём примеры. Пример 9.
Рис. 12.9. Комментарии: В решении рассмотрен только один случай неотрицательности дроби. При решении неравенства (2) автор решения делает ещё одну ошибку логического характера, рассматривает только один случай неотрицательности произведения. Согласно критериям, 0 баллов.
Пример 10.
Рис. 12.10. Комментарии: в представленном выше решении автор многократно неверно использует логическую символику. В явном виде логические операции «конъюнкция» и «дизъюнкция» в школьном курсе математики не изучаются, не изучаются также законы формальной логики. В связи с этим, а также в связи с тем, что имеется верная последовательность всех шагов решения, работа оценена ненулевым баллом, однако, этот балл не максимальный. 5. Необходимым условием решения неравенств повышенной трудности является устойчивые умения тождественных преобразований выражений, в данном случае дробно-рациональных, показательных и логарифмических. Ошибки этого типа, к сожалению, являются распространенными. Приведём пример работы с одной из очень распространённых ошибок такого типа. Пример 11.
Рис. 12.11. Комментарии: автор решения дважды ошибся при выполнении умножения числа на степень. Согласно критериям, 0 баллов. Задача 18 В профильном ЕГЭ 2015 года модель задачи 18 (ранее – задача С4) не претерпела никаких изменений по сравнению с прошлым годом. Это планиметрическая задача, состоящая из двух пунктов: пункт на доказательство геометрического факта и пункт на нахождение одного из компонентов рассматриваемой конфигурации. Задача №18 предполагала: · владение понятиями вписанного многоугольника (треугольника. четырёхугольника), вписанного и центрального углов, подобия треугольников; · знание геометрических фактов, в частности, таких как признаки подобия треугольников; расположение центра окружности, описанной около треугольника; условие вписанного в окружность четырёхугольника; теорема Пифагора и др.; · умение проводить доказательство геометрических утверждений. Приведём пример задачи № 18 и пример одного из возможных решений, предложенного участником ЕГЭ 2015 года: «Диагонали а) Докажите, что б) Найдите площадь треугольника Пример 1.
Рис. 13.1. Рис. 13.2. Комментарии: Уже при оформлении краткой записи задачи в рубрике «дано» автор этого решения указывает ошибочное условие, утверждая, что Пример 3.
Комментарий: ошибочный вывод из условия о том, что Неполнота решения – также один распространенных недостатков решений задачи № 18 (С4). В решениях часто присутствовало либо только попытка доказательства геометрического факта, либо только попытка вычисления площади. При неполном решении, учащимися чаще отдавалось предпочтение задаче на доказательство, нежели задаче на вычисление. Пример 4.
Рис. 13.4. Комментарий: Присутствует только попытка доказательства пункта а), причём всё с той же типичной ошибкой-заблуждением. Оценка, согласно критериям оценивания, 0 баллов.
Задача 19 В ЕГЭ 2015 года задача 19 абсолютно новая. Это задание высокого уровня сложности с экономическим содержанием, проверяющее практические навыки применения математики в повседневной жизни, навыки построения и исследования математических моделей. Задача 19 предполагала: – умение работать с процентами, частями, долями; – владение понятием «математическая модель»; – умение строить математическую модель задачи; – умение применять математические методы для решения содержательных задач из различных областей науки и практики; – умение интерпретировать полученный результат, учитывать реальные ограничения; – владение вычислительными навыками. Приведем один из примеров задачи 19: «В июле планируется взять кредит в банке на сумму 3 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы: - каждый январь долг возрастает на 20% по сравнению с концом предыдущего года; - с февраля по июнь каждого года необходимо выплатить часть долга; - в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. Чему будет равна общая сумма выплат после полного погашения кредита, если наименьший годовой платеж составит 0,24 млн. рублей». . Самой распространенной ошибкой при решении задачи 19 в 2015 году было неверное понимание условия задачи. Большая часть учащихся, приступивших к выполнению задачи 19, трактовала условие «в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года» как «в июле каждого года долг должен быть на одну и ту же сумму меньше», т.е. как «платеж был одинаковым». Изменив условие задачи, учащиеся решали другую задачу, что оценивалось 0 баллов. Пример 1.
Рис.14.1. Комментарии: В решении на рисунке 14.1. выплата по кредиту считается учащимся постоянной – 1,56 млн. рублей, что не соответствует условию задачи. Оценка – 0 баллов. Пример 2.
Рис.14.2. Комментарии: Рассуждения учащегося в решении на рисунке 14.2. далеки от реального условия задачи. Оценка – 0 баллов. Следует отметить, что некоторые работы все-таки отличались оригинальным решением задачи 19. Приведем примеры таких работ. Пример 3.
Комментарии: В решении на рисунке 14.3. логически связанные, обоснованные верные рассуждения. Размышления ведутся «с конца задачи». Решение сопровождается правильными вычислениями. Оценка – 3 балла. Пример 4.
Комментарии: Решение на рисунке 14.4. учащийся оформляет в виде таблицы, предоставляющей всю необходимую информацию. Рассуждения и вычисления верные, но недостаточно обоснованные, поэтому оценка – 2 балла.
Задача 20 В профильном ЕГЭ 2015 года модель задачи №20 (ранее – задача С5) принципиально не изменилась. Уже традиционно это задача с параметром. На этот раз – система уравнений, одно из которых содержит параметр. Это задача высокого уровня сложности. Задача №20 предполагала: · Наличие обобщенных знаний о различных типах уравнений, их совокупностях и системах; · Владение на высоком уровне понятиями функционально-графической линии курсов алгебры, алгебры и начал анализа и соответствующими умениями; · Владение понятием параметра, модуля действительного числа, уравнения с параметром, системы уравнений; · Умение использовать графическую интерпретацию аналитических данных задачи; · Понимание смысла уравнения с параметром как множества уравнений или множества однотипных линий (с некоторыми исключениями) в прямоугольной системе координат; · Умение выделять случаи при раскрытии модуля и правильно «раскрывать» модуль; · Умение проводить перебор и анализ всевозможных ситуаций, удовлетворяющих вопросу задачи (в данном случае - ситуаций взаимного расположения графиков уравнений системы); · Умение выделять «особые» значения параметра; · Умение использовать частные особенности задачи для рационализации решения и др. Приведём один из примеров задачи №20: «Найдите все значения параметра
Приведем одно из возможных решений задачи 20, предложенное участником ЕГЭ 2015 года. Пример 1.
Рис. 15.1. Комментарий: Участником ЕГЭ предложен графический способ решения. Верный ответ получен обоснованно с помощью верного рассуждения. Согласно критериям оценивания, 4 балла. Рис.15.2. Комментарий: В решении неверно определены точки смены знака подмодульных выражений. Если считать описанную особенность решения опиской, то раскрываются модули также вопреки определению. Согласно критериям, 0 баллов. Задача 21 В профильном ЕГЭ 2015 года задач 21 (ранее – задача С6) традиционно высокого уровня сложности. На этот раз задача 21 предполагала наличие как обобщенных, так и некоторых частных умений в области математики, а также наличия опыта решения нестандартных задач. Перечислим некоторые из предполагавшихся знаний и умений: - умение строить и исследовать простейшие математические модели; - умение различать логическую структуру утверждений с квантором существования и с квантором общности, знание способов доказательства истинности и ложности утверждений с различными кванторами; знание так называемых кванторных законов и умение переформулировать утверждение с помощью этих законов, сохраняя его смысл; - владение понятием натурального числа; - наличие представления о числовых множествах, отличных от множества натуральных чисел; - знание геометрических фактов, таких как условие существования треугольника, теоремы Пифагора и др.
Приведем один из примеров задачи 21 и вариант её решения, предложенный разработчиками: «Три числа назовём хорошей тройкой, если они могут быть длинами сторон треугольника. Три числа назовём отличной тройкой, если они могут быть длинами сторон прямоугольного треугольник. а) Даны 8 различных натуральных чисел. Может ли оказаться, что среди них не найдётся ни одной хорошей тройки? б) Даны 4 различных натуральных числа. Может ли оказаться, что среди них можно найти три отличных тройки? в) Даны 12 различных чисел (не обязательно натуральных). Какое наибольшее количество отличных троек могло оказаться среди них?». а) Если числа равны 1, 2, 4, 8, 16, 32, 64 и 128, то никакие три из них не образуют хорошую тройку. б) Если одно из чисел является длиной гипотенузы для двух треугольников, то какое-то из оставшихся трёх чисел является длиной катета для этих двух треугольников, а тогда треугольники окажутся равными по гипотенузе и катету. Значит, каждое число может быть длиной гипотенузы не более чем одного треугольника. При этом два самых маленьких числа не могут являться длиной гипотенузы треугольника. Значит, среди четырёх чисел можно найти не более одной отличной тройки. в) Упорядочим числа по возрастанию. Самое большое из них может быть длиной гипотенузы не более чем в четырёх треугольниках (в противном случае одно из оставшихся 11 чисел будет длиной катета в двух треугольниках с данной гипотенузой, а тогда эти треугольники будут равны по гипотенузе и катету). Аналогично, второе по величине число может быть длиной гипотенузы не более чем в пяти треугольниках, третье и четвёртое — в четырёх, пятое и шестое — в трёх, седьмое и восьмое — в двух, девятое и десятое — в одном. Итого, отличных троек может получиться не более 30.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 814; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.162.110 (0.177 с.) |
 .
. .
.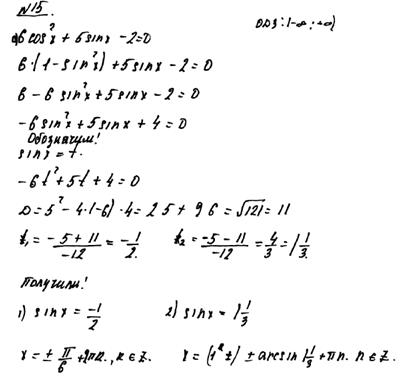

 и
и  ). При этом, выполняя пункт б), автор работы для своих неправильно найденных корней уравнения верно и обоснованно отбирает корни из указанного промежутка. Однако, это не дает основания эксперту поставить 1 балл, т.к. ошибка в пункте а) не может трактоваться как вычислительная (в соответствии с критериями оценивания). Оценка – 0 баллов.
). При этом, выполняя пункт б), автор работы для своих неправильно найденных корней уравнения верно и обоснованно отбирает корни из указанного промежутка. Однако, это не дает основания эксперту поставить 1 балл, т.к. ошибка в пункте а) не может трактоваться как вычислительная (в соответствии с критериями оценивания). Оценка – 0 баллов.
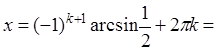
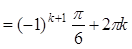 ,
,  вместо верного решения
вместо верного решения 
 ,
,  .
. , учащийся допускает ошибку:
, учащийся допускает ошибку:  считает равным
считает равным  , а не
, а не  . Это делает корни уравнения неверными и приводит к оценке 0 баллов. Кроме этого, решение содержит неуместные условия при замене
. Это делает корни уравнения неверными и приводит к оценке 0 баллов. Кроме этого, решение содержит неуместные условия при замене  ,
, 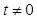 ,
,  ,
,  .
.

 вместо верного
вместо верного  . Возможно перенося свойство четности функции
. Возможно перенося свойство четности функции 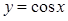 на функцию
на функцию  . При этом, обоснованное и безупречное выполнение пункта б) задачи (для найденного неверного решения) не приносит учащемуся 1 балл, т.к. ошибка, о которой идет речь, не является вычислительной.
. При этом, обоснованное и безупречное выполнение пункта б) задачи (для найденного неверного решения) не приносит учащемуся 1 балл, т.к. ошибка, о которой идет речь, не является вычислительной. или
или  не принимая во внимание условие
не принимая во внимание условие  , при котором эти уравнения вообще имеют решения.
, при котором эти уравнения вообще имеют решения.

 , не отмечая, что
, не отмечая, что 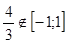 . При отборе корней из промежутка посторонняя серия решений не рассматривается. Для правильного решения обосновано и верно выбраны корни из промежутка. Однако, все это не позволяет эксперту выставить 1 балл, т.к. ошибка в пункте а) не является вычислительной.
. При отборе корней из промежутка посторонняя серия решений не рассматривается. Для правильного решения обосновано и верно выбраны корни из промежутка. Однако, все это не позволяет эксперту выставить 1 балл, т.к. ошибка в пункте а) не является вычислительной.
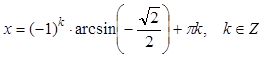 , упрощая выражение в правой части равенства, учащийся допускает ошибку и записывает
, упрощая выражение в правой части равенства, учащийся допускает ошибку и записывает 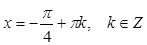 . Последняя формула задает совсем не те значения, которые задает первая формула. В ответ пункта а) записано неверное решение. В пункте б) для неправильной серии решений правильно найдены корни из промежутка, но ошибка в пункте а) не вычислительная, поэтому оценка – 0 баллов.
. Последняя формула задает совсем не те значения, которые задает первая формула. В ответ пункта а) записано неверное решение. В пункте б) для неправильной серии решений правильно найдены корни из промежутка, но ошибка в пункте а) не вычислительная, поэтому оценка – 0 баллов.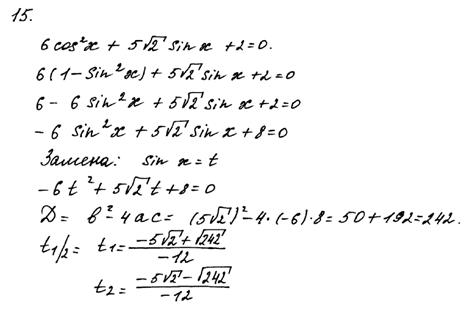
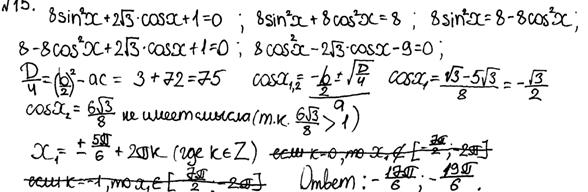
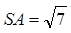 ,
, 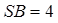 и
и 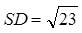 .
.


 . Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б). Оценка – 2 балла.
. Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б). Оценка – 2 балла.




 ».
». Рис. 12.1
Рис. 12.1

 записав
записав 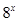 . Учитывая эту погрешность, можно констатировать, что автор этого решения не знает также, что неравенство
. Учитывая эту погрешность, можно констатировать, что автор этого решения не знает также, что неравенство 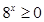 верно при всех значениях переменной. Заметим, что последнее замечание, к сожалению, не редко встречалось и в других работах.
верно при всех значениях переменной. Заметим, что последнее замечание, к сожалению, не редко встречалось и в других работах.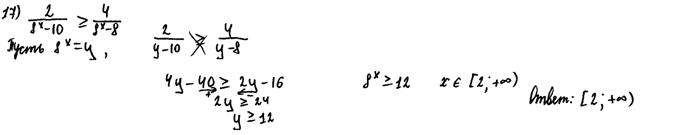
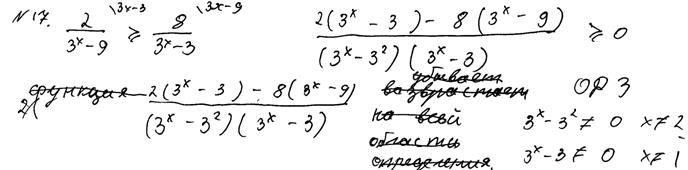
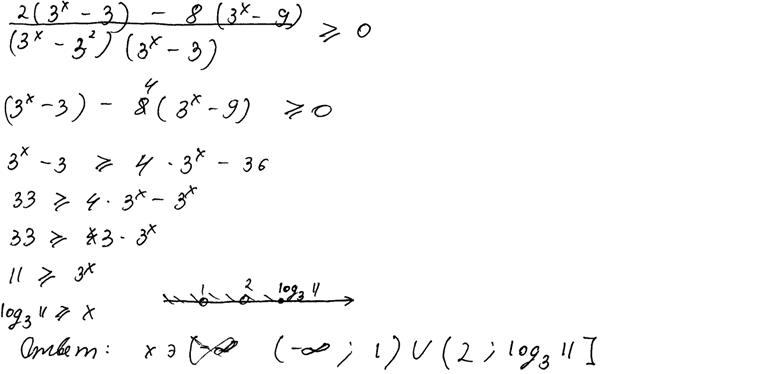
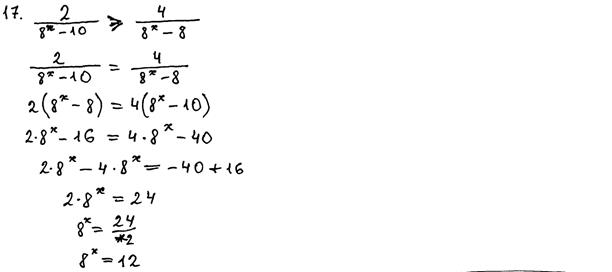

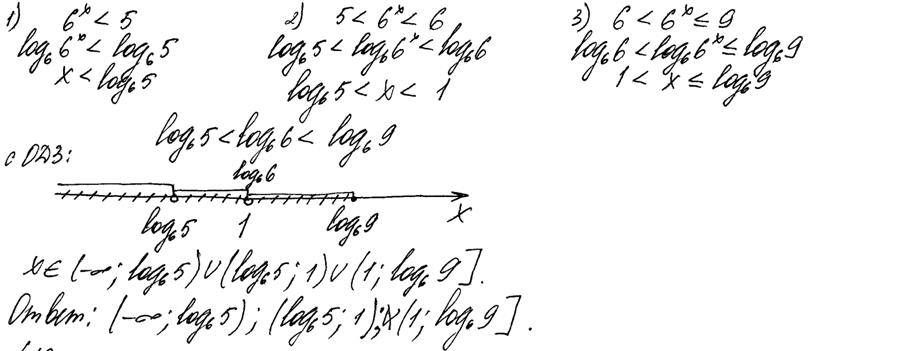
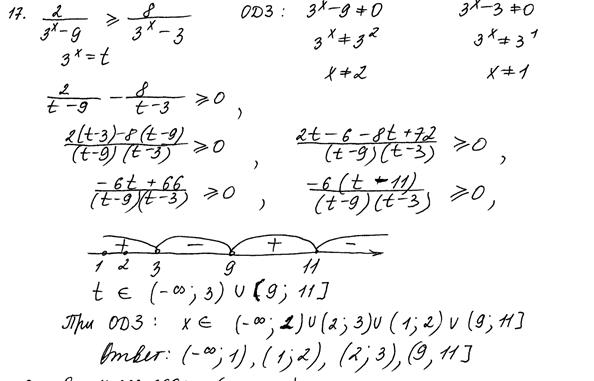
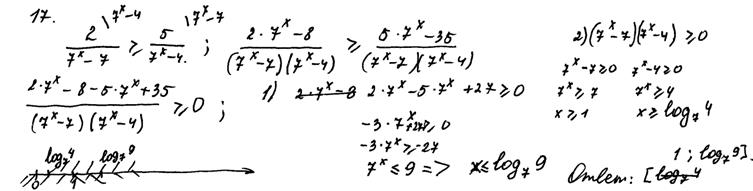

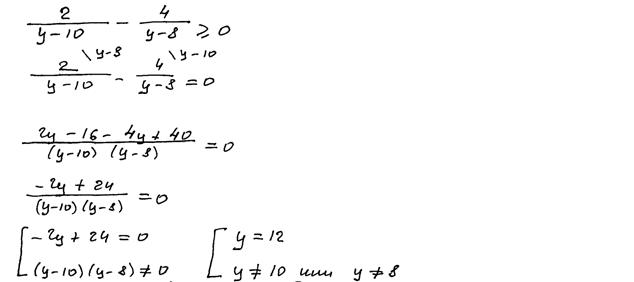
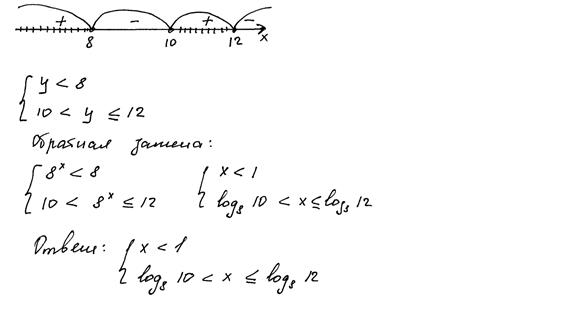

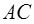 и
и 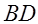 четырёхугольника
четырёхугольника  , вписанного в окружность, пересекаются в точке
, вписанного в окружность, пересекаются в точке  , причём
, причём 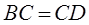 .
.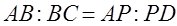 .
. , где
, где  - центр окружности, вписанной в треугольник
- центр окружности, вписанной в треугольник  , если дополнительно известно, что
, если дополнительно известно, что  ».
».
 - вписанный квадрат. Этот факт использован в данном решении как основной. Все остальные ошибки этого решения – следствия необоснованного допущения. Фактически рассматривается задача, отличная от сформулированной в КИМ, или частный случай этой задачи. Согласно критериям, оценка 0 баллов.
- вписанный квадрат. Этот факт использован в данном решении как основной. Все остальные ошибки этого решения – следствия необоснованного допущения. Фактически рассматривается задача, отличная от сформулированной в КИМ, или частный случай этой задачи. Согласно критериям, оценка 0 баллов.
 - ромб. Налицо незнание определения ромба. Кроме того решение содержит противоречащие друг другу записи. Согласно критериям, оценка 0 баллов.
- ромб. Налицо незнание определения ромба. Кроме того решение содержит противоречащие друг другу записи. Согласно критериям, оценка 0 баллов.



 Рис.14.3.
Рис.14.3.
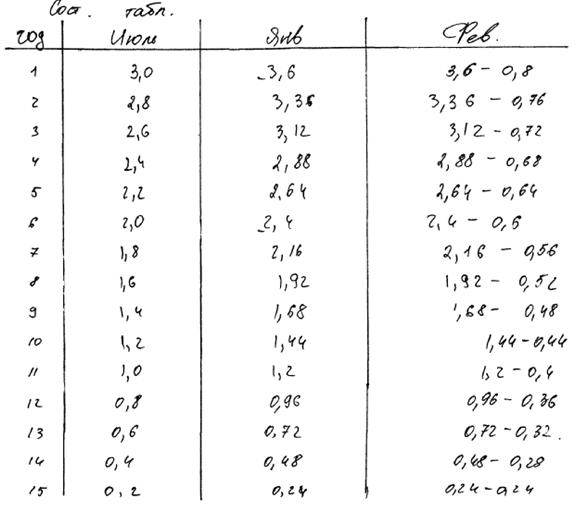
 Рис.14.4.
Рис.14.4. , при каждом из которых система уравнений
, при каждом из которых система уравнений  имеет более двух решений».
имеет более двух решений».




