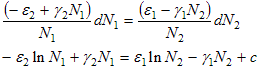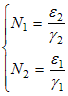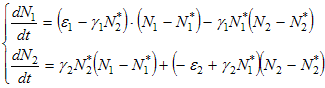База данных Access. Поиск данных при помощи запросов. Логические операции, используемые в запросах

Математические модели системы из двух взаимодействующих популяций.

Математические модели системы из двух взаимодействующих популяций

 

Рассмотрим сообщество, состоящее из двух видов, один из которых - хищник, другой - жертва.
N₁(t) - численность жертвы.
N₂(t) - численность хищника.

Сформулируем основные положения модели:
1. Два вида (хищник и жертва) существуют изолированно на ограниченной территории (другие виды не оказывают влияния на их численность).
2. В отсутствие хищника жертва развивается по мальтусовскому закону роста. ε₁ - коэффициент прироста жертвы в отсутствие хищника; ε₁ = const > 0.
3. Хищник питается только жертвой. В отсутствие жертва он развивается по экспоненциальному закону гибели, при этом коэффициент прироста хищник -ε₂, где ε₂ = const >0 - коэффициент смертности.
4. Поедание жертвы хищником пропорционально численности жертвы (один хищник поедает в единицу времени количество жертв, пропорциональное численности жертв, а общее количество жертв, поедаемых в единицу времени будет пропорционально произведению численности жертв и численности хищников). γ₁N₁N₂ определяет, на какую величину изменяется количество жертв в единицу времени. γ₁ = const >0 - коэффициент истребления.
5. Прирост биомассы хищников пропорционален количеству съеденной биомассы жертв. И тогда в единицу времени количество хищников увеличивается на γ₂N₁N₂, γ₂ = const > 0 - коэффициент переработки съеденной биомассы.
(ε₁ - γ₁N₂) - коэффициент прироста жертвы в расчете на одну особь.
(-ε₂ + γ₂N₁) - коэффициент прироста хищника в расчете на одну особь.

Составим уравнение, описывающее динамику численности:

(1)

- классическая модель "хищник-жертва" (модель Лотка-Вольтерра).

(2)

- начальные условия.
Получили задачу Коши.

Исследуем модель. Выясним характер поведения функций N₁, N₂ и установим траектории развития сообщества. Исключим параметры, поделив первое уравнение системы на второе.

Разделяем переменные и интегрируем правую и левую часть. Ищем ненулевые решения.

Запишем решение в виде первого интеграла:

(3)

c находится, исходя из заданных ненулевых условий.
(3) - уравнение фазовых траекторий за исключением особых точек (когда правые части приравниваются к нулю). Уравнение (3) определяет замкнутые линии с центром в точке с координатами (ε₂/γ₂; ε₁/γ₁).

Положения равновесия

Найдем все положения равновесия системы. Приравниваем правую часть к нулю, ищем решения системы:

Система имеет два различных решения:
1. P₀(0, 0), N₁ = N₂ = 0. Если N₁ = 0, то N₂ = 0 и наоборот.
2. Ненулевое положение равновесия - P₁:

Получаем, что в классической модели две точки покоя.

Характер устойчивости

Для анализа на устойчивость используем линеаризацию. Пусть P^* = (N₁^*, N₂^*) - произвольная точка покоя. Разложим функции правой части в ряд Тейлора, сохраняя только линейные слагаемые. Учитывая, что f(N₁^*, N₂^*) = 0, получаем:

Обозначим

Тогда система примет вид:

(4)

Нулевое положение равновесия линеаризованной системы (4) будет соответствовать исходному положению равновесия P^* системы (1). Устойчивость системы (4) зависит от вещественной части собственных значений матрицы системы.
Исследуем каждое положение равновесия.
Первая точка покоя. P^* = P₀(0, 0). Система примет вид:

λ₁ = ε₁, λ₂ = -ε₂. Оба собственных значения - вещественные, разного знака, значит, положение равновесия P₀ - седло. Найдем уравнения сепаратрис седла в виде y = kx:

Построим фазовый портрет системы.

Сепаратрисами седла являются координатные оси. Для оси x отклонения нарастают, для y - затухают с течением времени. Таким образом, можно определить направление движения по траекториям.
Вторая точка покоя. P^* = P₁.

Матрица системы:

Характеристическое уравнение:

Собственные числа мнимые с нулевой вещественной частью. P₁ устойчиво, но не асимптотически. Точка покоя - "центр".
Построим фазовый портрет системы в плоскости (x, y).

Построим фазовый портрет все системы в плоскости (N₁, N₂).

Полуоси препятствуют дальнейшему увеличению траектории.
Ось N₁ как фазовая траектория имеет смысл развития жертвы в отсутствие хищника - неограниченный рост. Фазовая траектории, лежащая на оси N₂, соответствует гибели хищника в отсутствие жертвы, движение - к точке покоя.