
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о представлении сходящейся числовой последовательности.
Теорема о представлении сходящейся числовой последовательности. Тэарэма (пра выяўленне збежнай лікавай паслядоўнасці). Для таго каб лікавая паслядоўнасць □ (Неабходнасць) Няхай (Дастатковасць) Няхай
Предел частного двух сходящихся числовых последовательностей. (Ліміт дзелі дзвюх збежных лікавых паслядоўнасцяў) Калі □ Маем Предельный переход в неравенствах. Тэарэма. (пра лімітавы пераход у няроўнасцях). Калі, пачынаючы з некаторага нумара, для элементаў дзвюх збежных лікавых паслядоўнасцяў □ (ад процілеглага) Няхай (Дастаткова ўзяць
Выкарыстоўваючы па чарзе спачатку правую няроўнасць з (4), затым няроўнасць (2) і, нарэшце, левую няроўнасць з (3), атрымаем
Теорема о сжатой последовательности. Тэарэма (пра сціснутую паслядоўнасць, або прынцып двух міліцыянтаў). Калі і □ Выберам адвольна
Беручы адпаведныя няроўнасці з (6), (5) і (7), атрымаем З гэтых няроўнасцяў вынікае
Критерий сходимости монотонной числовой последовательности. Тэарэма (Крытэр збежнасці манатоннай паслядоўнасці). Для таго каб манатонная паслядоўнасць была збежнаю, неабходна і дастаткова, каб яна была абмежаванаю.
□ Неабходнасць. Абмежаванасць ёсць неабходная ўмова збежнасці ўсякай паслядоўнасці, у тым ліку манатоннай. Дастатковасць. Доказ правядзем для неспадальнай паслядоўнасці
Стабилизация знака непрерывной функции. Тэарэма. Калі функцыя □ Няхай для пэўнасці Непрерывность сложной функции. def: Няхай функцыя Тэарэма. Калі функцыя □ Паколькі функцыя
З непарыўнасці функцыі Калі ў (4) і (2) узяць Непрерывность тригонометрических функций. 1). Функцыя □ Спачатку дакажам, што Возьмем
2). Функцыя Доказ праводзіцца аналагічна на падставе роўнасці
кампазіцыі і роўнасці
3). Функцыі
Теорема о представлении сходящейся числовой последовательности. Тэарэма (пра выяўленне збежнай лікавай паслядоўнасці). Для таго каб лікавая паслядоўнасць □ (Неабходнасць) Няхай (Дастатковасць) Няхай
|
||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.241.82 (0.016 с.) |
 мела лімітам лік
мела лімітам лік  , неабходна і дастаткова, каб
, неабходна і дастаткова, каб  , дзе
, дзе  ёсць бясконца малая паслядоўнасць.
ёсць бясконца малая паслядоўнасць. і
і  , то лікавая паслядоўнасць
, то лікавая паслядоўнасць 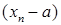 таксама (бмп), г.зн.
таксама (бмп), г.зн.  і
і  , то
, то 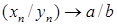 .
.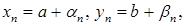 дзе
дзе  – бясконца малыя паслядоўнасці. Таму
– бясконца малыя паслядоўнасці. Таму  . З уласцівасцяў бясконца малых паслядоўнасцяў вынікае, што
. З уласцівасцяў бясконца малых паслядоўнасцяў вынікае, што  ёсць (бмп). Пакажам, што лікавая паслядоўнасць
ёсць (бмп). Пакажам, што лікавая паслядоўнасць  – абмежаваная. Паколькі
– абмежаваная. Паколькі  і
і  , то для
, то для 
 . Далей атрымаем
. Далей атрымаем 
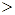

 , г.зн.
, г.зн.  , або
, або  , а таму
, а таму  – абмежаваная лікавая паслядоўнасць(Чаму?). Такім чынам,
– абмежаваная лікавая паслядоўнасць(Чаму?). Такім чынам,  – (бмп). Гэта значыць, мае месца выяўленне
– (бмп). Гэта значыць, мае месца выяўленне 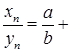 (бмп). На падставе тэарэмы пра выяўленне збежнай паслядоўнасці маем
(бмп). На падставе тэарэмы пра выяўленне збежнай паслядоўнасці маем  . ■
. ■ і
і  праўдзяцца няроўнасці
праўдзяцца няроўнасці  , то ліміты гэтых паслядоўнасцяў праўдзяць няроўнасць
, то ліміты гэтых паслядоўнасцяў праўдзяць няроўнасць  .
. , але
, але  . Возьмем лік
. Возьмем лік  настолькі малы, каб праўдзілась няроўнасць
настолькі малы, каб праўдзілась няроўнасць  . (2)
. (2) .) Паколькі
.) Паколькі  , што раўназначна няроўнасцям
, што раўназначна няроўнасцям  (3)
(3) . (4)
. (4) , адкуль вынікае, што
, адкуль вынікае, што 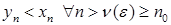 ■
■ мае месца няроўнасць
мае месца няроўнасць  (5)
(5) , то і
, то і  .
. – збежныя, то
– збежныя, то 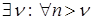 праўдзяцца няроўнасці
праўдзяцца няроўнасці  . (7)
. (7) .
. , г.зн.
, г.зн.  , г.зн.
, г.зн.  . Паколькі паслядоўнасць ёсць абмежаваная, то па тэарэме пра межы лікавая паслядоўнасць
. Паколькі паслядоўнасць ёсць абмежаваная, то па тэарэме пра межы лікавая паслядоўнасць  мае дакладную верхнюю мяжу. Няхай
мае дакладную верхнюю мяжу. Няхай  . Пакажам, што
. Пакажам, што  ёсць ліміт лікавай паслядоўнасці
ёсць ліміт лікавай паслядоўнасці 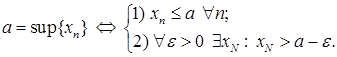 Паколькі паслядаўнасць
Паколькі паслядаўнасць  Такім чынам,
Такім чынам,  , або
, або  . Гэта і азначае, што
. Гэта і азначае, што  ■
■ вызначана ў акрузе пункта
вызначана ў акрузе пункта  , непарыўная ў пункце
, непарыўная ў пункце  , то існуе акруга пункта
, то існуе акруга пункта 
 .
. . З прычыны непарыўнасці
. З прычыны непарыўнасці 



 , адкуль вынікае, што
, адкуль вынікае, што  . Выпадак
. Выпадак  разглядаецца аналагічна (выбіраецца
разглядаецца аналагічна (выбіраецца  ) ■
) ■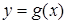 вызначана на
вызначана на  , а функцыя
, а функцыя  вызначана на
вызначана на  , прычым
, прычым  . Тады функцыю, якая
. Тады функцыю, якая  набывае значэнне
набывае значэнне  , называюць складанай функцыяй (або кампазіцыяй, або суперпазіцыяй) функцый
, называюць складанай функцыяй (або кампазіцыяй, або суперпазіцыяй) функцый  і абазначаюць
і абазначаюць  .
. , а функцыя
, а функцыя  , то складаная функцыя
, то складаная функцыя 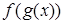 непарыўная ў пункце
непарыўная ў пункце  ёсць непарыўная ў пункце
ёсць непарыўная ў пункце 
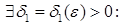

 (1) мае месца
(1) мае месца  . (2)
. (2) існуе
існуе 
 (3) выконваецца няроўнасць
(3) выконваецца няроўнасць  (4).
(4). . Гэта і азначае, што
. Гэта і азначае, што  – непарыўная на
– непарыўная на  .
. Калі
Калі  (гл. §2.7.), а таму
(гл. §2.7.), а таму  Калі
Калі  і пры гэтым
і пры гэтым  тады маем
тады маем 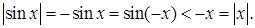 Калі ж
Калі ж  , то з няроўнасці
, то з няроўнасці  вынікае, што
вынікае, што  , маем
, маем для ўсіх
для ўсіх  , якія адпавядаюць няроўнасці
, якія адпавядаюць няроўнасці  Гэта і азначае непарыўнасць сінуса ў пункце
Гэта і азначае непарыўнасць сінуса ў пункце  , а тым самым і на ўсёй лікавай прамой. ■
, а тым самым і на ўсёй лікавай прамой. ■ – непарыўная на
– непарыўная на  , або на падставе тэарэмы пра непарыўнасць
, або на падставе тэарэмы пра непарыўнасць
 – непарыўныя на.абсягу іх існавання як дзель непарыўных функцый.
– непарыўныя на.абсягу іх існавання як дзель непарыўных функцый.


