
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні означення та властивостіСтр 1 из 7Следующая ⇒
Теорія графів
Конспект лекцій з дисципліни „Комп’ютерна дискретна математика” для студентів напряму 6. 050103 „Програмна інженерія”
Львів – 2012
Оглавление 1. Основні означення та властивості 3 3. Способи подання графів. 10
Теорія графів — одна з істотних частин математичного апарату інформатики та кібернетики. У термінах теорії графів можна сформулювати багато задач, пов'язаних із дискретними об'єктами. Такі задачі виникають у проектуванні інтегральних схем і схем управління, у дослідженні автоматів, в економіці й статистиці, теорії розкладів і дискретній оптимізації. Основні означення та властивості Термін „граф" уперше з'явився в книзі видатного угорського математика Д. Кеніга 1936 р., хоча перші задачі теорії графів пов'язані ще з іменем Л. Ейлера (XVIII ст.). Простим графом називають пару G = (V, Е), де V — непорожня скінченна множина елементів, називаних вершинами, Е — множина невпорядкованих пар різних елементів із V. Елементи множини називають ребрами.
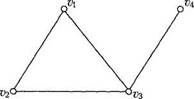
Приклад 3.1. На рис. 3.1 зображено простий граф G з множиною вершин V={v1, v2, v3, v4,} і множиною ребер Е невпорядковані пари різних вершин {{ v1, v2}, { v1, v3 }, { v2, v3 }, { v3, v4}}.
Рис. 3.1. Приклад графу Говорять, що ребро {и, v} з'єднує вершини и та v. Оскільки Е — множина, то в простому графі пару вершин може з'єднувати не більше ніж одне ребро. Іноді розглядають графи, у яких дві вершини можуть бути з'єднані більше ніж одним ребром. Так виникає поняття мультиграфа. Мультиграфом називають пару (V, Е), де V — скінченна непорожня множина вершин, а Е — сім'я невпорядкованих пар різних елементів множини V. Тут застосовано термін „сім'я" замість поняття „множина", бо елементи в Е (ребра) можуть повторюватись. Ребра, що з'єднують одну й ту саму пару вершин, називають кратними (або паралельними). Окрім кратних ребер розглядають також петлі, тобто ребра, які з'єднують вершину саму із собою. Псевдографом називають пару (V, Е), де V — скінченна непорожня множина вершин, а Е — сім'я невпорядкованих пар не обов'язково різних вершин. Приклад 3.2. На рис. 3.2 зображено мультиграф (рис. 3.2, а) і псевдограф (рис. 3.2, б).
Рис. 3.2. Приклад мультиграфу Розглянуті три типи графів називають неорієнтованими. Псевдограф — це най-загальніший тип неорієнтованого графа, бо він може містити петлі й кратні ребра. Мультиграф — це неорієнтований граф, який може містити кратні ребра, але не може містити петель. Нарешті, простий граф — це неорієнтований граф без кратних ребер і без петель.
Розглядають також орієнтовані графи. Орієнтованим графом називають пару (V, Е), де V — скінченна непорожня множина вершин, а Е — множина впорядкованих пар елементів множини V. Елементи множини Е в орієнтованому графі називають дугами (чи орієнтованими ребрами). Дугу (v, v) називають петлею. Приклад 3.3. На рис. 3.3 зображено орієнтований граф із множиною вершин V= {v1, v2, v3, v4, v4} і множиною дуг E={(v2, v1), (v2, v3), (v3, v2), (v3, v4), (v4, v3), (v4, v5), (v5, v5)}.
Зазначимо, що дуга — це впорядкована пара вершин (записують у круглих дужках), тому в графі на рис. 3.3 дуги (v2, v3) та (v3, v2) різні. На рисунках дуги позначають стрілками. Орієнтованим мультиграфом називають пару (V, E), де V — скінченна непорожня множина вершин, а E — сім'я впорядкованих пар елементів множини V.
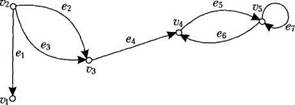
Отже, елементи (дуги) в E в разі орієнтованого мультиграфа можуть повторюватись, такі дуги називають кратними. Зауважимо, що кратні дуги з'єднують одну пару вершин і однаково напрямлені. Приклад 3.4. На рис. 3.4 наведено приклад орієнтованого мультиграфа. Дуги е2 та е3 — кратні, а дуги е5, е6 — ні.
Рис. 3.4. Орієнтований мультиграф Надалі ми будемо використовувати термін „граф" для опису довільних графів — орієнтованих і неорієнтованих, із петлями та кратними ребрами чи без них, а термін „неорієнтований граф" або „псевдограф" — для довільного неорієнтованого графа, який може мати кратні ребра й петлі. Означення різних типів графів зведено в табл. 3.1. Таблиця 3.1
Дві вершини и та v в неорієнтованому графі G називають суміжними, якщо {и, v} — ребро: {и, v) Є Е. Якщо є = {и, v } — ребро, то вершини и та v називають його кінцями. Два ребра називають суміжними, якщо вони мають спільний кінець. Вершину v та ребро є називають інцидентними, якщо вершина v — кінець ребра e. Зазначимо, що суміжність — це зв'язок між однорідними елементами графа, а інцидентність — зв'язок між його різнорідними елементами. Степінь вершини в неорієнтованому графі — це кількість інцидентних їй ребер, причому петлю враховують двічі. Степінь вершини v позначають deg(v). Якщо deg(v) = 0, то вершину v називають ізольованою; якщо deg (v) = 1 — висячою, або кінцевою.
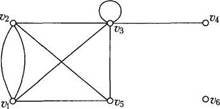
Приклад 3.5. У неорієнтованому графі на рис. 3.5 степені вершин такі: deg(v1) = 4, deg(v2) = 4, deg(v3) = 6, deg(v4) = 1, deg(v5) = 3, deg(v6) = 0. Отже, вершина v6 — ізольована, а v4 - висяча.
Рис. 3.5. Степені неорієнтованого графу Зв'язок між степенями вершин неорієнтованого графа та кількістю його ребер дає така теорема. ТЕОРЕМА 3.1. Нехай G = (V, Е) — неорієнтований граф з те ребрами. Тоді
Доведення. Додавання кожного нового ребра додає по одиниці до степенів двох вершин або двійку до степеня однієї вершини в разі петлі. ТЕОРЕМА 3.2. Неорієнтований граф має парну кількість вершин непарного степеня. Доведення. Позначимо як V1 множину вершин парного степеня, як V2 – непарного, а як m – кількість ребер графа. Тоді
Отже, Σ deg(v) – v Є V2 парне число. Сума непарних чисел парна тоді й лише тоді, коли кількість доданків парна. Якщо в орієнтованому мультиграфі G = (V, Е), (и, v) є Е, то вершину и називають початковою (ініціальною), а вершину v — кінцевою (термінальною) вершиною дуги e = (и, v). Петля має початок і кінець в одній і тій самій вершині. Для орієнтованого графа означення степеня вершини інше. В орієнтованому мультиграфі напівстепенем входу вершини v називають кількість дуг, для яких вершина v кінцева, позначають deg+(v). Напівстепенем виходу вершини v називають кількість дуг, для яких вершина v початкова, позначають deg-(v). Приклад 3.6. Для графа, зображеного на рис. 3.6, напівстепені вершин такі: deg─(v1) = 0, deg+(v,) = 1, deg─(v2) = 2, deg+(v2) = 0, deg─(v3) = 1, deg+(v3) = 2.
ТЕОРЕМА 3.3. Нехай G = (V, Е) — оріє'нтований мультиграф, який має т дуг. Тоді
Простий граф H = (W, F) називають пі дграфом простого графа G = (V, E), якщо W e V, Fе Е. Пі дграф Н називають каркасним (або фактором), якщо W = V. Якщо W ¥ V, a F — множина вcix ребер з Е, які мають кінці в W, то підграф Н називають породженим (або ін дукованим) множиною W i позначають як G(W). Приклад 3.7. На рис. 3.7 зображено граф G та три його підграфа Ни Н 2, Н3, серед яких Н2 породжений, а Н3 — каркасний.
Рис. 3.7 Об'єднанням двох простих графів G1 = (V1, Et) та G2 = (V2,E2) називають такий простий граф G = (V, Е), що V = Vx u V2, E = Et u E2. Приклад 3.8. На рис. 3.8 зображено приклад об'еднання двох простих графів. Знаки „U" та „ = " тут мають символічний зміст.
Рис. 3.8 Об’єднання графів Надалі значну увагу буде приділено алгоритмам на графах, тому дамо деякі означення, що стосуються алгоритмів. Під час аналізу алгоритму нас буде цікавити передусім його складність, під якою розуміємо час виконання відповідної програми на комп'ютері Зрозуміло, що цей показник суттєво залежить від типу комп'ютера. Щоб висновки про складність були достатньо універсальними, будемо вважати, що вci обчислення виконуються на якомусь ідеалізованому комп'ютері. Цим питанням повністю присвячено розділ 10, а тут лише коротко окреслимо суть справи.
Означимо складністьалгоритму розв'язування задачі як функцію f, яка кожному невід'ємному цілому числу п ставить у відповідність час роботи f(n) алгоритму в найгіршому випадку на входах довжиною п. Час роботи алгоритму вимірюють у кроках (операціях), виконуваних на ідеалізованому комп'ютері Наприклад, якщо алгоритм приймає як вхідні дані довільний граф G = (V, E), то піддовжиною входу можна розуміти │V│ чи max{ |V|, |Е|}. Аналіз ефективності алгоритмів полягає в з'ясуванні того, як швидко зростає функція f(n) з i збільшенням п. Для порівняння швидкості зростання двох функцій f(n) i g(n) (з невід'ємними значеннями) використовують такі позначення: ♦ f(n ) = O(g(n)) означає, що існують додатна стала с та натуральне число nтакі, що f(n) < cg(n) для Bcix n > n0. ♦ f (n) = Q(g(n)) означає, що існують додатна стала с та натуральне число nтакі, що f(n) > cg(n) для Bcix n > n0. Для аналізу ефективності алгоритмів використовують О-символіку. Вираз складність алгоритму дорівнює (становить) O(g(n)) має саме такий зміст, як у наведеному вище означенні. Зокрема, складність O(1) означає, що час роботи відповідного алгоритму не залежить від довжини входу. Алгоритм зі складністю О(п), де п — довжина входу, називають ліні йним. Такий алгоритм для переважної більшості задач найліпший (за порядком) щодо складності. Алгоритм, складність якого дорівнює О(р(п)), де р(п) — поліном, називають поліноміальним. Часто замість О(р(п)) пишуть О(пa), де а — константа. Особливу роль поліноміальних алгоритмів описано в розділі 10. Тут лише зазначимо, що всі задачі дискретної математики, які вважають важкими для алгоритмічного розв'язування, нині не мають поліноміальних алгоритмів. Крім того, поняття «поліноміальний алгоритм» — це найпоширеніша формалізація поняття «ефективний алгоритм». Алгоритми, часова складність яких не піддається подібній оцінці, називають експоненціальними. Більшість експоненціальних алгоритмів — це просто варіанти повного перебору, а поліноміальні алгоритми здебільшого можна побудувати лише тоді, коли вдається заглибитись у суть задачі Задачу називають важкорозв'язною, якщо для її розв'язання не іcнyє поліноміального алгоритму. Рис. 3.12. Колеса Простий граф, вершини якого зображають yсі 2 бітові рядки довжиною п, називають п - вимірним кубом і позначають Qп. Дві вершини в Q п з'єднано ребром тоді и лише тоді, коли бітові рядки, які їx подають, відрізняються точно в одному біті.
Граф Qn+1 можна отримати з двох графsв Q з'єднавши ребрами їxнi однаково позначені вершини. Після цього до бітових рядків у вершинах одного з графів Qn зліва дописують 0, другого — 1. Приклад 3.13. На рис. 3.13 зображено графи Q1, Q2 та Qз
Рис. 3.13 N-вимірні куби Способи подання графів Найзрозуміліший і корисний для людини cпоcі6 подання (зображення) графів — це рисунок на площині у вигляді точок і ліній, які з'єднують ці точки. Проте цей cпoсі6 подання абсолютно непридатний, якщо потрібно розв'язувати на комп'ютері задачі з графами. Розглянемо декілька інших способів подання графів для двох найважливіших графів: простого й орієнтованого (рис. 3.15).
Рис. 3.15 Простий та орієнтований граф
Матрицю, кожний елемент якої дорівнює 0 чи 1, називають булевою. 3.3.1. Матриця інцидентності Нехай G=(V,E) — простий граф із множиною вершин V={v1 , v 2,..., vn } і множиною ребер Е - {е1, е2,..., ет). Матрицею інцидентності графа G, яка відповідає заданій нумерації вершин і ребер, називають булеву п×т матрицю М з елементами mij (і = 1,..., п; j = 1,..., m), де mij = 1, якщо вершина vi та ребро ei, інцидентні, mij = 0 у протилежному випадку. Приклад 3.14. Для неорієнтованого графа, зображеного на рис. 3.14, матриця інцидентності має вигляд
Отже, для простого графа в матриці інцидентності в кожному стовпці точно дві одиниці, і немає однакових стовпців. Матрицю інцидентності можна використовувати й для подання мультиграфа. Тоді з'являться однакові стовпці (вони відповідають кратним ребрам). Для подання псевдографа, якщо в ньому є петлі, у відповідних позиціях матриці ставимо 2 (у цьому разі матриця інцидентності не булева). За допомогою матриці інцидентності можна подавати й орієнтовані графи. Для таких графів вона також не булева. Нехай G = (V, E) — орієнтований граф із множиною вершин V={v1,v 2,..., vn } і множиною дуг Е= {е1 е2,..., ет). Матрицею інцидентності орієнтованого графа G, яка відповідає заданій нумерації вершин і дуг, називають п×т матрицю М з елементами mij (і = 1,..., п; j = 1,..., m), де
Приклад 3.15. Для орієнтованого графа, зображеного на рис. 3.15, матриця інцидентності має вигляд
З алгоритмічного погляду матриця інцидентності — це, мабуть, найгірший спосіб подання графа, який тільки можна собі уявити [23]. По-перше, для цього потрібно п×т комірок пам'яті, більшість із яких зайняті нулями. По-друге, доступ до інформації незручний. Щоб отримати відповідь на елементарні питання (наприклад, чи існує дуга (vi, vj ), до яких вершин ведуть дуги з vi), у найгіршому випадку потрібно перебрати всі стовпці матриці, тобто виконати т кроків. Матриця суміжності Нехай G = (V, Е) — простий граф, │v│ =п. Припустимо, що вершини графа G занумеровані: v1 v2, -, v„. Матрицею суміжності графа G (яка відповідає даній нумерації вершин) називають булеву п×п матрицю А з елементами aij (i,j= 1,..., п), де
Приклад 3.16. Матриця суміжності для графа, зображеного на рис. 3.14, має вигляд
Цілком очевидно, що для неорієнтованого графа aij = aji, тобто матриця суміжності симетрична. Більше того, позаяк у простому графі немає петель, то для нього в матриці суміжності aii = 0 (I = 1,..., п). Матрицю суміжності можна використовувати також для подання псевдографа. Тоді це не булева матриця: елемент аij дорівнює кількості ребер, що з'єднують vt та vj. Петлю у вершині vi подають значенням діагонального елемента ай = 1. Для подання орієнтованих графів також використовують матрицю суміжності. Це булева п×п матриця А з елементами аij (i,j= 1,..., п), де
Приклад 3.17. Матриця суміжності для графа, зображеного на рис. 3.15, має вигляд. Зазначимо, що матриця суміжності орієнтованого графа, загалом кажучи, несиметрична. Матрицю суміжності можна використовувати й для подання орієнтованого мультиграфа. У такому разі це не булева матриця: елемент aij дорівнює кількості дуг, які мають vi початковою вершиною, а v j — кінцевою. Велика перевага матриці суміжності як способу подання графа — швидкий доступ до інформації: за один крок можна одержати відповідь на питання, чи існує ребро (дуга) з vi y vj.Вада полягає в тому, що незалежно від кількості ребер обсяг пам'яті становить п2 комірок. Як іще один аргумент проти використання матриці суміжності можна навести теорему про кількість кроків алгоритму, який на основі матриці суміжності перевіряє якусь властивість простого графа (див. підрозділ 3.5, теорему 3.9). Нарешті, розглянемо ще два способи подання графів у пам'яті комп'ютера. Будь-яку скінченну послідовність довільних елементів будемо називати списком, а кількість елементів списку — його довжиною.
Ейлерів цикл у графі Початок теорії графів як розділу математики пов’язують із задачею про кенінгсберські мости. Сім мостів міста Кенігсберга (нині Калінінград у Росії) було розміщено на річці Прегель так, як зображено на рис 3.30. Чи можна починаючи з якоїсь точки міста, пройти через усі мости точно по одному разу й повернутися у початкову точку? Швейцарський математик Л. Ейлер розв’язав цю задачу. Його розв’язання опубліковано 1736 р., було першим явним застосування теорії графів. Ейлер поставив у відповідність плану міста мультиграф G, вершини якого відповідають чотирьом частинам A, B, C, D міста, а ребра мостам. Цей граф зображено на рис. 3.31.
Рис 3.30. Кенігсбергські мости та їх модель за допомогою графу
Рис 3.30. Модель кенігсбергських мостів за допомогою графу
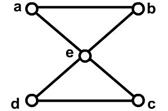
Отже, задачу про кенінгсберські мости мовою теорії графів можна сформулювати так: чи існує в мультиграфі G простий цикл, який містить усі ребра цього мультиграфа? Ейлер довів нерозв’язність задачі про кенінгсберські мости. Нагадуємо, що в простому циклі ребра не повторюються, а вершини можуть повторюватись. Ейлеровим циклом у зв’язному мультографі G називають простий цикл, який містить усі ребра графа, ейлеревим шляхом – простий шлях, що містить усі ребра графа. Приклад 3.31. На рис. 3.32 проілюстровано концепцію ейлеревих циклів і шляхів. Граф G1 має ейлерів цикл, наприклад, a, e, c, d, e, b, a; граф G3 не має ейлеревого циклу, але має ейлерів шлях: a, c, d, e, b, d, a, b; граф G2 не має ні ейлеревого циклу, ні ейлеревого шляху.
Існує простий критерій (необхідна й достатня умова) для виявлення того, чи має граф ейлерів цикл. ТЕОРЕМА 3.10. Зв’язний граф G має ейлерів цикл тоді й лише тоді, коли степені всіх його вершин парні. Доведення. Необхідність. Нехай у графі G існує ейлерів цикл. Тоді він проходить через кожну вершину графа і входить до неї по одному ребру, а виходить по іншому. Це означає, що кожна вершина інцидентна парній кількості ребер ейлеревого циклу. Оскільки такий цикл містить усі ребра графа G, то звідси випливає парність степенів усіх його вершин. Достатність. Припустимо тепер, що всі вершини графа G мають парний степінь почнемо шлях Р1 із довільної вершини V1 і продовжемо його наскільки це можливо, вибираючи щоразу нове ребро. Позаяк степені усіх вершин парні, то, увійшовши у будь-яку вершину, відмінну від V1, ми завжди маємо можливість вийти з неї через іще не пройдене ребро. Тому шлях Р1 можна продовжити додавши це ребро. Отже, побудова шляху Р1 завершиться у вершині V1, тобто Р1 обов’язково виявиться циклом. Якщо з’ясується що шлях Р1 містить усі ребра графа G, то це ейлерів цикл. У протилежному випадку вилучемо з G всі ребра типу Р1 і всі вершини, інцидентні лише вилученим ребрам. Отримаємо якийсь зв’язний граф G1. Оскільки Р1 та G мають вершини лише парних степенів,то, очевидно, і граф G1 матиме цю властивість. Окрім того, позаяк граф G зв’язний, то графи Р1 та G1 мають принаймні одну спільну вершину V2. Тепер із вершини V2 побудуємо цикл Р1 в графі G1 аналогічно до того, як ми будували цикл Р1 у графі G. Цикл Р1 на місце вершини V2. Одержимо цикл Р3. Описані побудови показано на рис.3.33
Рис 3.30. Алгоритм Фльорі Цикл Р1 = v1, v4, v3, P2, v1 = v1, v4, v3, v2, v5, v6, v2, v1 ейлерів. Якби він виявився не ейлеревим, то потрібно продовжити аналогічні побудови і отримати ще більший цикл. Цей процес закінчиться побудовою ейлеревого циклу. Зазначимо, що доведення достатності має конструктивний характер: подано алгоритм побудови ейлеревого циклу. Існує і інший алгоритм побудови ейлерового циклу, який дає змогу побудувати цей цикл одразу. Це алгоритм Флері (Fleury). Гамільтонів цикл у графі Шлях x0,x1,…,xn-1,xn у зв’язному графі G = (V, E) називають гамільтоновим шляхом, якщо V = { x0,x1,…,xn-1,xn } і Цикл x0,x1,…,xn-1,xn, x0 (тут n>1) у графі G = (V, E) називають гамільтоновим циклом, якщо x0,x1,…,xn-1,xn, - гамільтонів шлях. Інакше кажучи, гамільтонів цикл і гамільтонів шлях проходять через кожну вершину графа точно один раз (можливо, окрім першої й останньої вершин). Зазначимо, що гамільтонові цикл і шлях, узагалі кажучи, не містять усіх ребер графа. Термін «гамільтонів» у цих означеннях походить від імені відомого ірландського математика У. Гамільтона (W. Hamilton), який 1857 р. запропонував гру «Навколосвітня подорож». Кожній із двадцяти вершин додекаедра (правильного дванадцятигранника, грані якого – п’ятикутники) прописано назву одного з великих міст світу. Потрібно, розпочавши з довільного міста, відвідати решту 19 міст точно один раз і повернутися у початкове місто. Перехід дозволено ребрами додекаедра [52]. Приклад 3.32. Ту саму задачу можна зобразити й на площині (рис. 3.34). Вона зводиться до відшукання в графі гамільтонового циклу. Один із можливих розв’язків показано пунктирними лініями.
Рис 3.31. Розв’язок задачі про всесвітню подорож
Не всі зв’язні графи мають гамільтонів цикл хоча б тому, що такий граф має бути двозв’язним (тобто граф, який має точки з’єднання, не може мати гамільтонового циклу). Приклад графа зображеного на рис. 3.35, свідчить, що двозязності недостатньо для наявності гамільтонового циклу. Незважаючи на зовнішню подібність формулювань задач про існування ейлерового й гамільтонового циклів, ці задачі принципово різні. Використовуючи результати попереднього підрозділу, легко виявити, чи має граф ейлерів цикл, і, якщо має, то побудувати його.
Рис 3.31. Двозв’язний граф, який не має гамільтонового циклу
Ситуація для гамільтонового циклу істотно інша. Відповісти на питання, чи має граф гамільтонів цикл, зазвичай, дуже важко. Вивчення достатніх умов наявності в графі гамільтонового циклу – один із важливих напрямів у теорії графів. Інтуїтивно зрозуміло, що граф із багатьма ребрами, достатньо рівномірно розподіленими, з великою ймовірністю має гамільтонів цикл. Доведемо одну теорему з теорем такого типу. ТЕОРЕМА 3.13 (Г. Дірака, 1952 р.). Якщо для кожної вершини v зв’язного простого графа з n>=3 вершинами виконується нерівність deg(v)>=n/2, то цей граф має гамільтонів цикл. Як знайти гамільтонів цикл або переконатися, що його немає? Очевидний алгоритм, який можна застосувати, - це повний перебір усіх можливостей, тобто n! перестановок усіх вершин графа й перевірок. Зрозуміло що такий спосіб не практичний. Розгляд реального алгоритму бектрекінг відкладемо до наступного розділу (розділ 4.5, приклад 4.15). Для задачі знаходження гамільтонового невідомий ефективний (тобто з поліноміальною складністю) алгоритм розв’язання, і є вагомі підстави вважати, що його не існує. Граф, який містить гамільтонів цикл, часто називають гамільтоновим графом. Алгоритм Дейкстри Наведемо кроки алгоритму. Крок 1. Присвоювання початкових значень. Виконати l(a):=0 та вважати цю мітку постійною. Виконати l(v):= Крок 2. Оновлення міток. Для кожної вершини v є Г(x)\M замінити мітки: l(v):= min{l(v); l(x)+w(x,v)}, тобто оновлювати тимчасові мітки вершин, у які з вершини x іде дуга. Крок 3. Перетворення мітки в постійну. Серед усіх вершин із тимчасовими мітками знайти вершину з мінімальною міткою, тобто знайти вершину v* з умови l(v*) = min{l(v)}, v є T, де T = V\M. Крок 4. Уважати мітку вершини v* постійною і виконати M:=MÈ{v*}; x:=v* (вершину v* включено в множину М). Крок 5. а) Для пошуку шляху від a до z; якщо x = z, то l(z) – довжина найкоротшого шляху від a до z; зупинитись; якщо x!=z, то перейти до кроку 2. б) Для пошуку шляхів від a до всіх інших вершин: якщо всі вершини отримали постійні мітки (включені в множину М) то ці мітки дорівнюють довжинам найкоротших шляхів, зупинитися; якщо деякі вершини мають тимчасові мітки, то перейти до кроку 2. Таблиця 3.4
Ми розглянули задачу відшукання в графі найкоротшого шляху від якоїсь виділеної (початкової) вершини до будь-якої іншої. Розглянемо задачу пошуку в графі найкоротшого шляху між кожною парою вершин. Звичайно, цю загальнішу задачу можна розв'язати багатократним застосуванням алгоритму Дейкстри з послідовним вибором кожної вершини графа як початкової. Проте є й прямий спосіб розв'язання цієї задачі за допомогою алгоритму Флойда. У ньому довжини дуг можуть бути від'ємними, проте не може бути циклів із від'ємною довжиною. Нехай G= (V, E) — орієнтований граф. Нагадаємо, що внутрішні вершини шляху a, x1, x2, xm-u в графі G — х1, х2, …, хm-1. Наприклад, внутрішні вершини шляху а, с, d, а, f, b — с, d, а, f. Пронумеруємо вершини графа цілими числами від 1 до n. Позначимо як В алгоритмі Флойда як початкову беруть матрицю W(0). Спочатку за нею обчислюють матрицю W(1) потім — W(2), і процес повторюють доти, доки за матрицею W(n-1) не буде обчислено матрицю W(n) Розглянемо ідею, на якій ґрунтується алгоритмі Флойда. Припустимо, що відомі.
1. Найкоротший шлях із вершини і у вершину k, у якому як внутрішні використано лише перші (k-1) вершин. 2. Найкоротший шлях із вершини k у вершину j, у якому як внутрішні використано лише перші (k - 1) вершин. 3. Найкоротший шлях із вершини і у вершину j, у якому як внутрішні використано лише перші (k - 1) вершин. Оскільки за припущенням граф G не містить циклів із від'ємною довжиною, то один із двох шляхів — шлях із п. 3 чи об'єднання шляхів із пп. 1 і 2 — найкоротший шлях із вершини і у вершину j, у якому як внутрішні використано лише перші (k - 1) вершин. Отже,
Зі співвідношення (3.1) видно, що для обчислення елементів матриці w
Алгоритм Флойда Наведемо кроки алгоритму. Крок 1. Присвоювання початкових значень. Пронумерувати вершини графа Gцілими числами від 1 до n. Побудувати матрицю W(0)= W, задавши кожний її (i,j)-елемент такий, що дорівнює вазі дуги, котра з'єднує вершину і з вершиною j. Якщо в графі G ці вершини не з'єднано дугою, то виконати Крок 2. Цикл. Для k, що послідовно набуває значення 1, 2, …, п, визначити за елементами матриці W(k-1) елементи матриці W(k) використовуючи рекурентне співвідношення (3.1). Після закінчення цієї процедури (і,j) - елемент матриці W(n) дорівнює довжині найкоротшого шляху з вершини і у вершину j. Якщо під час роботи алгоритму для якихось k й і виявиться, що Якщо заздалегідь відомо, що в графі Є немає циклів із від'ємною довжиною, то обсяг обчислень можна дещо зменшити. У цьому разі для всіх і та всіх k має бути Приклад 3.34. Знайти найкоротші шляхи між усіма парами вершин орієнтованого графа на рис. 3.38.
Рис. 3.38 Граф до прикладу 3.34
Нижче наведено результати виконання кожної з чотирьох
W(0)= W=
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 967; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.59.231 (0.126 с.) |

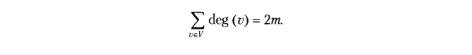 Це твердження стосується будь-якого неорієнтованого графа, зокрема з петлями та кратними ребрами.
Це твердження стосується будь-якого неорієнтованого графа, зокрема з петлями та кратними ребрами.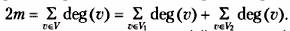

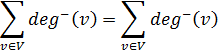

















 для
для  .
.

 для всіх v!=a вважати ці мітки тимчасовими. Виконати x:=a, M:={a}.
для всіх v!=a вважати ці мітки тимчасовими. Виконати x:=a, M:={a}.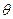 (вершини, з яких у дану вершину заходить найкоротший шлях)
(вершини, з яких у дану вершину заходить найкоротший шлях)

 довжину найкоротшого шляху з вершини і у вершину j, у якому як внутрішні можуть бути лише перші k вершин графа G. Якщо між вершинами і тa j не існує жодного такого шляху, то умовно вважатимемо, що
довжину найкоротшого шляху з вершини і у вершину j, у якому як внутрішні можуть бути лише перші k вершин графа G. Якщо між вершинами і тa j не існує жодного такого шляху, то умовно вважатимемо, що  . Зі сказаного випливає, що
. Зі сказаного випливає, що  — це вага дуги (ij), а якщо такої дуги немає, то
— це вага дуги (ij), а якщо такої дуги немає, то  дорівнює довжині найкоротшого шляху з вершини і у вершину j. Позначимо як W
дорівнює довжині найкоротшого шляху з вершини і у вершину j. Позначимо як W  nxn матрицю, (і, j)-й елемент якої дорівнює
nxn матрицю, (і, j)-й елемент якої дорівнює  (3.1)
(3.1) . Тепер ми можемо формально описати алгоритм Флойда для знаходження в графі найкоротших шляхів між усіма парами вершин.
. Тепер ми можемо формально описати алгоритм Флойда для знаходження в графі найкоротших шляхів між усіма парами вершин.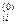 := 0.
:= 0. < 0, то в графі G існує цикл із від'ємною довжиною, який містить вершину і. Тоді роботу алгоритму потрібно припинити.
< 0, то в графі G існує цикл із від'ємною довжиною, який містить вершину і. Тоді роботу алгоритму потрібно припинити.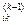 =
= 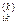 ,
,  =
= 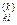 які випливають із того, що коли немає циклів із від'ємною довжиною, вершина k не може бути внутрішньою в будь-яких найкоротших шляхах, котpі починаються чи закінчуються в самій вершині k. Отже, обчислюючи матрицю немає потреби переобчислювати елементи k-го рядка й k-го стовпця матриці W(k-1). Отже, у матриці W(k) за формулою (3.1) потрібно обчислювати лише k2 – З × п + 2 елементи. Очевидно, що складність алгоритму Флойда становить 0(п3). Щоб після закінчення його роботи можна було швидко знайти найкоротший шлях між будь-якою парою вершин, на k-й ітерації разом із матрицею W(k) побудуємо матрицю
які випливають із того, що коли немає циклів із від'ємною довжиною, вершина k не може бути внутрішньою в будь-яких найкоротших шляхах, котpі починаються чи закінчуються в самій вершині k. Отже, обчислюючи матрицю немає потреби переобчислювати елементи k-го рядка й k-го стовпця матриці W(k-1). Отже, у матриці W(k) за формулою (3.1) потрібно обчислювати лише k2 – З × п + 2 елементи. Очевидно, що складність алгоритму Флойда становить 0(п3). Щоб після закінчення його роботи можна було швидко знайти найкоротший шлях між будь-якою парою вершин, на k-й ітерації разом із матрицею W(k) побудуємо матрицю  (k) =[
(k) =[ 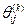 ]. Спочатку беремо
]. Спочатку беремо  :=і для всіх і,j= 1, …, п,
:=і для всіх і,j= 1, …, п,  ;
;  := 0. Далі, на к-й ітерації візьмемо
:= 0. Далі, на к-й ітерації візьмемо  , якщо
, якщо  =
=  і
і  , якщо
, якщо  =
=  . Отже,
. Отже,  ] відіграє ту саму роль, що й вектор
] відіграє ту саму роль, що й вектор 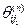 , j3=
, j3=  , ….
, ….





