
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи управления запасами при нескольких уровнях цен ⇐ ПредыдущаяСтр 4 из 4
Рассмотрим простейшую модель управления запасами, в которой предприниматель должен поставлять или продавать своим клиентам Такая модель уже была рассмотрена ранее, но в этой модели имеется «скидка на количество» закупаемого продукта. Очень часто в задачах управления запасами при закупке товаров большими партиями вводятся скидки. Эти скидки могут иметь различный вид. Рассмотрим случай, когда скидки вводятся следующим образом. Пусть заданы числа Подобные скидки на размер заказа будем называть оптовыми, так как скидка начисляется на каждую единицу закупаемого товара. Введение оптовых скидок затрудняет определение оптимального размера заказа на пополнение. Рассмотрим случай, когда спрос Если
Величина Тогда получаем, что
Для Можно считать, что это выражение для Представим эту ситуацию графически.
Рис. 2.2.2. Графическое представление функции Задача определения оптимального размера состоит в определении самой нижней точки на кривой с разрывами.
Это можно сделать, вычислив сначала все значения Существуют также и другие виды скидок. К сожалению, все виды скидок рассмотреть в данном курсе нет возможности. На следующей лекции мы рассмотрим еще один важный вид скидки, которая называется дифференциальной скидкой на размер заказа. Задачи управления запасами при нескольких уровнях цен. Дифференциальные скидки. Задачи управления запасами при нескольких уровнях цен Дифференциальные скидки.
Как уже отмечалось на предыдущей лекции, сейчас мы переходим к рассмотрению другого весьма важного вида скидки, которая называется дифференциальной скидкой на размер заказа. Дифференциальная скидка состоит в том, что если размер заказа колеблется от 1 до
где Таким образом, если дефицит не допускается, средние годовые издержки
где Графически общие издержки на закупку продукции могут быть представлены в следующем виде
Рис. 2.2.3. Графическое представление функции
Можно представить, что Вычисление оптимального значения
Это следует из того, что результирующая кривая общих издержек непрерывна, т.е. Если имеется
Рис. 2.2.4. Графическое представление функции
Поэтому вычисление минимального значения функции издержек в этом случае производится следующим образом. Вычисляется оптимальное значение
где величина
Откуда получаем
Для каждого
|
||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 399; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.202.187 (0.017 с.) |
 единиц продукции равномерно в течение времени
единиц продукции равномерно в течение времени  . Спрос на продукцию является известным и фиксированным. Нехватка продукции считается недопустимой, т. е. штраф за нехватку бесконечен
. Спрос на продукцию является известным и фиксированным. Нехватка продукции считается недопустимой, т. е. штраф за нехватку бесконечен  .
. . Причём
. Причём  и
и  . Если размер закупки равен
. Если размер закупки равен  и
и 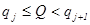 , то стоимость закупки каждой единицы товара из этой партии равна
, то стоимость закупки каждой единицы товара из этой партии равна  и
и  (
( ). Таким образом, стоимость закупленной партии товара размером
). Таким образом, стоимость закупленной партии товара размером  и
и 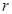 постоянный, известны стоимость хранения единицы товара
постоянный, известны стоимость хранения единицы товара 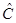 и
и  стоимость закупки. Дефицит товара не допускается.
стоимость закупки. Дефицит товара не допускается.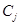 является стоимостью единицы товара, то общие издержки на закупку, хранение и доставку товара могут быть представлены в виде
является стоимостью единицы товара, то общие издержки на закупку, хранение и доставку товара могут быть представлены в виде

 Рис. 2.2.1. График затрат на закупки продукта при оптовых скидках.
Рис. 2.2.1. График затрат на закупки продукта при оптовых скидках. ,
, 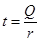 и
и 

 величина
величина  представляет общие издержки по созданию и хранению запасов в течение времени
представляет общие издержки по созданию и хранению запасов в течение времени  . Следует отметить, что теперь возникает необходимость включить стоимость самого товара в выражение переменных издержек, так как стоимость изделия зависит от размера заказа, т.е. от стратегии управления.
. Следует отметить, что теперь возникает необходимость включить стоимость самого товара в выражение переменных издержек, так как стоимость изделия зависит от размера заказа, т.е. от стратегии управления. кривых издержек, соответствующих каждому значению
кривых издержек, соответствующих каждому значению  они не существуют и отличаются только постоянным слагаемым
они не существуют и отличаются только постоянным слагаемым  .
.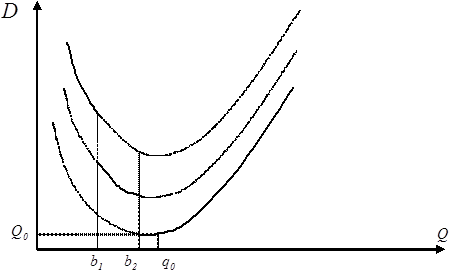
 , в которых достигают минимума соответствующие кривые
, в которых достигают минимума соответствующие кривые  , то проверяются граничные точки
, то проверяются граничные точки  и
и  и из них выбирается та граничная точка, в которой
и из них выбирается та граничная точка, в которой  , которое и принимается в качестве решения.
, которое и принимается в качестве решения. , то стоимость единицы товаров составляет
, то стоимость единицы товаров составляет 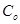 . При размере заказа от
. При размере заказа от  до
до  стоимость составляет
стоимость составляет  (
( ) и т. д. Общие издержки
) и т. д. Общие издержки 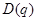 на закупку
на закупку 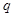 изделий при
изделий при  могут быть представлены как
могут быть представлены как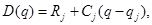


 ,
, 
 ,
, 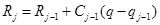
 и для всех
и для всех 
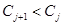 .
. при
при 
 ,
,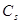 - стоимость запуска в производство или оформление и доставка одной партии товаров,
- стоимость запуска в производство или оформление и доставка одной партии товаров,  - количество закупок. По аналогии с результатами предыдущего пункта
- количество закупок. По аналогии с результатами предыдущего пункта  .
.
 =
=  изломов на кривой издержек, то имеется (
изломов на кривой издержек, то имеется (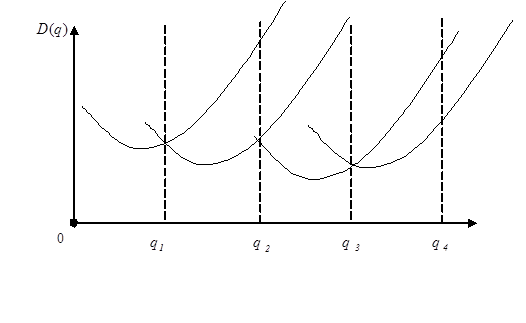
 для каждой кривой
для каждой кривой  ,
,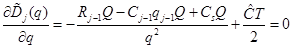 .
. .
. , определяем значение
, определяем значение  и из этих значений выбираем минимальное.
и из этих значений выбираем минимальное.


