Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормированное уравнение плоскости. Расстояние от точки до плоскости ⇐ ПредыдущаяСтр 3 из 3
Пусть - декартова система координат, - произвольная плоскость. Проведем через точку Если
Пусть
Из (4.11), (4.12) и (4.13) получим:
Уравнение (4.14) называется нормированным уравнением плоскости (в 4(.14) Приведем без доказательства следующее утверждение. Теорема 3. Расстояние от точки
Замечание. Для того чтобы от общего уравнения плоскости (4.16) перейти к нормированному уравнению (4.14), нужно обе части (4.16) умножить на нормирующий множитель Действительно, уравнения (4.16) и (4.14) определяют одну и ту же плоскость в том и только в том случае, когда все четыре коэффициента пропорциональны, т.е. найдется такое, что Из первых трех равенств получим
Из равенства следует, что Пример 3. Найти расстояние от точки Найдем нормирующий множитель
Прямая линия в пространстве Определение 4. Пусть Пусть - произвольная декартова система координат, - произвольная прямая,
Уравнения (4.17) называются каноническими уравнениями прямой, проходящей через точку и имеющей в качестве направляющего вектор. Обозначим в (4.17) общее отношение через
Так как, то хотя бы одно из чисел Соотношения (4.18) при называются параметрическими уравнениями прямой, проходящей через точку и имеющей в качестве направляющего вектор.
Замечание. Линию в пространстве естественно рассматривать как пересечение двух поверхностей, т.е. как совокупность точек, находящихся одновременно на двух поверхностях. Если
определяет линию. Пусть: и:, не параллельна и не совпадает с ней. Тогда система уравнений
определяет линию пересечения и, т.е. прямую. Таким образом, система (4.20) – задание прямой как линии пересечения двух плоскостей и. Угол между двумя прямыми в пространстве и между прямой и плоскостью Определение 5. Углом между прямыми
Пусть: Тогда в частности Отметим еще один частный случай:
Определение 6. Углом между прямой и плоскостью называется острый угол между прямой и ее проекцией на плоскость (рис. 4.8). Пусть - произвольная плоскость, - произвольная прямая, не перпендикулярная, :, :. Из определения 6
Частные случаи: 1) 2)
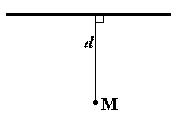
Вопрос. Расстояние между точкой и прямой на плоскости Определение. Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.
Формула для вычисления расстояния от точки до прямой на плоскости Если задано уравнение прямой Ax + By + C = 0, то расстояние от точки M(Mx, My) до прямой можно найти, используя следующую формулу
Примеры задач на вычисление расстояния от точки до прямой на плоскости Пример 1. Найти расстояние между прямой 3x + 4y - 6 = 0 и точкой M(-1, 3). Решение. Подставим в формулу коэффициенты прямой и координаты точки
Ответ: расстояние от точки до прямой равно 0.6.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 340; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.29.89 (0.014 с.) |
 прямую
прямую  , точку пересечения обозначим
, точку пересечения обозначим  . Возьмем вектор такой, что: приложен к точке О,
. Возьмем вектор такой, что: приложен к точке О,  , направление совпадает с направлением вектора
, направление совпадает с направлением вектора  .
. , направление выберем произвольно (рис. 4.6).
, направление выберем произвольно (рис. 4.6).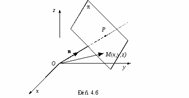
 - углы наклона вектора к осям, и соответственно. Тогда
- углы наклона вектора к осям, и соответственно. Тогда  . Обозначим
. Обозначим  . Имеем
. Имеем ; (4.11)
; (4.11)  ; (4.12)
; (4.12)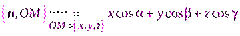 . (4.13)
. (4.13) или
или . (4.14)
. (4.14) - расстояние от начала координат до плоскости, - углы наклона вектора
- расстояние от начала координат до плоскости, - углы наклона вектора  к осям, и соответственно).
к осям, и соответственно). до плоскости равно абсолютной величине результата подстановки координат этой точки в левую часть нормированного уравнения плоскости:
до плоскости равно абсолютной величине результата подстановки координат этой точки в левую часть нормированного уравнения плоскости: . (4.15)
. (4.15) ; знак
; знак 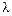 выбирается противоположным знаку
выбирается противоположным знаку  в (4.16).
в (4.16). ,
,  ,
,  ,
,  .
.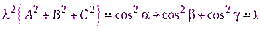

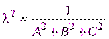 и.
и. (так как
(так как  ), следовательно, и разных знаков.
), следовательно, и разных знаков. до плоскости
до плоскости  .
. . Нормированное уравнение плоскости:
. Нормированное уравнение плоскости: ,
, .
. - произвольная прямая, любой вектор
- произвольная прямая, любой вектор  ,
, 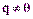 такой, что параллелен, называется направляющим вектором прямой.
такой, что параллелен, называется направляющим вектором прямой. ,
,  – направляющий вектор прямой. Этими условиями полностью определяется положение прямой в пространстве.
– направляющий вектор прямой. Этими условиями полностью определяется положение прямой в пространстве. коллинеарен
коллинеарен . (4.17)
. (4.17) , тогда
, тогда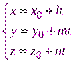 (4.18)
(4.18) ,
,  , либо отлично от нуля. Пусть для определенности
, либо отлично от нуля. Пусть для определенности  . Тогда при
. Тогда при  число
число  пробегает всю ось и
пробегает всю ось и  , и, таким образом,
, и, таким образом,  .
. и
и  - уравнения двух поверхностей, пересечением которых является линия, то система уравнений
- уравнения двух поверхностей, пересечением которых является линия, то система уравнений (4.19)
(4.19) (4.20)
(4.20) и
и  называется любой из двух углов, образуемых двумя прямыми
называется любой из двух углов, образуемых двумя прямыми  и
и  , соответственно параллельными данным и проходящими через одну точку (рис. 4.7).
, соответственно параллельными данным и проходящими через одну точку (рис. 4.7).
 ,:
,:  .
. ,
, .
.
 и
и 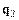 коллинеарны
коллинеарны 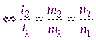 .
. Поэтому
Поэтому .
.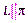 и перпендикулярны
и перпендикулярны 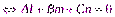 (рис. 4.9);
(рис. 4.9);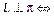 и коллинеарны
и коллинеарны  (рис. 4.10).
(рис. 4.10).