
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Послідовне ввімкнення елементарних ланок
При послідовному з'єднанні ланок вихідна величина попередньої ланки поступає на вхід подальшого. Метод факторизації (LU-перетворення) Розв`язування лінійних рівнянь виконується або прямими, або ітераційними методами. Нижче будуть розглядатися тільки прямі методи розв`язування. До прямих методів відносяться метод Гауса та метод факторизації. Розглянемо метод факторизації (LU-перетворення). Нехай є система лінійних рівнянь:
яку можна записати в матричному вигляді:
Рисунок 7.2. – Метод рухомої області збіжності: а – схема з діодом; б – графічна ілюстрація її розрахунку методом рухомої області збіжності.
Формально цю систему рівнянь можна вирішити, обернувши матрицю А: X=A-1×B.
Однак, така операція трудомістка і вимагає великих затрат машинного часу Тмаш. Чисельне розв`язання систем лінійних рівнянь часто базується на методі Гауса. Він ґрунтується на тому факті, що додавання одного рівняння системи до іншого, помноженого на константу, не змінює рішення. Виключення за Гаусом вимагає виконання n3/3 операцій, де під операцією розуміється комбінація множення та віднімання, а n – порядок матриці. Зворотна підстановка вимагає n2/2 операцій. Однак, кращим методом розв`язування систем лінійних алгебраїчних рівнянь є метод перетворення (розкладу) матриці А на трикутні матриці, або метод LU- перетворення (факторизації). Алгоритм цього методу близький до методу Гауса. Головна перевага методу LU-перетворення в порівнянні з методом Гауса – це можливість більш простого отримання рішень для різноманітних векторів в правій частині системи рівнянь. Припустимо, що матрицю СЛАР можна розкласти на множники A=L·U, де
Тут матриця L є нижньою трикутною, а матриця U – верхньою трикутною. Помітимо, що на головній діагоналі матриці U знаходяться одиниці. Це означає, що визначник матриці А дорівнює добутку діагональних елементів lii матриці L. Припустимо, що ми отримали матриці L та U. Тоді: L×U×X=B Позначимо U×X=Z, тоді ми отримаємо: L×Z=B. Завдяки спеціальній формі матриці L, вектор Z можна легко визначити. Для цього запишемо: l 11z1 = b 1, l 21z2+ l 22z2 = b 2, l 31z3+ l 32z3+ l 33z3 = b 3, l n1z1+ l n2z2+ l n3z3+...+ l nn zn= b n. Звідси одержуємо: z1 = b1/l11, z2 = (b2 - l21z1)/l22, z3 = (b3 – l31z1 – l32z2)/l33, …
Або в загальному вигляді: z1=b1/l11;
Цей процес називається прямим виключенням (прямою підстановкою або прямим ходом). Щоб ці обчислення мали сенс, діагональні елементи lii повинні бути ненульовими. Тепер повернемось до U·X=Z і знайдемо вектор X. x 1+ u 12 x 2+ u 13 x 3+...+ u 1n x n = z1, x 2+ u 23 x 3+...+ u 2n x n = z2, …………………....... x n-1+ u n-1,n x n = zn-1, x n = zn.
Починаючи з останнього рівняння, послідовно знаходимо компоненти вектора X. В загальному вигляді вони визначаються за формулою: xn=zn,
Цей процес називається зворотною підстановкою, або зворотним ходом. Число операцій, необхідних для виконання як прямої підстановки, так і зворотної, дорівнює n2/2, а в сумі для розв`язування СЛАР вимагається n2 операцій. Виведенням формул LU-перетворення займатися не будемо. Наведемо загальні вирази для отримання елементів матриць L та U:
Важливі переваги методу LU-перетворення: 1. Легко обчислюється визначник матриці А:
2. Елементи матриці L та U можуть бути записані на місця елементів матриці А і занесені в ті ж самі осередки пам'яті (запам'ятовувати одиничні елементи на головній діагоналі матриці U немає необхідності). 3. Легко знайти рішення для іншого вектору B у правій частині, тобто не потрібно повторно проводити LU-перетворення, а достатньо провести пряму та зворотну підстановки. 4. Для рівнянь з транспонованою матрицею At X=C рішення знаходиться при тому ж LU-перетворенні. Аналіз таких систем рівнянь необхідний при розрахунку чутливості. Число операцій, необхідних для LU-розкладу, складає (n3/3-n/3) і разом з прямою та зворотною підстановками еквівалентно методу Гауса. Однак він більш прийнятний із-за переваг, зазначених вище.
Паралельне ввімкнення ланок Паралельним з'єднанням ланок вважається таке, коли на вхід всіх ланок поступає одна і та ж величина, а вихідна величина рівна сумі вихідних величин окремих ланок. Математичну операцію сепарації – представлення відношення спектральної щільності сигналу і факторизованої спектральної щільності зашумленного сигналу з корінням в нижній напівплощині площини частоти у вигляді суми доданків і простого відкидання коріння нижньої напівплощини виконати значно складніше. Початкова електронна система представляється у вигляді паралельного сполучення більш простих складових з певними властивостями.
Ця операція приводить до фізично реалізовуваної системи управління, але розплатою за фізичну реалізацію є збільшення сталої помилки системи, яка мінімізується за визначенням. Існує два основні прийоми виконання вказаної операції: шляхом розкладання дробово-раціональної функції відношення спектральної щільності на суму простих множників (аналогічно розкладанню при інтегруванні дробово-раціональних функцій) або шляхом зворотного перетворень Лапласа вказаного співвідношення спектральної щільності, інтеграції в комплексній напівплощини параметра Р із застосуванням теореми Коші про вирахування, і прямого перетворення Лапласа сепарованого шляхом інтеграції виразу. Дрібно-раціональна функція це відношення двох багаточленів, які не мають спільних множників. Раціональні функції представляються в вигляді паралельного сполучення елементарних функцій, якщо порядок поліному чисельника дорівнює або менше полінома знаменника. Якщо навпаки, тоді виконується ділення для виділення цілої частини. В результаті отримують суму, яка складається з многочлена та правильної раціональної функції, де степінь чисельника менше ніж знаменника, а багаточлени не мають спільних множників. Розклад на простіші дроби тісне пов’язаний з розкладом знаменника на множники. Діленням чисельника і знаменника на коефіцієнт при старшому члені можна завжди досягти того, що коефіцієнт при старшому члені багаточлена знаменника дорівнює одиниці. За основною теоремою алгебри багаточлен знаменника можна розкласти на добуток двочленів з дійсними коренями та квадратних тричленів з дійсними та комплексно-спряженими коренями. Особливість полягає в тому що дійсні корені мають у чисельнику постійне число, а комплексно спряжені додатковий нуль. Одне та інше треба визначити. Найбільш поширений спосіб – метод невизначених коефіцієнтів. У першому випадку задача легко вирішувана, якщо елементарні поліноми мають перший порядок. У разі наявності періодичних складових порядок полінома рівний двом, коли коріння комплексно зв'язані – одне коріння знаходиться у верхній на півплощині, інше в нижній. В цьому випадку необхідно застосувати другий спосіб. Для цього знайдемо часову функцію відношення спектральної щільності, як зворотне перетворення Лапласа
Інтеграл уздовж нескінченної довжини уявної осі визначається інтегралом по замкнутому контуру, який складається з уявної осі і дуги півкола нескінченного радіусу. Тому інтеграл U(t) визначили як суму вирахувань зі всіма полюсами, що знаходяться в лівій і правій на півплощинах параметра р. Для часу t > 0 перетворення Лапласа відповідає правій на півплощині, що еквівалентно фізично нереалізовуваній системі і функція часу рівна нулю. Тому перетворення Лапласа виконали для функції часу
і одержали сепарований вираз, який має все полюси в лівій напівплощині і використовується у формулі (10.8)
Результати структурного синтезу оптимальних контурів управління по відхиленню і збуренню приведені в таблиці 7.2. Якщо корисний сигнал апроксимований поліномом другого порядку (процес без періодичної складової), то оптимальною структурою є інерційна ланка першого порядку. Для процесу з періодичною складовою (поліном четвертого порядку) оптимальна структура – форсована ланка другого порядку. Поліном шостого порядку приводить до дробово-раціональної функції, де порядок полінома знаменника рівний трьом, а чисельника – двом.
У загальному вигляді структура оптимальної по критерію мінімуму середньоквадратичної помилки передавальної функції замкнутої системи відтворення сигналу на фоні перешкоди є дробово-раціональною функцією, що поєднує два суперечливі процеси уповільнення і прискорення. Порядок полінома, прискорюючого (форсуючого) процес управління, на одиницю менше порядку характеристичного полінома уповільнюючого цей процес. Порядок уповільнюючого полінома рівний половині порядку характеристичного полінома спектральної щільності корисного (сумарного) сигналу. Одержані системи оптимальної швидкодії можна представлені у вигляді змінних стану. Змінні стану мають декілька іншу структуру, що пов'язане з особливостями побудови форсованих систем особливо для стохастичних вхідних сигналів.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 306; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.138.144 (0.014 с.) |
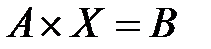 ,
,
 .
.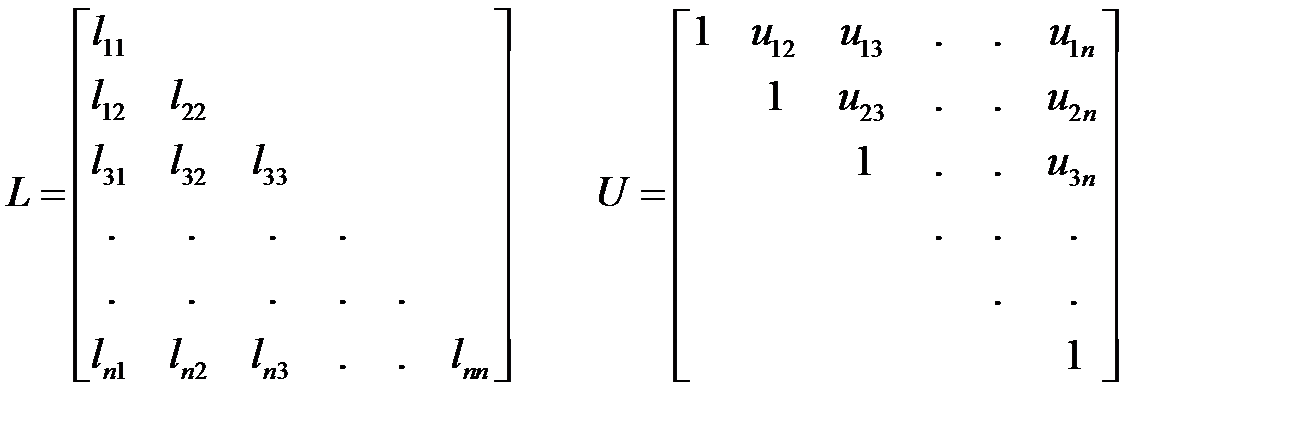
 i = 2, 3,..., n.
i = 2, 3,..., n. , i = n –1, n –2,..., 1.
, i = n –1, n –2,..., 1. , i = k, k +1,..., n,
, i = k, k +1,..., n, , j = k +1, k +2,..., n.
, j = k +1, k +2,..., n. .
.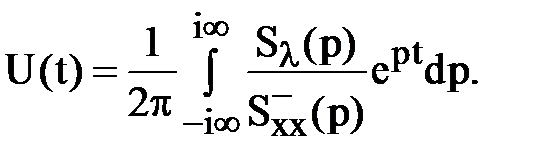
 ,
,



