
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы разложения и внесения под знак дифференциала.
Метод разложения Интеграл от лин комбин конечного числа инт ф-ий равен той же комбинации инт-лов от инт ф-ий Const множитель можно выносить за знак диф-ла Метов внесения под знак диф-ла
Замена переменной в неопределённом интеграле. Т. Пусть x?[a;b]
5.Метод интегрирования по частям.
Разложение рациональной функции на простые дроби. Первообразная любой рац ф-ии Интегрирование рациональных функций.
Первообразная любой рациональой функции Метод Остроградского метод выделения рациональной части неопределенного интеграла от рациональной дроби, знаменатель которой — многочлен степени n с кратными корнями, а числитель — многочлен степени m
Интегрирование некоторых тригонометрических выражений. a)
б)
в)
Интегрирование дробно-линейных иррациональностей.
Если Подстановки Эйлера
1) a>0: 2) c>0: 3) a<0, c<0, D>0, x1<x<x2: Выделение алгебраической части интеграла Ф-ия наз алгебраической, если в D(f) она обладает тождеству вида:pk(x)[f(x)]k+ pk-1(x)[f(x)]k-1+…+ p1(x)f(x)+ p0(x)=0, где n>=1, nєZ, pk, pk-1,…,p0,-некоторые многочлены, Pk(x)≠0. Подинтегральную ф-ию
Интегрирование дифференциальных биномов
1) p?Z Привести m и n к общ знаменателю λ(m=m’/ λ, n=n’/ λ)
2) (m +1)/n? Z
3) p+(m+1)/n? Z
Понятие определённого интеграла Римана. Необходимое условие интегрируемости. Опр Ф-ия f:[a;b]->R наз-ся инт-ой в смысле Римана на отрезке [a;b], если сущ конечный предел I интегральных сумм Условие: Если функция интегрируется в смысле Римана на отрезке, то она ограничена на этом отрезке. НО не всякая ф-ия, ограниченная на отрезке, интегрируема на нем в смысле Римана.
Суммы Дарбу и их св-ва Опр Нижней и верхней суммами Дарбу ф-ии f[a;b]->R, построенные для разбиения Т называются соответственно суммы Св-ва: 1)
2) При измельчении разбиения Т нижняя сумма только увеличивается, верхняя – только уменьшается 3) Нижняя сумма не превосходит верхней, даже если они построены для разных разбиений 4) Критерий Дарбу. Для интегрируемости ограниченной f[a;b]->R в смысле Римана на отрезке [a;b] ó чтобы выполнялось условие Интегрируемость непрерывной функции. Если функция непрерывна на отрезке, то она интегрируема на этом отрезке
Интегрируемость монотонной на отрезке функции Если функция монотонна на отрезке, то она интегрируема на этом отрезке Понятие о критерии Лебега. Опр. Покрытие мн-ва Е – семейство мн-ва Опр. Мн-во счётное, если можно установить взаимооднознач соотношение между его элементами Опр. Мн-во ЕcR имеет лебегову меру ноль, если Т. Для того, чтобы огр ф-ия f:[a;b]->R была инт-ма в смысле Римана ó чтобы мн-во всех её точек имело лебегову меру ноль. Сл-вие Ф-ия, имеющая на отрезке конечное мн-во точек разрыва инт-ма в смысле Римана на это отрезке
Сл-вие Изменение значений ф-ии f:[a;b]->R на конечном мн-ве точек не влияет ни на инт-ость ф-ии, ни на величину
|
||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 210; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.143.4 (0.009 с.) |

 и отобр
и отобр  – диф-ема и биективна. Тогда
– диф-ема и биективна. Тогда  , где
, где 
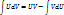
 выражается через рац ф-ии, а также ln и arctg. Рац часть первообразной, будучи приведена к общему знаменателю, должна в качестве такового иметь произведение всех сомножителей, на которые раскладывается многочлен Q(x), только с кратностями, на единицу меньшими, чем кратность их вхождения в разложение Q(x).
выражается через рац ф-ии, а также ln и arctg. Рац часть первообразной, будучи приведена к общему знаменателю, должна в качестве такового иметь произведение всех сомножителей, на которые раскладывается многочлен Q(x), только с кратностями, на единицу меньшими, чем кратность их вхождения в разложение Q(x). , где
, где
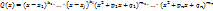
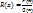 выражается через рациональные функции, а также трнсцендентные функции
выражается через рациональные функции, а также трнсцендентные функции  и
и  .
. n-1. Согласно этому методу,
n-1. Согласно этому методу,  , где многочлены Q1, Q2, P1, P2 имеют степени соответственно n1, n2, m1, m2, такие что n1 + n2 = n, m1
, где многочлены Q1, Q2, P1, P2 имеют степени соответственно n1, n2, m1, m2, такие что n1 + n2 = n, m1  , следовательно, его можно найти, используя алгоритм Евклида. Из этого равенства, дифференцируя, получаем тождество, которое позволяет найти явное выражение многочленов P1(x) и P2(x).
, следовательно, его можно найти, используя алгоритм Евклида. Из этого равенства, дифференцируя, получаем тождество, которое позволяет найти явное выражение многочленов P1(x) и P2(x).  :
:
 или
или  где
где  – рациональная функция:
– рациональная функция: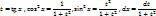
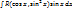 или
или 
 или
или  :
:  и
и 

 , то
, то  ,
, 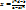 , y=t.
, y=t.



 алгебр преобраз всегда можно представить в виде суммы:R1(x)/
алгебр преобраз всегда можно представить в виде суммы:R1(x)/  +R2(x), где R1(x), R2(x) –рац ф-ии.∫ R(x,
+R2(x), где R1(x), R2(x) –рац ф-ии.∫ R(x,  dx. Разложив рац R1(x) на сумму многочленов pr(x) элем-ных дробей приходим к инт-лам след 3х видов:а)∫Pr(x)/
dx. Разложив рац R1(x) на сумму многочленов pr(x) элем-ных дробей приходим к инт-лам след 3х видов:а)∫Pr(x)/  dx; б)∫1/((x-α)k
dx; б)∫1/((x-α)k 
 Это инт-л от др-лин иррац => далее t=
Это инт-л от др-лин иррац => далее t= 

 , λ – знаменатель p.
, λ – знаменатель p. 
 . λ – знаменатель p.
. λ – знаменатель p. 
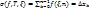 при
при  , т.е.
, т.е.  . Этот предел наз-ся инт-лом Римана для f на [a;b] и обозн
. Этот предел наз-ся инт-лом Римана для f на [a;b] и обозн 




 (эти числа – верхн и нижн инт-лы от f[a;b]->R)
(эти числа – верхн и нижн инт-лы от f[a;b]->R) или что тоже самое
или что тоже самое  где
где  - колебание функции на отрезке
- колебание функции на отрезке 
 , что EcV, т.е.
, что EcV, т.е. 
 такое покрытие мн-ва Е с конечным или счётным семейством интервалов, что сумма длин любого кол-ва интервалов
такое покрытие мн-ва Е с конечным или счётным семейством интервалов, что сумма длин любого кол-ва интервалов 



